三峡库区石榴树包滑坡近期变形特征与机理分析

杨何; 汤明高; 许强; 龚正峰; 祝权

doi:10.16031/j.cnki.issn.1003-8035.2022.01-08

三峡库区石榴树包滑坡近期变形特征与机理分析

杨何^1,,
汤明高^2, ,,
许强²,
龚正峰²,
祝权²

1.
成都大学建筑与土木工程学院, 四川成都　610106
2.
成都理工大学地质灾害防治与地质环境保护国家重点实验室, 四川成都　610059

基金项目: 国家自然科学基金面上项目(41977255)；国家重点研发计划资助项目(2018YFC1505105)；三峡后续工作地质灾害防治研究(000121 2015C C60 005)

详细信息

作者简介:
杨　何(1985-)，男，四川射洪人，博士，高级工程师，主要从事地质灾害评价与预测方向的研究。E-mail：yanghexq@163.com

通讯作者:
汤明高(1978-)，男，湖北仙桃人，博士，教授，主要从事工程地质与岩土工程教学科研。E-mail：tomyr2008@163.com

中图分类号: P642.2
计量
- 文章访问数: 364
- HTML全文浏览量: 212
- PDF下载量: 257
出版历程
- 收稿日期: 2020-08-24
- 修回日期: 2021-10-02
- 网络出版日期: 2022-01-27
- 刊出日期: 2022-03-06

Recent deformation characteristics and mechanism of the Shiliushubao landslide in the Three Gorges Reservoir Area

1.
School of Architecture and Civil Engineering, Chengdu University, Chengdu, Sichuan　610106, China
2.
State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu, Sichuan　610059, China

摘要

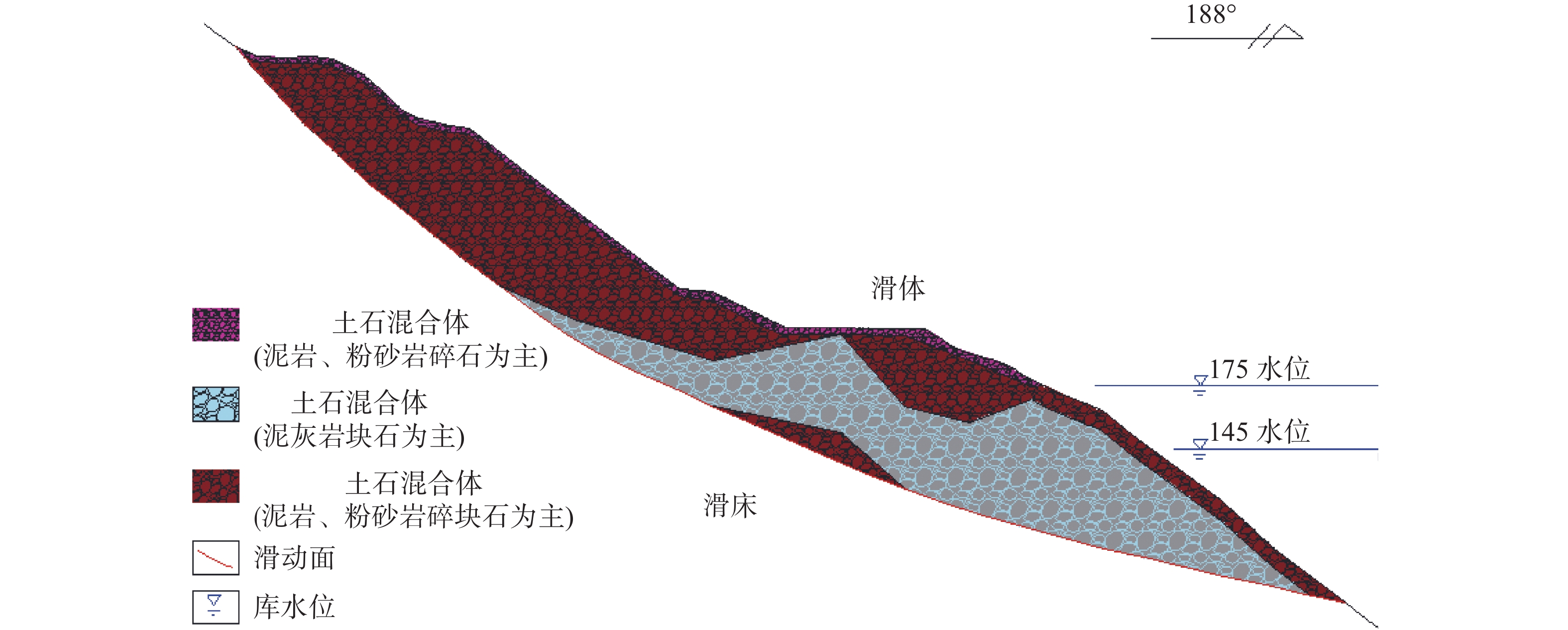
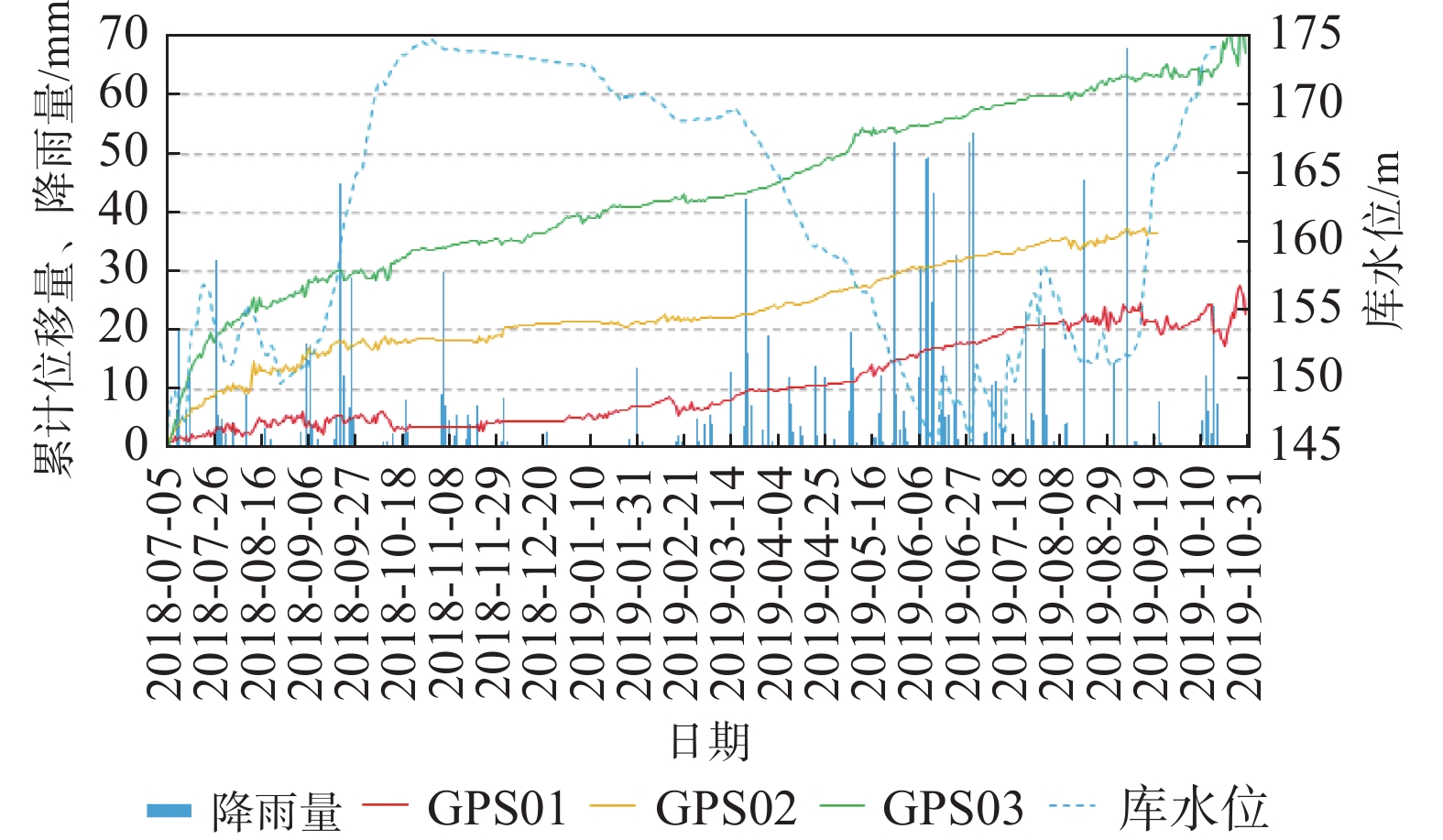
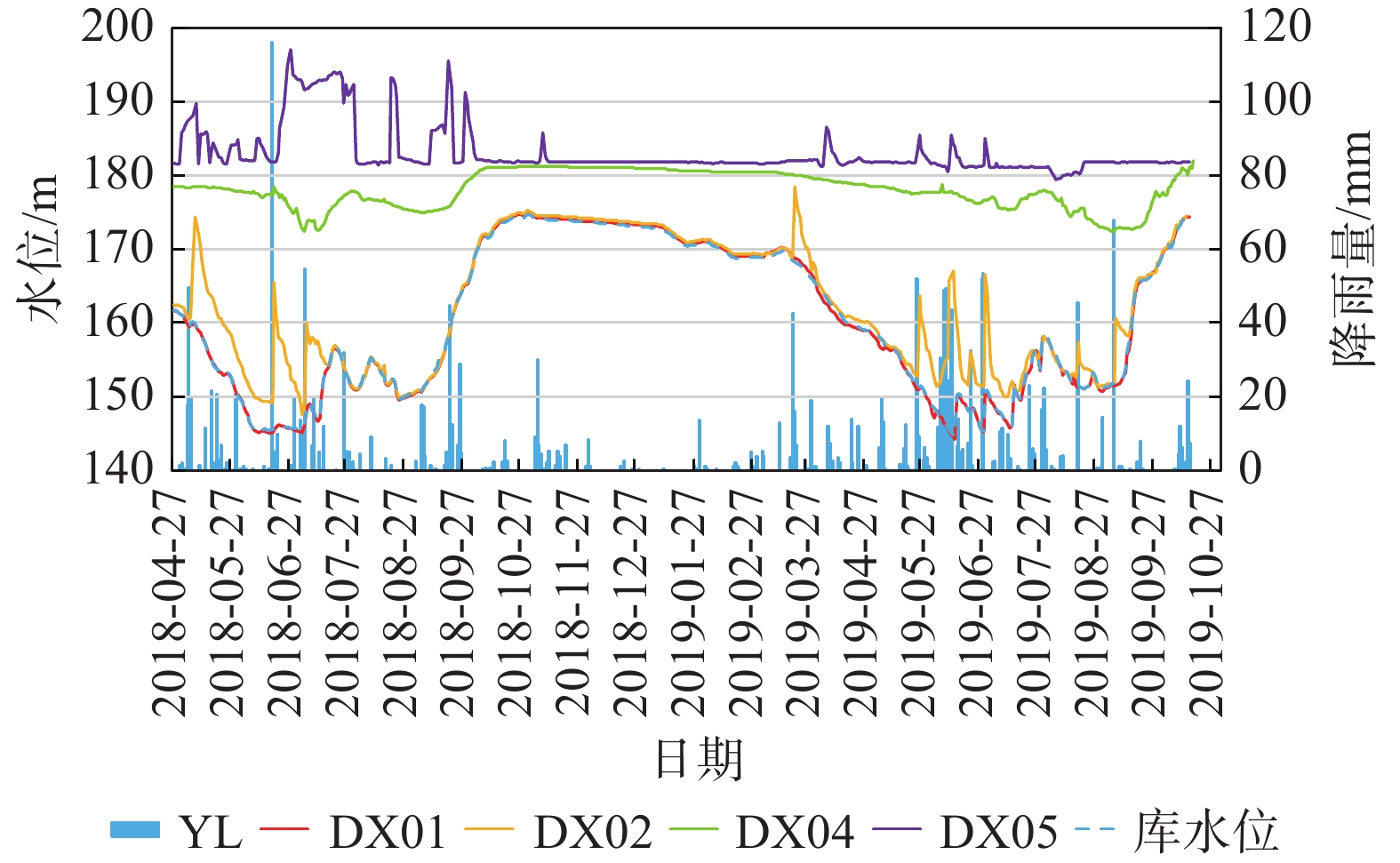
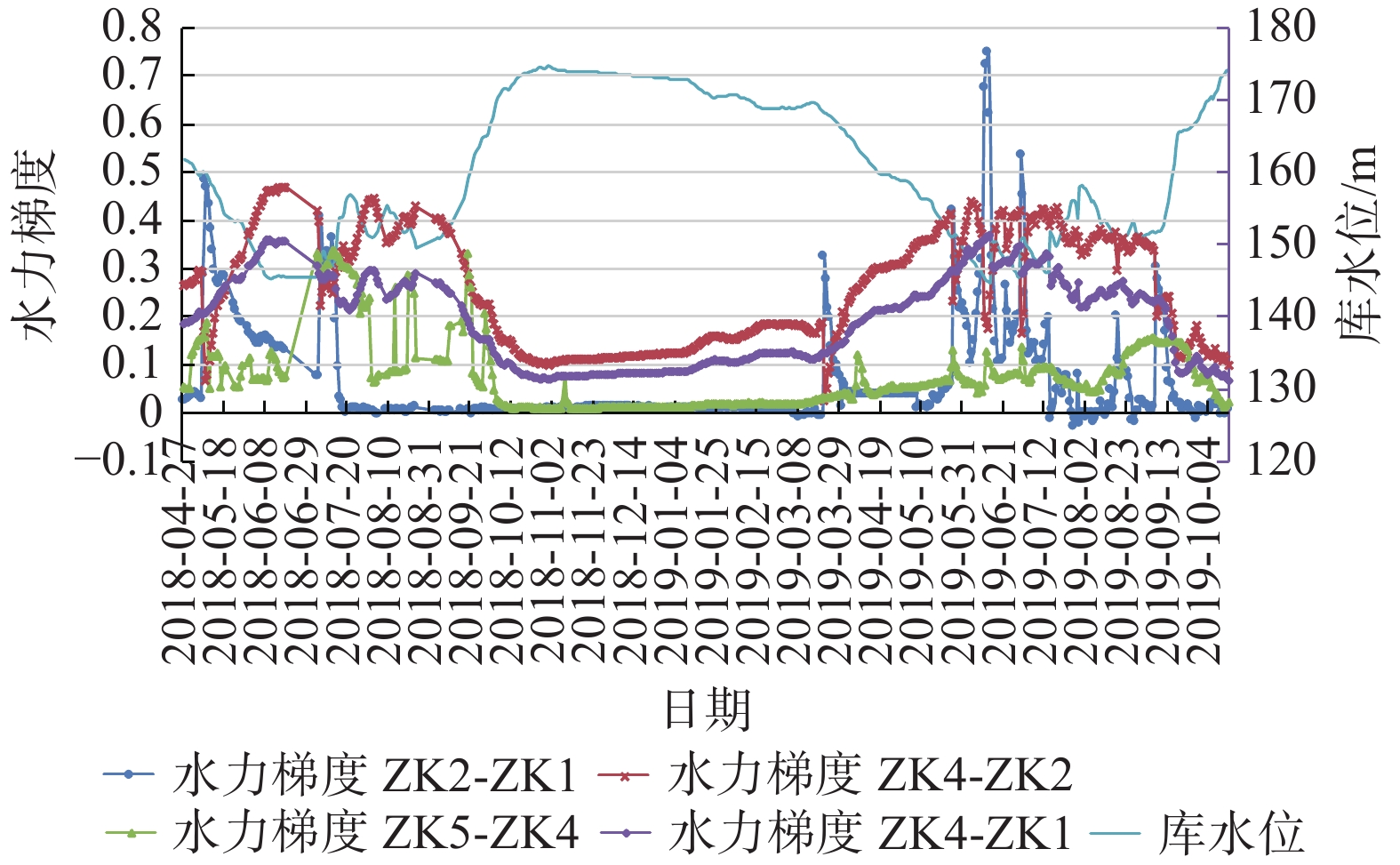
摘要: 石榴树包滑坡是黄蜡石滑坡群中的一个重要滑坡，一直以来备受瞩目，其持续变形对长江航运及人民生命财产安全造成严重威胁。本文通过对石榴树包滑坡的勘探得到其详细的物质组成及结构，通过近两年的GPS表面位移、地下水位、降雨量等自动化监测数据分析，对该滑坡的变形特征、变形机理进行研究。结果表明：（1）石榴树包滑坡最初以前缘变形为主，现阶段以中后部变形为主。（2）降雨是石榴树包滑坡复活的主要原因，受库水位升降与降雨联合作用使石榴树包滑坡持续变形。前缘变形较小主要是由于前缘渗透性大，水力梯度较小的原因；中后部变形大主要是中后部渗透性小，水力梯度相对较大的原因。（3）降雨对滑坡地下水影响较大，使地下水水力梯度增大可达5～9倍。本研究可为三峡库区滑坡灾害监测预警及防治提供重要参考。
- 三峡库区 /
- 滑坡 /
- 变形特征 /
- 变形机制 /
- 水力梯度
Abstract: Shiliushubao landslide is an important part of the Huanglashi landslide group, which has attracted much attention for a long time. In this paper, the detailed material composition and structure of the Shiliushubao landslide are obtained by the exploration, and the deformation characteristics and deformation mechanism of the landslide are studied through automatic GPS surface displacement, groundwater level, rainfall monitoring in recent two years. The results show that the front deformation is the main deformation of the Shiliushubao landslide at first, and at present, the deformation of the middle and rear part is the main deformation. Rainfall is the main reason for the reactivation of Shiliushubao landslide, which is continuously deformed by the joint action of reservoir water level rise and fall and rainfall. The small deformation of the leading edge is mainly due to the high permeability of the front edge and the small hydraulic gradient; the large deformation of the middle and rear part is mainly due to the small permeability of the middle and rear part and the relatively large hydraulic gradient. Rainfall has a great influence on the groundwater of landslide, which makes the hydraulic gradient of groundwater increase 5～9 times. This study can provide an important reference for monitoring - early warning and prevention of landslide in the Three Gorges Reservoir area.
- Three Gorges Reservoir Area /
- landslide /
- deformation characteristic /
- deformation mechanism /
- hydraulic gradient

HTML全文

0. 引言

我国地处世界最大的陆、海板块交界处^[1]，地震活动频繁，其危害程度在全球位居首位^{[2 − 3]}。地震引发的滑坡、泥石流等次生灾害，常导致建筑和基础设施严重受损，以及众多人员伤亡^{[4 − 7]}。以2008年汶川8.0级地震为例，该地震诱发了众多山体滑坡，致使超过2.2万人丧生，占地震总死亡人数的33%左右^{[8 − 11]}。鉴于此，对地震引发的边坡稳定性进行评估显得尤为关键。

目前，定量评估地震边坡稳定性的最常用方法是拟静力法^{[12 − 14]}，该方法通常与极限平衡法并用，以评估地震对边坡稳定性的影响^{[15 − 16]}。拟静力法是一种用于分析结构在地震作用下响应的简化方法，该方法将地震力简化为一个等效的静力荷载^[17]，然后按照静力分析的方法来计算结构的动力响应。由于概念清晰、计算简单、能够快速评估给出结构在地震作用下的响应评估，已被纳入众多行业规范^[18]。然而，随着拟静力法的广泛应用，地震系数的不同取值将直接影响评估结果。因此，确定合适的地震系数取值成为拟静力法中的核心问题。

关于地震系数的取值，有不少学者做了大量相关工作。1950年，Terzaghi等^[17]提出了不同级别地震对应的水平地震系数，分别为0.1、0.2、0.5，对应于“强烈性”、“破坏性”、“灾害性”地震；1981年，Marcuson等^[19]提出，若边坡安全系数超过1，则拟静力水平地震系数应取基岩峰值加速度的1/3至1/2；Hynes-Griffin等^[20]建议，在边坡稳定性安全系数超过1的情况下，水平地震系数应为基岩峰值加速度的1/2；Baker等^[21]则提出将基岩峰值加速度的3/4作为地震系数。Seed等^[22]建议，当安全系数超过1.15时，水平地震系数应在0.1至0.2之间选取。这些地震系数的确定主要基于两种思路：一种是Terzaghi等人依据震级提出的，但这种方法随着距离震源的增大，其适用性会减弱；另一种是基于区域地震烈度，更贴近实际情况。但这两种方法给出的地震系数取值并不一致，并且关于地震系数的确定方法，还未形成统一的理论公式。因此，深入研究地震系数的取值及其确定方法显得格外重要

本文利用剪切梁理论，推导出直角梯形边坡在地震作用下的加速度响应公式；深入分析了多种因素对地震动放大系数的作用；构建了Rg与PGA的关联表达式；进一步得到了地震系数的取值公式，并明确了不同地震烈度下的地震系数具体数值；提出了一种理论公式和统计方法相结合的计算方法，为直角梯形边坡地震系数的确定提供了坚实的理论支持。

1. 基于剪切梁法的边坡响应加速度公式推导

1.1 剪切梁法的基本原理及公式推导

剪切梁理论将土体结构当作一系列串联的剪切弹簧和阻尼装置，形成一个连续的薄层振动模型（图1）。在地震引发的横向剪切震动作用下，该理论采用二维应力状态对土体进行解析研究^[23]。Mononobe^[24]、Gazetas^[25]、Dakoulas^[26]等学者曾利用有限元法验证了此方法用于大坝地震动力响应分析的合理性，本文旨在利用剪切梁计算边坡地震系数的研究，故不在此做验证工作。剪切梁法的基本假设如下：

图 1 二维边坡剪切梁模型

Figure 1. Two-dimensional slope shear beam model

下载: 全尺寸图片幻灯片

（1）边坡为无限长的直角梯形断面，坡体嵌固在刚性地基上；

（2）土体为各向同性体；

（3）边坡的宽高比（B/H）很大，仅考虑横向地震作用下的剪力，忽略弯矩的影响。

在图1所示中，G指剪切模量，ρ代表材料密度，c表示阻尼系数，B是边坡顶端宽度， α为坡角，β指的是边坡顶端与垂直线的夹角，H为坡高，h为计算深度， ${\ddot{u}}_{g}$ 为地震波加速度时程曲线。

在边坡的地震响应分析中，采用的剪切梁模型与图1所示相同，取一微小单元进行受力分析（图2），当考虑阻尼及地震荷载作用下，得到的平衡方程为：

图 2 剪切梁微元示意图

Figure 2. Schematic diagram of a shear beam microelement

下载: 全尺寸图片幻灯片

\frac{\partial^{2} u}{{\partial t}^{2}} - \frac{G}{ρ} [\frac{\partial^{2} u}{{\partial t}^{2}} + \frac{1}{B / \tan β + z} \frac{\partial u}{\partial z}] + \frac{c}{ρ} \frac{\partial u}{\partial t} = - {\overset{⃛}{u}}_{g}

(1)

求解得到边坡在地震作用下的相对于地面的位移公式：

\begin{aligned} u = & - \sum_{i = 1}^{\infty} \frac{2 J_{0} [β_{0 i} \frac{B / \tan β + z}{B / \tan β + H}]}{β_{0 i} J_{1} (β_{0 i}) ω_{0}} \int_{0}^{t} e^{- λ ω （ t - τ ）} \frac{d^{2} u_{g}}{d t^{2}} \sin [ω_{0} (t - \\ τ)] d τ \end{aligned}

(2)

对上式求二阶导数，得到边坡相对于地面的加速度：

\begin{aligned} \frac{d^{2} u_{a}}{d t^{2}} = & \sum_{i = 1}^{\infty} \frac{2 ω J_{0} [β_{0 i} \frac{B / t a n (90 - α) + z}{B / \tan (90 - α) + H}]}{β_{0 i} J_{1} (β_{0 i})} \int_{0}^{t} e^{- λ ω (t - τ)} \cdot \\ \frac{d^{2} u_{g}}{d t^{2}} \sin [ω_{0} (t - τ)] d τ \end{aligned}

(3)

式中：J₀、J₁——0、1阶贝塞尔函数；

β_0ι——零阶贝塞尔函数的根，其中前5个根为 2.4048、5.5201、8.6537、11.7915、14.9309；

ω——边坡的固定角频率， $ω = ω_{0} \sqrt{1 - λ^{2}}$ ；

$λ$ ——边坡的阻尼比；

${\ddot{u}}_{g}$ ——地震加速度；

α——坡角（α =90°− β）。

1.2 地震动数据处理及分类

在PEER Ground Motion Database随机收集了435条地震动加速度时程数据，后进行滤波（0～15 Hz）与基线校正，将处理后的地震动数据按照PGA大小进行分类。具体分类为：PGA小于等于0.05g视为Ⅰ区、0.05g～0.1g（包括0.1g）之间视为Ⅱ区、0.1g～0.2g（包括0.2g）视为Ⅲ区、0.2g～0.4g（包括0.4g）视为Ⅳ区、大于0.4g视为Ⅴ区（表1）。

表 1 PGA与烈度对应关系及地震波基本信息表

Table 1. Correspondence between PGA and intensity and basic information on seismic waves

PGA/g	≤0.05	（0.05,0.1]	（0.1,0.2]	（0.2,0.4]	＞0.4
区域	Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ
数量/条	163	82	117	52	21
PGA_max/g	0.04934	0.09949	0.2	0.39481	1.23307
PGA_min/g	0.0029	0.05077	0.10155	0.20021	0.40112
平均PGA/g	0.03	0.072	0.143	0.298	0.647
平均卓越周期/s	0.481	0.41	0.241	0.221	0.238
平均卓越频率/Hz	2.08	2.4	4.149	4.52	4.2
注：PGA_max、PGA_min分别为所划分区域的地震动数据PGA的最大值与最小值。

下载: 导出CSV

| 显示表格

数据显示，在5个不同区域Ⅰ至Ⅴ中，分别记录到163、82、117、52和21次地震动信息，这些区域对应的地面峰值加速度（PGA）均值依次为0.03g、0.072g、0.143g、0.298g和0.647g。PGA的极值范围在0.0029g至1.23307g之间。地震波的卓越频率集中在2～4 Hz，而卓越周期的均值介于0.2～0.5 s。在PGA值较小的情况下，地震波呈现出较长的卓越周期和较低的卓越频率；而在PGA值较大的情况下，则表现出较短的卓越周期和较高的卓越频率。

2. 地震边坡的动力响应特征分析

为直观、简单的表示各因素的对边坡响应加速度的影响，定义边坡地震峰值响应加速度（peak respond acceleration，PRA）和输入地震动峰值加速度（Peak Ground Acceleration，PGA）的绝对值之比为Rg，见式（4）。

R g = \frac{P R A}{P G A} = \frac{| max {\frac{d^{2} u_{a}}{d t^{2}}} |}{| max {\frac{d^{2} u_{g}}{d t^{2}}} |} = \frac{| max {\sum_{i = 1}^{\infty} \frac{2 ω J_{0} [β_{0 i} \frac{B / \tan (90 - α) + z}{B / \tan (90 - α) + H}]}{β_{0 i} J_{1} (β_{0 i})} \int_{0}^{t} e^{- λ ω (t - τ)} \frac{d^{2} u_{g}}{d t^{2}} \sin [ω_{0} (t - τ)] d τ} |}{| max {\frac{d^{2} u_{g}}{d t^{2}}} |}

(4)

由上式可知，Rg体现了输入地震波在坡体内传播之后所产生的放大效应。本文的计算工况及参数见表2，边坡的密度统一取1794.1 kg/m^3[26]。

表 2 计算参数汇总表

Table 2. Summary table of calculation parameters

H/m	B/m	α/（°）	阻尼比	E/MPa
5/10/15/20/25/ 30/35/40/45/50	70	30	0.1	15
15	70	20/30/40/50/60/70	0.1	15
15	70	30	0.1/0.15/0.2/0.25/0.3	15
15	70	30	0.1	3～25

下载: 导出CSV

| 显示表格

2.1 输入地震动峰值加速度（PGA）

选取Kobe地震波，将放大因子分别调整为0.5、1.0、1.5、2.0，以获得不同PGA大小而频率相同的地震波。PGA与PRA的关系如图3所示。PRA的大小与输入地震动PGA大小关系为同增同减，且变化相同的倍数，说明PRA会随着PGA的改变而改变，但两者的比值Rg始终为一定值，为0.9412。因此，不同大小的PGA会产生不同大小的PRA；PGA越大，所产生的PRA也越大，边坡所受的地震力也越大，所对应的地震系数也越大。

图 3 不同PGA放大因子下边坡响应加速度曲线图

Figure 3. Acceleration curves of slope response under different PGA amplification factors

下载: 全尺寸图片幻灯片

2.2 边坡材料特性

2.2.1 弹性模量

言志信^[27]研究表明，在边坡几何参数不变的情况下，其频率主要受其边坡弹性模量的影响，并与其固有频率成正比，不同几何形态边坡的固有频率计算公式如下式（5）。本文在分析不同几何尺寸的边坡动力响应时，均采用了式（5）所计算的结果。

f = \frac{E^{0.5} \cdot θ^{0.277}}{e^{3.432} \cdot h \cdot ρ^{0.497}}

(5)

式中：f——边坡的固有频率/Hz；

θ——边坡的坡角/（°）；

E——弹性模量/Pa；

h——坡高/m；

ρ——材料密度/（kg·m⁻³）；

e——自然指数。

边坡弹性模量对Rg的影响如图4所示（图中频率由弹性模量计算得到），所采用的地震波信息如表3所示。结果显示，Rg的峰值是由地震波的卓越频率所决定的，在其左右两侧，总体上呈现出一种先升高、后降低的趋势。倘若边坡固有频率和地震波的卓越频率相近，那么就会发生“同频共振”效应，相应的地震力达到最大值。

图 4 Rg随弹性模量变化图

Figure 4. Variation of Rg with elastic modulus

下载: 全尺寸图片幻灯片

表 3 地震波信息表

Table 3. Seismic wave information table

地震名称	卓越周期/s	卓越频率/Hz
1995年日本神户地震	0.16	6.25
1992年美国兰德斯地震	0.08	12.5
1999年台湾集集地震	0.12	8.3

下载: 导出CSV

| 显示表格

2.2.2 阻尼比

如图5所示，随着阻尼比的增加，Rg逐步降低。这是由于阻尼比的增加有助于高效吸收地震波在边坡介质中传递的动能。当边坡的阻尼比较高时，它能显著减少地震引发的震动幅度，此时边坡在阻尼比影响下所消耗的能量增多，进而导致在地震影响下边坡的峰值加速度减小。

图 5 Rg随阻尼比变化图

Figure 5. Variation of Rg with damping ratio

下载: 全尺寸图片幻灯片

2.3 边坡几何特性

图6、7结果分别显示Rg随坡高与坡角的变化关系。

图 6 Rg随坡高变化图

Figure 6. Variation of Rg with slope height

下载: 全尺寸图片幻灯片

图 7 Rg随坡角变化图

Figure 7. Variation of Rg with slope angle

下载: 全尺寸图片幻灯片

在分析中发现Rg与坡高之间存在一种负相关关系。起初，坡高增大，Rg的减少速度很快，曲线的倾斜度非常明显；然而，随着坡高的进一步增加，Rg的减少速度逐渐减慢，曲线的倾斜度变得平缓。可以发现，当坡高无限增加时，Rg趋向于0，说明高位和极高位边坡不适合利用剪切梁法来计算地震系数。同时，由于剪切梁法是将地震力作为剪切力来（类似于地震波的横波），横波作用下的低层构筑物响应大于高层构筑物。此外，Rg与坡度角呈正相关性。与坡高相反，Rg随坡角增大而增加，这是因为起初，小坡角边坡的卓越频率远小于地震波的卓越频率，边坡响应加速度较小；随着坡角的增大，边坡的固有振动频率逐渐接近地震波的卓越频率，从而使得边坡的加速度响应增强。

3. 拟静力法中的地震系数取值

地震边坡稳定性分析中拟静力法的基本原理如图8所示，Kramer将拟静力法中边坡所受的地震力概括为地震系数与滑块质量的乘积^[28]，见式（6）。

图 8 简化边坡模型的拟静力法原理图

Figure 8. Schematic diagram of the pseudo-static method for a simplified slope model

下载: 全尺寸图片幻灯片

{\begin{matrix} F_{h} = \frac{a_{h} w}{g} = k_{h} w \\ F_{v} = \frac{a_{v} w}{g} = k_{v} w \end{matrix}

(6)

式中： $F_{h} 、 F_{v}$ ——水平、竖直地震力；

$a_{h} 、 a_{v}$ ——水平、竖直拟静力加速度；

$w$ ——滑体的重量；

$k_{h} 、 k_{v}$ ——水平、竖直地震系数。

根据上述地震系数的定义以及本文的研究，因此可用边坡的PRA（Rg与PGA的乘积）作为地震系数的取值依据。地震系数的选取应满足一般基本工程的需求，这就要求所取的地震系数具有广泛性以及合理性。第2部分讨论了边坡几何特性、材料特性、输入地震动PGA对Rg的影响，为满足地震系数的广泛性及合理性，应按最不利因素考虑原则，使边坡的响应加速度达到最大值。然而，地震波是客观存在的，无法预先得知地震动有关参数，因此边坡响应加速度大小可归因于边坡固有频率的影响。根据以上分析结果，最终选择坡高为5 m、坡角为70°、坡宽为70 m、阻尼比为0.1、边坡弹性模量取15 MPa、密度为1794.1 kg/m³作为最终的计算参数（确定边坡的几何形态后，用此弹性模量计算得到固有频率接近地震波的卓越频率）。此方法得到的地震系数仅为理论解，不考虑此参数的边坡模型与野外实际边坡几何形状之间的差异。

435条地震动数据在上述参数下的计算结果如图9所示。计算结果得到Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ区的平均Rg值分别为1.714、1.586、1.266、1.133、1.139，总体上Rg随PGA的增大而减小。然而，鉴于图9 中各个区域的 PGA 平均值并未达到地震烈度分别为 Ⅵ、Ⅶ、Ⅷ、Ⅸ 区所对应的设计基本加速度值（0.05g、0.1g、0.2g、0.4g），需将图中Rg与PGA两者的平均值进行非线性拟合，用拟合函数计算当地震烈度为Ⅵ、Ⅶ、Ⅷ、Ⅸ时，其设计基本加速度值所对应的Rg值。

图 9 Rg与PGA关系图

Figure 9. Plot of Rg versus PGA

下载: 全尺寸图片幻灯片

图10为Rg平均值与PGA的拟合曲线，所对应的拟合方程为式（7）。拟合所得到的相关系数（R²）是 0.94469（大于 0.9），能够利用拟合函数去计算未知点的函数值。

图 10 Rg与PGA关系曲线拟合图

Figure 10. Rg versus PGA curve fitting plot

下载: 全尺寸图片幻灯片

R g = 0.858 0 e^{- \frac{P G A}{0.096 48}} + 1.113 49

(7)

将PGA分别为0.05g、0.1g、0.2g、0.4g带入式7中计算所对应的Rg值，计算结果如表4所示。从表4可以看出地震烈度为Ⅵ、Ⅶ、Ⅷ、Ⅸ区所对应的Rg分别为1.62、1.42、1.22、1.13，所对应的地震系数取值分别为0.04、0.07、0.11、0.21。表4中的地震系数是综合影响系数0.45、PGA、Rg三者的乘积与重力加速度的比值，可用式（8）来表示地震系数的取值公式（其中PGA的单位为g）。其中综合影响系数是考虑结算结果与宏观震害之间差异的影响^[29]，即在边坡响应加速度最大值的一瞬间，边坡可能不会立刻产生破坏。本文采用的综合影响系数是边坡响应加速度时程中，阿里亚斯强度为5%～95%之间所对应的有效时间内，边坡响应加速度的平均值与PRA比值的统计值，图11为综合影响系数的物理参数示意图。

表 4 地震系数建议取值表

Table 4. Table of recommended values for seismic coefficients

地震烈度	Ⅵ	Ⅶ	Ⅷ	Ⅸ
PGA/g	0.05	0.10	0.20	0.40
Rg	1.62	1.42	1.22	1.13
地震系数	0.04	0.07	0.11	0.21

下载: 导出CSV

| 显示表格

图 11 综合影响系数物理示意图

Figure 11. Physical schematic diagram of the comprehensive impact coefficient

下载: 全尺寸图片幻灯片

k = (0.45 \cdot R g \cdot P G A) / g

(8)

4. 讨论

将本文得出的地震系数与前人研究成果对比如表5所示。本文地震系数与Marcuson等^[24]、 Hynes-Griffin等^[20]、 Baker等^[21]等学者提出的地震系数规律一致，随着烈度的增加而增加，基本上烈度增加一度，地震系数的取值几乎增加一倍，且取值整体上小于Terzaghi^[18]、 Seed^[22]等人提出以震级为依据的地震系数取值。图12结果显示本文的计算结果大于Marcuson等^[24]、 Hynes-Griffin等^[20]所给出的地震系数；小于Baker等^[21]提出的地震系数。其中与Hynes-Griffin等^[20]、Marcuson等^[24]地震系数上限接近。本文给出的地震系数值分别为Ⅵ、Ⅶ、Ⅷ、Ⅸ区设计基本加速度的0.8、0.7、0.55、0.525倍，Ⅵ、Ⅶ区整体上大于Marcuson等^[24]、Hynes-Griffin等^[20]、Baker等^[21]学者给出的取基岩峰值加速度的1/3～1/2、1/2、3/4，Ⅷ、Ⅸ区基本上差别不大。总体而言：本文得到的地震系数与前人给出的地震系数相对吻合，具有一定的参考价值。

表 5 地震系数对比表

Table 5. Comparison table of seismic coefficients

来源	取值依据和条件	地震系数
Terzaghi^[18]	地震震级	对于“严重”“破坏性”和“灾难性”地震，水平地震系数分别为0.1、0.2和0.5
Seed^[22]	地震震级且安全系数F_s > 1.15	当震级M=6.5时，k=0.1；当震级M=8.5时，k=0.2
Hynes-Griffin^[20]	地震烈度且安全系数F_s > 1	Ⅵ：0.025、Ⅶ：0.05、Ⅷ：0.1、Ⅸ：0.2
Marcuson^[24]	地震烈度且安全系数F_s > 1	Ⅵ：0.017～0.025、Ⅶ：0.03～0.05、Ⅷ：0.06～0.1、Ⅸ：0.13～0.2
Baker^[21]	地震烈度	Ⅵ：0.0375、Ⅶ：0.075、Ⅷ：0.15、Ⅸ：0.3
本文计算结果	地震烈度	Ⅵ：0.04、Ⅶ：0.07、Ⅷ：0.11、Ⅸ：0.21

下载: 导出CSV

| 显示表格

图 12 地震系数对比图

Figure 12. Comparison diagram of seismic coefficients

下载: 全尺寸图片幻灯片

迄今为止，虽然在评价地震边坡稳定性分析方面有更加合理的拟动力、Newmark等方法。然而，由于拟静力法的物理概念明晰，计算方式较为简便，计算工作量较小，而且积累了丰富的使用经验，仍是工程界分析地震边坡稳定性分析的最常用方法。作者受前人工作的启发，利用剪切梁理论来分析边坡的动力响应特征，旨在探求一种求解地震系数的理论方法，为促进相关领域的发展贡献出自身力所能及的力量。

本文提出的方法也存在一定的局限性，例如将边坡简化为平面应变问题并不符合实际，现实边坡并非是二维均质与各向同性的；只从总体上简单考虑了频谱信息，并没有深入讨论频谱对边坡动力响应的影响；综合影响系数的取值只进行了统计，并没有从相关理论上验证其取值的合理性。针对本文方法的不足之处，后续还需进一步研究，将拟静力法中地震系数的取值更为精确，用于解决实际的工程问题。

5. 结论

（1）边坡高度、阻尼比与Rg值呈现反比关系；斜坡角度与Rg值则呈现正比关系；而PGA会影响PRA，对Rg无影响，对于Kobe地震波，Rg比值始终为0.9412；

（2）拟合得到边坡动力放大系数与地震输入峰值加速度之间的关系式。确定地震烈度为Ⅵ、Ⅶ、Ⅷ、Ⅸ度时，推荐相应的地震系数分别为0.04、0.07、0.11、0.21。

图 1 石榴树包滑坡遥感图

Figure 1. Remote sensing map of Shiliushubao landslide

下载: 全尺寸图片幻灯片

图 2 石榴树包滑坡边界特征

Figure 2. Boundary characteristics of Shiliushubao landslide

下载: 全尺寸图片幻灯片

图 3 石榴树包滑坡勘探及监测仪器布置图

Figure 3. Layout of exploration and monitoring instruments for Shiliushubao landslide

下载: 全尺寸图片幻灯片

图 4 石榴树包滑坡钻孔岩芯

Figure 4. Borehole core of Shiliushubao landslide

下载: 全尺寸图片幻灯片

图 5 石榴树包滑坡工程地质纵剖面

Figure 5. Engineering geological profile of Shiliushubao landslide

下载: 全尺寸图片幻灯片

图 6 石榴树包滑坡电法测量结果与钻孔岩心对比

Figure 6. Comparison of electrical survey results and borehole cores of Shiliushubao landslide

下载: 全尺寸图片幻灯片

图 7 石榴树包滑坡体纵剖面物质结构分层

Figure 7. Material structure stratification of longitudinal section of Shiliushubao landslide body

下载: 全尺寸图片幻灯片

图 8 石榴树包滑坡GPS监测累计位移量-雨量-库水位变化曲线

Figure 8. Variation curve of cumulative displacement of GPS monitoring and rainfall and reservoir water level of Shiliushubao landslide

下载: 全尺寸图片幻灯片

图 9 石榴树包滑坡地下水位变化曲线

Figure 9. Variation curve of groundwater level in Shiliushubao landslide

下载: 全尺寸图片幻灯片

图 10 石榴树包滑坡水力梯度变化曲线

Figure 10. Variation curve of hydraulic gradient of Shiliushubao landslide

下载: 全尺寸图片幻灯片

表 1 水力梯度变化特征

Table 1 Variation characteristics of hydraulic gradient

项目	水力梯度i₂₋₁			水力梯度i₄₋₂			水力梯度i₅₋₄
项目	高水位时	低水位时	降雨时	高水位	低水位	降雨时	高水位	低水位	降雨时
第一次升降	0.009	0.0068	0.67	0.11	0.465	0.068	0.0095	0.161	0.331
第二次升降	0.0097	0.0078	0.75	0.118	0.43	0.167	0.01	0.154	0.138

下载: 导出CSV

参考文献(24)

[1]	杨何, 汤明高, 蔡国军, 等. 三峡库区二道河滑坡变形机制研究[J]. 科学技术与工程,2016,16(8):66 − 71. [YANG He, TANG Minggao, CAI Guojun, et al. Research on deformation mechanism of erdaohe landslide in Three Gorges Reservoir Area[J]. Science Technology and Engineering,2016,16(8):66 − 71. (in Chinese with English abstract) DOI: 10.3969/j.issn.1671-1815.2016.08.010
[2]	汤明高, 杨何, 许强, 等. 三峡库区滑坡土体渗透特性及参数研究[J]. 工程地质学报,2019,27(2):325 − 332. [TANG Minggao, YANG He, XU Qiang, et al. Permeability and parameters of landslide bodies in Three Gorges Reservoir Area[J]. Journal of Engineering Geology,2019,27(2):325 − 332. (in Chinese with English abstract)
[3]	杨何, 汤明高, 叶润青, 等. 三峡库区滑坡堆积体非饱和土的土: 水特征研究[J]. 水利水电技术,2017,48(9):168 − 173. [YANG He, TANG Minggao, YE Runqing, et al. Study on soil-water characteristics of unsaturated soil of landslide deposits in Three Gorges Reservoir Area[J]. Water Resources and Hydropower Engineering,2017,48(9):168 − 173. (in Chinese with English abstract)
[4]	李道臣, 王志俭, 邵杰鹏, 等. 降雨及库水位耦合下白水河滑坡变形机理分析[J]. 三峡大学学报(自然科学版),2017,39(4):46 − 50. [LI Daochen, WANG Zhijian, SHAO Jiepeng, et al. Analysis on deformation mechanism of Baishui river landslide under rainfall and reservoir water level coupling[J]. Journal of China Three Gorges University (Natural Sciences),2017,39(4):46 − 50. (in Chinese with English abstract)
[5]	杨何, 曹阳健. 三峡库区白水河滑坡变形分析及评价[J]. 陕西水利,2017(2):105 − 107. [YANG He, CAO Yangjian. Deformation analysis and evaluation of Baishuihe landslide in Three Gorges Reservoir Area[J]. Shaanxi Water Resources,2017(2):105 − 107. (in Chinese with English abstract)
[6]	王力, 王世梅, 向玲. 三峡库区水位变化对树坪滑坡变形影响机制研究[J]. 长江科学院院报,2015,32(12):87 − 92. [WANG Li, WANG Shimei, XIANG Ling. Influence mechanism of deformation of Shuping landslide in Three Gorges Reservoir Area under water level variation[J]. Journal of Yangtze River Scientific Research Institute,2015,32(12):87 − 92. (in Chinese with English abstract) DOI: 10.11988/ckyyb.20140561
[7]	张永昌, 钱辈贝, 郭飞. 三峡水库水位升降作用下树坪滑坡复活机理研究[J]. 人民长江,2015,46(17):57 − 62. [ZHANG Yongchang, QIAN Beibei, GUO Fei. Study of revival mechanism of Shuping landslide under water level fluctuation of Three Gorges Reservoir[J]. Yangtze River,2015,46(17):57 − 62. (in Chinese with English abstract)
[8]	卢书强, 易庆林, 易武, 等. 三峡库区卧沙溪滑坡变形失稳机制分析[J]. 中国地质灾害与防治学报,2013,24(2):21 − 25. [LU Shuqiang, YI Qinglin, YI Wu, et al. Analysis on deformation and failure mechanism of Woshaxi landslide in the Three Gorges Reservoir Area[J]. The Chinese Journal of Geological Hazard and Control,2013,24(2):21 − 25. (in Chinese with English abstract)
[9]	殷跃平, 彭轩明. 三峡库区千将坪滑坡失稳探讨[J]. 水文地质工程地质,2007,34(3):51 − 54. [YIN Yueping, PENG Xuanming. Failure mechanism on Qianjiangping landslide in the Three Gorges Reservoir Region[J]. Hydrogeology & Engineering Geology,2007,34(3):51 − 54. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-3665.2007.03.013
[10]	熊珅, 易武, 王力, 等. 三峡库区八字门滑坡变形破坏机理分析[J]. 中国地质灾害与防治学报,2019,30(5):9 − 18. [XIONG Shen, YI Wu, WANG Li, et al. Analysis of deformation and failure mechanism of Bazimen Landslide in Three Gorges Reservoir Area[J]. The Chinese Journal of Geological Hazard and Control,2019,30(5):9 − 18. (in Chinese with English abstract)
[11]	YIN Y P, HUANG B L, WANG W P, et al. Reservoir-induced landslides and risk control in Three Gorges Project on Yangtze River, China[J]. Journal of Rock Mechanics and Geotechnical Engineering,2016,8(5):577 − 595. DOI: 10.1016/j.jrmge.2016.08.001
[12]	TANG H M, WASOWSKI J, JUANG C H. Geohazards in the three Gorges Reservoir Area, China - Lessons learned from decades of research[J]. Engineering Geology,2019,261:105267. DOI: 10.1016/j.enggeo.2019.105267
[13]	罗先启, 田斌, 彭刚. 黄腊石滑坡群石榴树包滑坡有限元分析[J]. 中国三峡建设,1998(7):15 − 17. [LUO Xianqi, TIAN Bin, PENG Gang. Analysis on Shiliushubao landslide by FEM[J]. China Three Gorges Construction,1998(7):15 − 17. (in Chinese with English abstract)
[14]	保长汉, 姜袁. 长江三峡石榴树包滑坡稳定分析[J]. 武汉水利电力大学(宜昌)学报,2000,22(2):109 − 111. [BAO Changhan, JIANG Yuan. Stability analysis of Shiliushubao landslide in Three Gorges[J]. Journal of University of Hydraulic and Electric Engineering/Yichang,2000,22(2):109 − 111. (in Chinese with English abstract)
[15]	杨学堂, 张永兴. 长江三峡黄腊石滑坡群石榴树包滑坡灾害性分析[J]. 岩石力学与工程学报,2002(5):688 − 692. [YANG Xuetang, ZHANG Yongxing. Disaster analysis on Shiliushubao landslide mass in the Huanglashi landslide group in Three Gorges of Yangtze River[J]. Chinese Journal of Rock Mechanics and Engineering,2002(5):688 − 692. (in Chinese with English abstract) DOI: 10.3321/j.issn:1000-6915.2002.05.018
[16]	杨学堂, 刘斯凤, 杨耀. 黄腊石滑坡群石榴树包滑坡涌浪数值计算[J]. 武汉水利电力大学(宜昌)学报,1998,20(3):51 − 55. [YANG Xuetang, LIU Sifeng, YANG Yao. Numerical calculation for surge of Shiliushubao landslide in Huanglashi landslide groups[J]. Journal of University of Hydraulic and Electric Engineering/Yichang,1998,20(3):51 − 55. (in Chinese with English abstract)
[17]	罗先启, 姜清辉, 葛修润, 等. 黄腊石滑坡群石榴树包滑坡稳定性的研究[J]. 岩石力学与工程学报,2001,20(1):29 − 33. [LUO Xianqi, JIANG Qinghui, GE Xiurun, et al. Study of the stability of Shiliushubao slope in huanglashi slope group[J]. Chinese Journal of Rock Mechanics and Engineering,2001,20(1):29 − 33. (in Chinese with English abstract) DOI: 10.3321/j.issn:1000-6915.2001.01.007
[18]	孟永东, 田斌, 郭其达. 三峡水库石榴树包滑坡灾害预警分析[J]. 水利水电技术,2004,35(12):23 − 27. [MENG Yongdong, TIAN Bin, GUO Qida. Hazard analyzing and predicting on Shiliushubao landslide in Three Gorges Reservoir[J]. Water Resources and Hydropower Engineering,2004,35(12):23 − 27. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-0860.2004.12.006
[19]	郑宏, 冯强, 罗先启, 等. 石榴树包滑坡机制的有限元分析[J]. 岩石力学与工程学报,2004(10):1648 − 1653. [ZHENG Hong, FENG Qiang, LUO Xianqi, et al. Finite element analysis on landslide mechanism at Shiliushubao[J]. Chinese Journal of Rock Mechanics and Engineering,2004(10):1648 − 1653. DOI: 10.3321/j.issn:1000-6915.2004.10.011
[20]	常宏, 王旭升. 滑坡稳定性变化与地下水非稳定渗流初探: 以三峡库区黄蜡石滑坡群石榴树包滑坡为例[J]. 地质科技情报,2004,23(1):94 − 98. [CHANG Hong, WANG Xusheng. Stability variation of a slope associated with transient groundwater flow∶A case study on Shiliushubao landslide in Huanglashi landslides, Three Gorges Reservoir Area, China[J]. Geological Science and Technology Information,2004,23(1):94 − 98. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-7849.2004.01.020
[21]	张立仁, 乔娟, 吕祎. 三峡库水位变化对石榴树包滑坡安全性的影响研究[J]. 三峡大学学报(自然科学版),2013,35(5):22 − 26. [ZHANG Liren, QIAO Juan, LYU Yi. Study of influence of water level change in Three Gorges Reservoir on Shiliushubao landslide safety[J]. Journal of China Three Gorges University (Natural Sciences),2013,35(5):22 − 26. (in Chinese with English abstract)
[22]	杨建英, 柯传芳, 吴润泽, 等. 库水波动与降雨作用下石榴树包滑坡稳定性分析[J]. 地质灾害与环境保护,2013,24(2):70 − 76. [YANG Jianying, KE Chuanfang, WU Runze, et al. Stability of Shiliushubao landslide with water level fluctuation of the reservoir and rainfall[J]. Journal of Geological Hazards and Environment Preservation,2013,24(2):70 − 76. (in Chinese with English abstract) DOI: 10.3969/j.issn.1006-4362.2013.02.014
[23]	李秀珍, 孔纪名, 王震宇. 石榴树包滑坡变形监测及演化趋势分析[J]. 工程地质学报,2006,14(3):320 − 326. [LI Xiuzhen, KONG Jiming, WANG Zhenyu. Deformation monitoring and development of Shiliushubao landslide on Three Gorges of Yangtze River[J]. Journal of Engineering Geology,2006,14(3):320 − 326. (in Chinese with English abstract) DOI: 10.3969/j.issn.1004-9665.2006.03.006
[24]	钟少波, 赵新建, 金璐, 等. 三峡库区石榴树包滑坡变形监测位移特征与稳定性分析[J]. 资源环境与工程,2016,30(1):76 − 79. [ZHONG Shaobo, ZHAO Xinjian, JIN Lu, et al. Analysis on displacement characteristics and stability of the deformation monitoring for the Shiliushubao landslide in the Three Gorges Reservoir Area[J]. Resources Environment & Engineering,2016,30(1):76 − 79. (in Chinese with English abstract)

施引文献

资源附件(0)

图(10) / 表(1)

计量

文章访问数: 364
HTML全文浏览量: 212
PDF下载量: 257
被引次数: 0

0. 引言
1. 基于剪切梁法的边坡响应加速度公式推导
1.1 剪切梁法的基本原理及公式推导
1.2 地震动数据处理及分类
2. 地震边坡的动力响应特征分析
2.1 输入地震动峰值加速度（PGA）
2.2 边坡材料特性
2.2.1 弹性模量
2.2.2 阻尼比
2.3 边坡几何特性
3. 拟静力法中的地震系数取值
4. 讨论
5. 结论

0. 引言
1. 基于剪切梁法的边坡响应加速度公式推导
1.1 剪切梁法的基本原理及公式推导
1.2 地震动数据处理及分类
2. 地震边坡的动力响应特征分析
2.1 输入地震动峰值加速度（PGA）
2.2 边坡材料特性
2.2.1 弹性模量
2.2.2 阻尼比
2.3 边坡几何特性
3. 拟静力法中的地震系数取值
4. 讨论
5. 结论

参考文献(24)

施引文献

资源附件(0)

三峡库区石榴树包滑坡近期变形特征与机理分析

作者简介: 杨 何(1985-)，男，四川射洪人，博士，高级工程师，主要从事地质灾害评价与预测方向的研究。E-mail：yanghexq@163.com

通讯作者: 汤明高(1978-)，男，湖北仙桃人，博士，教授，主要从事工程地质与岩土工程教学科研。E-mail：tomyr2008@163.com

计量

出版历程

Recent deformation characteristics and mechanism of the Shiliushubao landslide in the Three Gorges Reservoir Area

0. 引言

1. 基于剪切梁法的边坡响应加速度公式推导

1.1 剪切梁法的基本原理及公式推导

1.2 地震动数据处理及分类

2. 地震边坡的动力响应特征分析

2.1 输入地震动峰值加速度（PGA）

2.2 边坡材料特性

2.2.1 弹性模量

2.2.2 阻尼比

2.3 边坡几何特性

3. 拟静力法中的地震系数取值

4. 讨论

5. 结论

计量

出版历程

目录

0. 引言

1. 基于剪切梁法的边坡响应加速度公式推导

1.1 剪切梁法的基本原理及公式推导

1.2 地震动数据处理及分类

2. 地震边坡的动力响应特征分析

2.1 输入地震动峰值加速度（PGA）

2.2 边坡材料特性

2.2.1 弹性模量

2.2.2 阻尼比

2.3 边坡几何特性

3. 拟静力法中的地震系数取值

4. 讨论

5. 结论

作者简介:
杨　何(1985-)，男，四川射洪人，博士，高级工程师，主要从事地质灾害评价与预测方向的研究。E-mail：yanghexq@163.com

通讯作者:
汤明高(1978-)，男，湖北仙桃人，博士，教授，主要从事工程地质与岩土工程教学科研。E-mail：tomyr2008@163.com