Dynamic threshold analysis method of early warning and forecast based on real-time geo-hazards monitoring data
-
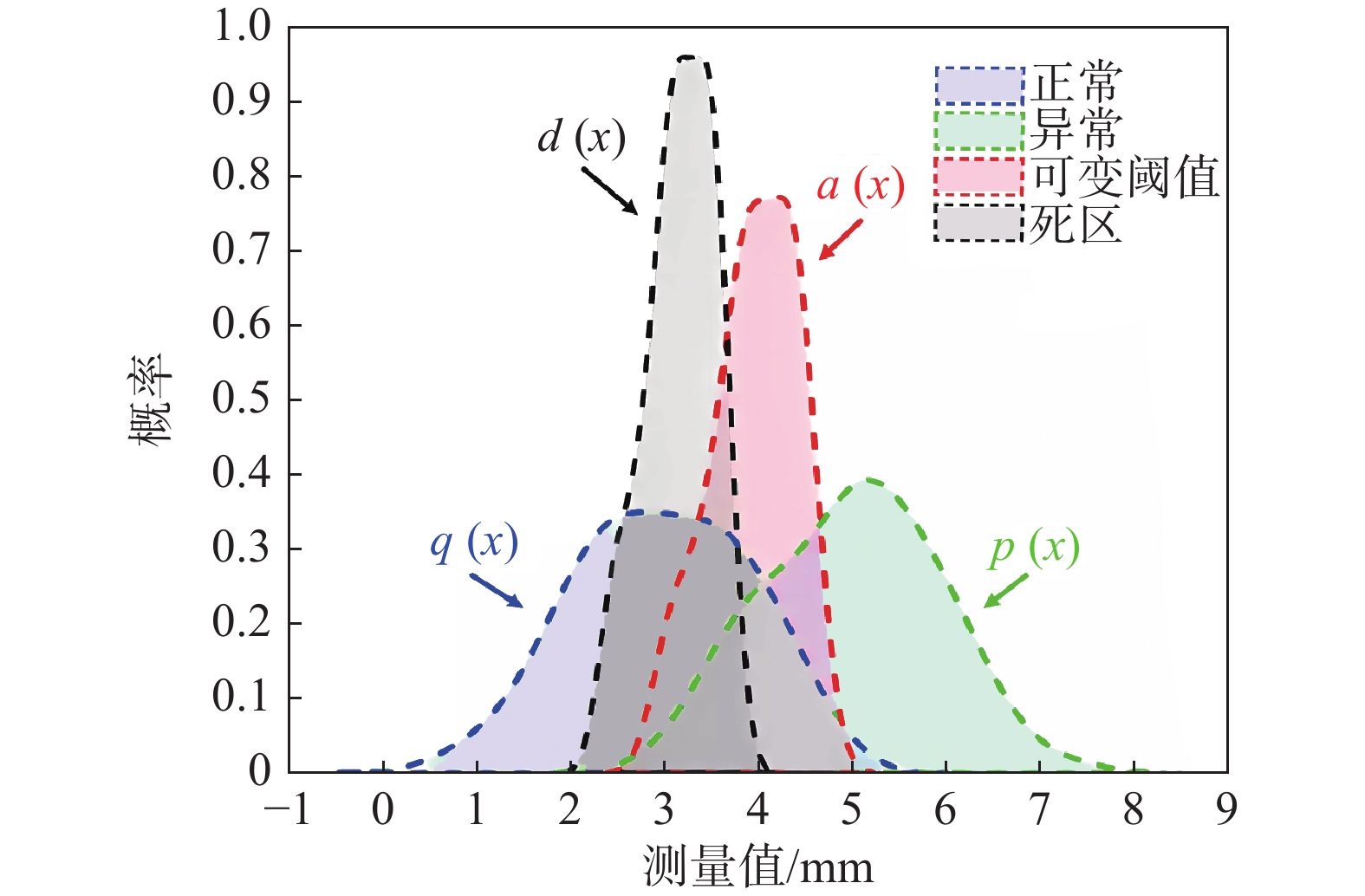
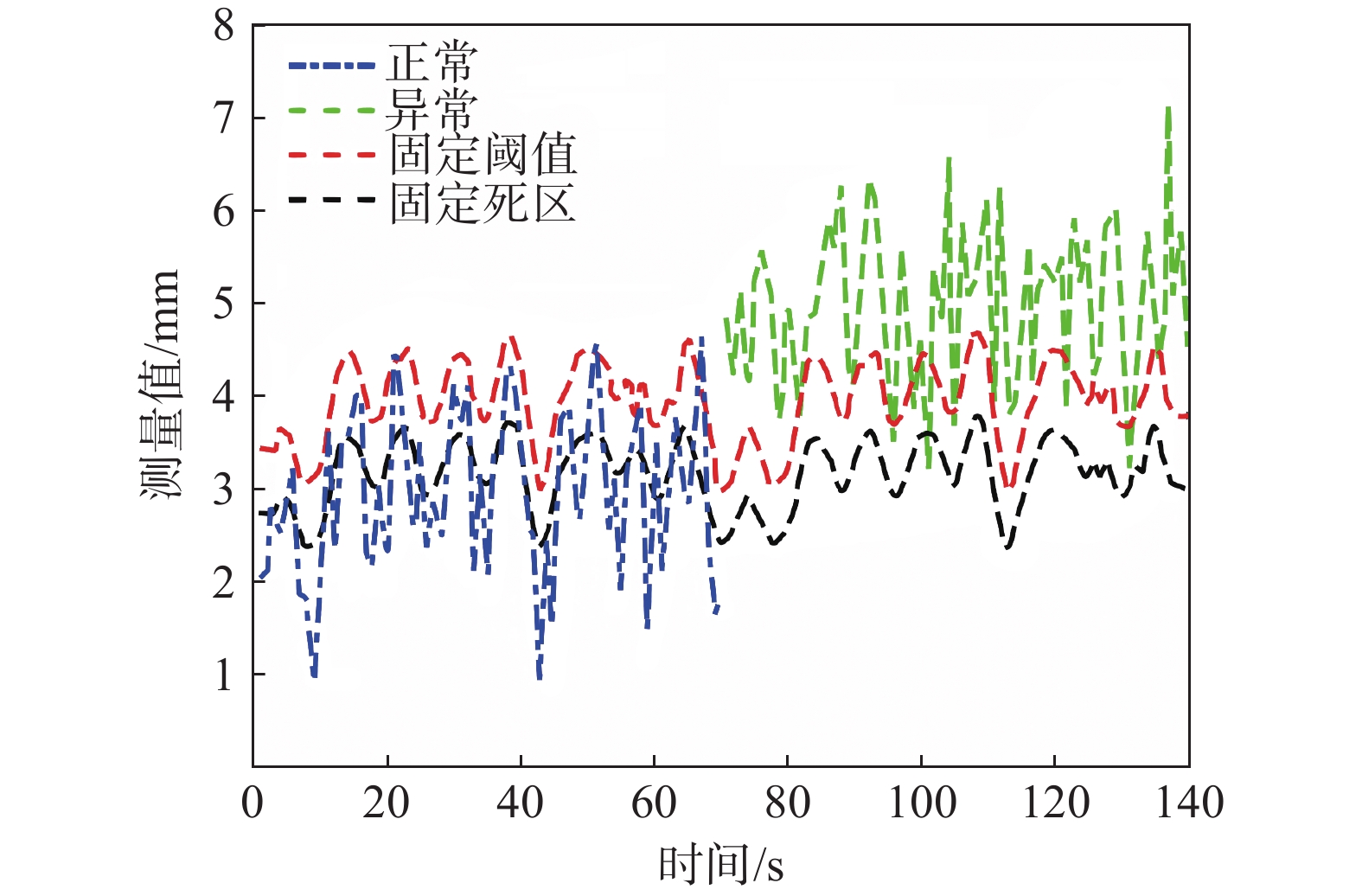
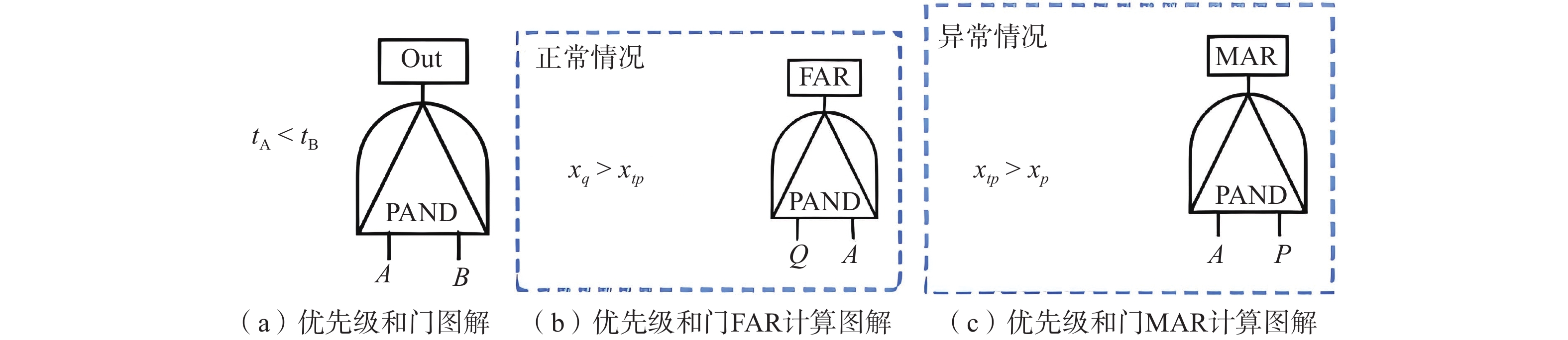
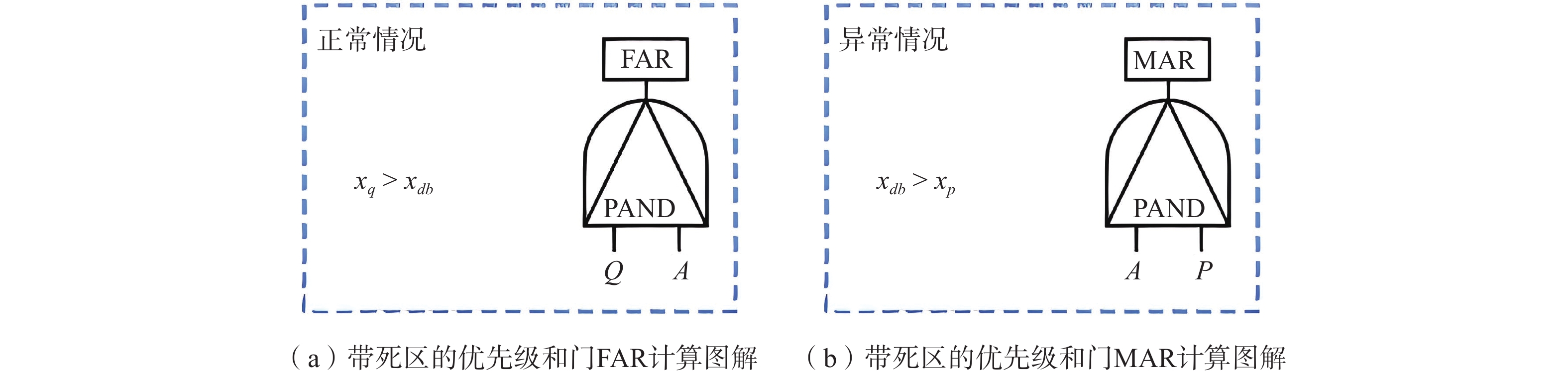
摘要: 目前在地质灾害监测领域，监测预警信息的发布主要基于各类监测设备的阈值设定。阈值是根据经验或专家估计设定，不仅对地质灾害不同类型、不同环境缺乏针对性，而且设定后较长时间不变，或根据经验略微浮动，缺少数据样本分析的科学性。另外监测设备容易受到卫星信号等环境因素影响，因此在实际运行中可能会出现误报、漏报的情况。为了解决上述问题，文中提出了一种预警阈值自学习自修正从而进行动态调整的方法，引入了两种可变阈值，并提出了一种基于优先级和门以及半马尔可夫过程 VTAS的性能指标优化新方法。半马尔可夫过程的应用使该方法能够考虑具有非高斯分布的工业测量。此外，文中还提出了一种基于遗传算法的优化设计过程，用于优化参数设置，提高性能指标。通过数值仿真以及与以往研究的比较，说明了该方法的有效性。将该方法在实测点位上进行应用，根据结果可知，相比于使用固定阈值，该方法能有效地减少系统误报、漏报，提高地质灾害预警的准确性，从而更好地保护人民生命财产安全。Abstract: Currently, in the field of geological disaster monitoring, monitoring and early warning information is mainly released based on the threshold setting of various types of monitoring equipment. However, since the thresholds are established according to empirical values or expert evaluations, there is a lack of pertinence to different types of geological disasters and different environments. Once set, these thresholds remain unchanged for a long time, and even when adjusted, they only slightly float based on experience, lacking scientific data sample analysis. Additionally, monitoring equipment is susceptible to satellite signals and environmental factors, leading to false alarms and false negatives during operation. To address these issues, a method of dynamic adjustment of self-learning and self-correction early warning thresholds is proposed. This method introduces two variable thresholds and a new performance index optimization method for VTAS based on priority and gate and semi-Markov processes. The application of the semi-Markov process allows the method to consider industrial measurements with non-Gaussian distributions. Moreover, an optimization design process based on genetic algorithms is proposed to improve performance indicators by optimizing parameter settings. Three numerical examples are used to illustrate the effectiveness of this approach and compare it with previous studies. When applied at the measured point, the method effectively reduce false alarms and under-alarms compared to the use of fixed thresholds, improving the accuracy of geological disaster early warning and better protecting the safety of people's lives and property.
-
0. 引言
地质灾害监测是地质灾害防治手段中最重要的一环，通过分析不同种类地质灾害的发育情况和影响因素，在现场有针对性的布设监测设备进行高精度实时监测。一旦灾体发生倾斜、振动等形变异常情况，监测数据达到或者超过预警阈值，那么就会触发应急预案，再对现场进行核实调查。然而，很多时候监测设备受到卫星信号等环境因素干扰时，易产生误报和漏报，浪费人力物力，造成不良影响。因此，需要不断有针对性地对设备预警阈值进行修正。
Izadi等[1]提出了一种预警阈值的方法，其基于操作特性曲线并以减少误报和持续监测为目的。其中一些学者[2-8]介绍了预警与预警阈值设计之间的关系，目的是使预警阈值能处在一个合适的区间。Sharma等[9]分析了火灾报警器的最新趋势和发展，该研究指出，大多数误报都是由于安装不良、维护不完善等人为因素造成的。研究对当前和潜在的问题和挑战提出了批判性观点。Al-Dabbagh等[10]专注于操作指标，可视化图和警报洪水作为警报系统的决策支持工具，引入了多层雷达图，以提高报警指标的可读性。Quiñones-Grueiro等[11]提出了一种基于报警-洪水临界指数的复排序设计方法数据驱动的多模过程建模与监测技术，回顾了多模式流程的建模和现有的监控方法，还研究了建模方法和监测方法的系统聚类和表征。Hollifield等[12]研究了提高报警系统性能和减少报警迫害的不同方法，在研究的滤波方法中，可以突出显示延迟定时器和死区，但是，在警报监测期间会发生一些延迟。Kondaveeti等[13]提出了另一种具有接收器工作基于特性曲线的技术，用于设计死区或阈值以降低误报率（false alarm rate，FAR）和漏报率（missing alarm rate，MAR）。Cheng等[14]引入了一种优化滤波器设计方法，以增强报警系统的性能，而不是经典的移动式滤波器。Yang等[15]使用相关色图提出了一种新的可视化方法，用于说明不同警报之间的时间滞后相关性。Han等[16]提出了一种通过优化多变量报警阈值来最小化多维空间中误报概率（FAR）和漏报概率（MAR）的方法。虽然这种方法可以减少误报的数量，但同时减少误报和漏报是不可能的。Han等[16]预发送了一种结合FAR、MAR和相关性分析的多元报警阈值优化方法，以解决报警阈值优化问题，重新对滋扰报警进行补偿。Xu等[17]引入了一种基于证据理论的在线变量阈值方法，在优化报警系统设计的同时，考虑了与过程变量相关的不确定性。Gao等[18]提出了一种基于相关性一致性的多元报警阈值优化方法。该文采用Pearson相关分析方法获得过程数据的相关系数，并采用粒子群优化（PSO）算法对问题进行优化。为了提高现有基于阈值的报警系统的效率，Bahar-Gogani等[19]利用均值变化点检测方法提出了一种扩展的自适应阈值报警系统。
尽管到目前为止已经形成了大量的研究，但据作者所知，没有一项已发表的作品通过使用优先级和门和半马尔可夫过程（SMP）的概念来考虑一种基于优先级和门以及半马尔可夫过程(variable thresholds and semi-markov processes, VTAS)的性能分析问题。本研究介绍了两种类型的VTAS（即可变阈值和带可变死区带的可变阈值），它们能够减少报警干扰并提高性能。随后，利用优先级和门的功能行为，在不同条件下对VTAS进行FAR和MAR评估，提出了一种新的方法。FAR和MAR的优先级和门模型通过创建它们的半马尔可夫模型来求解。然后通过蒙特卡罗模拟验证结果，并与其他一些现有的研究工作进行比较。为了便于报警系统的优化设计，利用遗传算法获取并分析了所提出的非高斯分布方法。这种系统化方法及其解决方案使报警系统设计人员能够更深入地了解这些系统的性能行为。
1. 问题分析
报警系统的性能主要取决于3个判断指标：FAR、MAR和平均报警延迟（AAD）。为此，将随机离散信号x(t)视为采样时间间隔为h的过程变量测量值及其相关报警触发点xtp，如图1所示。
![]()
图 1 过程变量测量值的随机离散信号x(t)Figure 1. Random discrete signal x(t) of process variable measured values根据一种广泛使用的延迟方法，如果假设数据x(t)的n个连续样本超过触发点，则会发出警报。假设正常数据是小于xtp的x(t)样本，异常数据是超过xtp的x(t)样本，如图2所示，该图可分为四个部分。
![]()
图 2 x(t)的正常、异常、假报警和错过报警部分分类Figure 2. Classification of normal, abnormal, false alarm and missed alarm parts of x(t)对正常和异常数据进行分类后，可以得到它们的概率密度函数，如图3所示。
![]()
图 3 x(t)正常部分和异常部分的分离概率密度函数Figure 3. Separation probability density function of x(t) normal part and abnormal part将测量值分为正常和异常两类后，误报和漏报概率可分别计算如下：
$$ {\rm{FAR}}={q}_{1}={\int }_{{x}_{tp}}^{+\mathrm{\infty }}q\left(x\right){\rm{d}}x $$ (1) $$ {\rm{MAR}}={p}_{2}={\int }_{-\mathrm{\infty }}^{{x}_{tp}}p\left(x\right){\rm{d}}x $$ (2) 式中：q(x)——测量正常部分的概率密度函数；
p(x)——测量异常部分的概率密度函数。
现在，假设作为测量或监控信号的x(t)在时间t0时等于或大于xtp，在ta时报警。报警延迟可定义如下：
$$ {T}_{{\rm{d}}}={t}_{a}-{t}_{0} $$ (3) 由于信号x(t)是一个离散的随机变量，因此报警延迟Td是一个随机变量。因此，平均报警延迟（AAD）定义为Td的预望值。
$$ {\overline{T}}_{{\rm{d}}}=E\left({T}_{{\rm{d}}}\right) $$ (4) 式中：E——期望函数。
一般来说，我们需要x(t0), ···, x(t0+h)的多维联合概率密度函数来计算
$ {\overline{T}}_{d} $ 。为简单起见，假设x(t)是独立的且同分布的（IID），那么Td=ih的概率密度函数可以写成：$$ P\left({T}_{{\rm{d}}}=ih\right)={p}_{2}^{i}{p}_{1} $$ (5) 式中：P——Td = ih的概率密度函数。
p1=1−p2，i=[1, 2, 3, ···]，平均报警延迟也是如此：
$$ {\overline{T}}_{{\rm{d}}}=E\left({T}_{{\rm{d}}}\right)=\sum _{i=0}^{\mathrm{\infty }}ih{p}_{2}^{i}{p}_{1}=h\frac{{p}_{2}}{{p}_{1}} $$ (6) 2. 阈值报警系统背景
本节简要介绍了有死区和无死区的简单和可变阈值报警系统。作为一种定义，当数据的绝对量大于预定阈值的量时，会出现警报，否则会清除警报。式（7）给出了考虑零平均信号数据的报警的基本定义。为了简化计算，假设系统故障以上升而非间歇故障的形式发生，我们只有一个警报生成上限（自适应限值）。然而，通过所提出的方法，可以考虑故障与回落发生及其低限值。
$$ A=\left\{\begin{split} &1 & \left|S\right|\geqslant T\\ &0 & \left|S\right|<T\end{split}\right. $$ (7) 式中：A——报警状态值；
T——阈值；
S——信号。
注意，该信号可以是基于信号的方法中的真实信号，也可以是基于模型的方法中的残余信号。
2.1 固定阈值报警系统
在这种类型的系统中，对信号应用固定阈值来诊断报警状态。可以通过以下方式实现：
$$ T=m\pm \varphi v $$ (8) 式中：m——所有数据的平均值；
$\varphi$ ——可调指数；v——标记信号中所有数据的方差值。
图4显示了信号x(t)应用的固定阈值。
表1确定了FAR和MAR这两个用于分析报警管理系统运行的指标。必须确定适当的固定阈值，以尽可能同时降低这两个指标。当固定阈值足够大时，故障灵敏度降低。相反，由于真实数据中的不确定性和干扰行为，如果静态阈值过低，错误警报的数量会增加。在这种情况下，报警信号在开启和关闭状态之间传输，称为抖动报警。
表 1 可变阈值报警系统的结果Table 1. Results of variable threshold alarm system方法 固定阈值 固定阈值和死区 可变阈值 可变阈值和死区 指标 FAR 0.2668 0.2668 0.2009 0.2009 MAR 0.2036 0.0452 0.1836 0.0448 2.2 具有死区的简单阈值报警系统
引入死区方法，在存在干扰数据的情况下提高报警管理系统的性能。事实上，死区可以被确定为清除噪声信号中警报的另一个限制。根据阈值类型（上限阈值或下限阈值），选择合适的死区。死区通常定义为阈值或变量范围的百分比。由于变量的范围通常未知，因此在这项工作中，死区表示为报警限（阈值）的一部分。
$$ dbwh=T+db $$ (9) $$ dbwh=T-db $$ (10) 式中：T——阈值；
db——死区值。
图4考虑了L=4和db=3.2。此外，表1中列出了以多种方式计算的FAR和MAR，以便进行比较。可以看出，死区限制的使用使得警报抖动比以前更好。然而，这种方法只是改进了MAR。这意味着发生的漏报更少，但这种方法不足以减少误报。
2.3 可变阈值报警系统
为了减少建模不确定性和测量噪声的影响，必须应用较大的固定阈值。然而事实上，这种解决方案可以大大减少误报。但是灵敏度也会降低。因此，这种方式是不合适的。此外，死区也不能大大减小。因此，为了使FAR最小化，引入了可变阈值。这种阈值的主要思想：干扰和其他非受控影响（如建模不确定性和测量噪声）随时间变化，阈值随时间变化。
在设计可变阈值时，定义了一个足够长的滑动窗口，并在每次滑动中计算窗口内数据的均值和方差。必须注意的是，根据信号的趋势，窗口大小可能会有所不同。此外，动量因子用于防止在可变阈值中忘记之前的数据样本。在以下等式给出了变量的计算过程。
$$ \begin{split} &\overline{v}=\gamma v\left(k-1\right)+\left(1-\gamma \right)v\left(k\right)\\ &\overline{m}=\gamma m\left(k-1\right)+\left(1-\gamma \right)m\left(k\right)\\ &T\left(k\right)=\overline{m}\left(k\right)\pm \alpha \overline{v}\left(k\right)\end{split} $$ (11) 式中：v——滑动窗口内数据的方差；
γ——动量因子；
m——滑动窗口内数据的平均值；
k——窗口序号，k=1, 2, 3, ···；
α——可调因子；
T(k)——第k个窗口中的可变阈值。
这里的主要问题是适当地选择滑动窗口长度n。如果选择的n太小，阈值会很快适应由任何因素（例如干扰、噪声或故障）引起的残差变化。如果n太大，阈值的作用方式与常数相似，决策的敏感性降低。
此外，还考虑了对信号应用可变阈值的一些假设。在本文中，假设信号的正常状态可用，并且在这种情况下可以对信号应用可变阈值。然后，将确定的可变阈值应用于实际情况下的信号进行决策。让我们考虑上述假设，k=25，γ=0.5。然后，在应用可变阈值后，异常和正常情况下的数据概率密度函数可以如图5所示。此外，表1中也列出了以这种方式计算的FAR和MAR，并将其与固定阈值进行比较。
![]()
图 5 可变阈值a(x)、死区d(x)、正常q(x)和异常p(x)信号的估计概率密度函数Figure 5. Estimated probability density function for variable thresholds, deadbands, normal and abnormal signals通过将该方法计算的FAR和MAR与前面两种方法进行比较，可以看出，与其他方法相比，该方法降低的FAR值较小。然而，与方法2（带死区的固定阈值）相比，MAR增大。为了克服这个缺点，我们引入了带可变死区的可变阈值。
2.4 具有可变死区的可变阈值报警系统
在该方法中，将可变阈值和死区进行合并，以降低FAR和MAR。如2.2节中方法所述，死区假设为报警限值的一部分。因此，由于阈值的变化，死区也应该变化。如图6所示，在信号上应用可变死区和可变阈值。与其他方法相比，该方法可以同时降低FAR和MAR。此功能是此方法相对于其他方法的优点。表1明确确认了这一问题。
3. VTAS方法
显然，在正常情况下，当第i次测量的值大于阈值（固定阈值中的xtp）时，会发出警报，称为假警报。类似地，在异常情况下，当第i个测量值小于阈值时，警报恢复正常，称为错过警报。也就是说，在正常情况下，当xq>xtp和在异常情况下发生虚警，当xtp>xP时发生漏报，其中xq表示正常情况下的测量，xp表示异常情况下的测量，xtp是阈值。为了计算FAR和MAR，需要一种系统的方法。
动态故障树是一种流行的技术，它有助于对概率和随机现象进行系统建模和说明。在动态故障树中，优先级和门用于顺序故障行为的建模。如果两个事件A和B输入至优先级和门中，则当事件A发生在事件B发生之前时，输出将为真（tA<tB）。动态故障树中的这种情况如图7（a）所示。在本文中，利用优先级和门的行为进行FAR和MAR评估。在本文的方法中，如果在x域而不是在时域中使用优先级和门，则将有一个系统的概率门，其中输入是正常测量值（q）、异常测量值（p）和可变阈值（a）的累积分布函数（cumulative distribution function，CDF）。为了实现FAR，xq>xtp是正常条件下的对象，并且可以在图7（b）中示出。同样地，为了获得MAR，xtp>xp是处于异常条件下的对象，并且可以如图7（c）所描绘。通过使用优先级和门，可以得到一种系统的FAR和MAR计算方法。如前所述，假设测量值的显著增加是异常行为的迹象。相反，如果显著下降被视为异常行为，则必须切换MAR和FAR模型中优先级和门的输入。在这种情况下，对于FAR模型，“输入A”必须分别定义为门的第一个输入，“输入Q”必须分别定义为门的第二个输入。对于MAR模型，“输入P”必须分别设置为门的第一个输入，“输入A”必须分别设置为门的第二个输入。
在相同的情况下，对于具有死区的VTAS，FAR模型可以如图8（a）所示，MAR模型可以如图8（b）所示。在这些模型中，假设警报将随上升故障而上升。因此，对于下降故障，必须按照前面的解释重建这些模型。
![]()
图 8 带死区的优先级和门计算图解Figure 8. Calculation diagrams for a priority and gate with deadband3.1 假设条件
一般来说，报警系统对环境影响、缺陷和运行模式等因素有着很大的依赖性，这使得报警系统的设计任务具有挑战性。在本文中，作出以下假设，以提高方法对实际用途的适用性。
首先将本文中的测量值假设为独立且同分布（IID）；其次所提出的方法可以对下降和上升故障类型及其相关报警进行建模，而且尖峰和短时间歇性故障将被忽略；最后假设在每个VTAS的设计过程中，正常测量和异常测量在开始时由专家进行分类。
3.2 SMP的解析解
序言中汇总并讨论了不同类型的解决方案，所有这些解决方案都可用于评估VTAS中的MAR和FAR。在本节中，将研究SMP的解析解，并结合优先级和门来计算漏报和误报的参数概率。SMP可以用不同的符号来建模。本文使用元组来进行建模，即(p, P(x), F(x))，其中：p是初始分布的向量，P(x)是条件转移概率矩阵，F(x)描述了测量值的分布函数矩阵；考虑到Xi(i = 0, 1, 2)作为一个随机变量，其次SMP由初始状态概率
$p(0)= [1,0,\cdots,0]$ ，条件转移概率矩阵$P(x)=[P_{ij}(x)] $ 的向量确定。其中，P(x)由下式计算：$$ {P}_{ij}\left(x\right)=P\left\{X\left(x\right)=j, \left(0\right)=i\right\} $$ (12) $$ {P}_{ij}\left(x\right)={\delta }_{ij}\left[1-{G}_{i}\left(x\right)\right]+\sum {\int }_{0}^{x}{P}_{ij}\left(t-x\right){\rm{d}}{Q}_{ij}\left(x\right) $$ (13) $$ {G}_{ij}\left(x\right)=P\left\{{S}_{1}\leqslant x,{X}_{0}=i\right\}=\sum _{j=1}^{i}{Q}_{ij}\left(x\right) $$ (14) $$ {Q}_{ij}\left(x\right)=P\left\{{X}_{1}=j,{S}_{1}\leqslant x,{X}_{0}=i\right\} $$ (15) 其中，Q是每个状态的分布矩阵，G为对角矩阵；如果i=j，则δij=1，否则，则δij=0；X是由x组成的向量，i, j=[0, 1, 2, ···]。S是系统在不同x下的状态。
通过应用拉普拉斯-斯蒂尔杰斯变换可以得到
$ {Q}_{ij} $ 的解。因此可以得出：$$ {c}{\tilde{p}}_{ij}(s)={\delta}_{ij}[1-{\tilde{g}}_{ij}(s)]+{\tilde {p}} _{ s}{\tilde{q}}_{ij}(s){\tilde{p}}_{ij}(s) $$ (16) 式中：c——常数；
$\tilde{g} $ ——G在时间s的值；$\tilde{q} $ 、$\tilde{p} $ ——与q、p互补。矩阵形式的等式（13）可以重写如下：
$$ \tilde{p}\left(s\right)=\left(\sum _{n=0}^{\mathrm{\infty }}\tilde{q}(s)^{n}\right)\left(I-\tilde{g}\left(s\right)\right) $$ (17) x域中的无条件状态概率矩阵确定如下：
$$ P\left(x\right)=P\left(0\right)P\left(x\right) $$ (18) 最后，通过总结某些状态的瞬态概率，可以得出FAR或MAR，这将在下一小节中进行详细讨论。
3.3 指数概率密度函数测量的FAR和MAR评估
为了简化所提方法的演示，本文考虑了异常测量和正常测量的指数概率密度函数。在优先级和门的半马尔可夫模型中，FA(x)是优先级和门的第二个输入的累积分布函数（可变阈值的累积分布函数），FQ(x)是优先级和门的第一个输入的累积分布函数。分别以从上到下和从左到右进行编号。该模型可通过上一小节中描述的SMP定理求解。核矩阵可以写成如式（18）的形式，每个状态的分布矩阵是式（19）的形式。
$$ Q\left(x\right)=\left[\begin{array}{ccccc}0& {Q}_{\mathrm{1,2}}& {Q}_{\mathrm{1,4}}& 0& 0\\ 0& 0& 0& {Q}_{\mathrm{2,3}}& 0\\ 0& 0& 0& 0& {Q}_{\mathrm{4,5}}\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right] $$ (19) $$ \begin{split}{\boldsymbol{G}}\left(x\right)=&{\rm{diag}}(1-(1-{F}_{A}\left(x\right))(1-{F}_{Q}(x)),{F}_{A}(x)\\ &{F}_{Q}(x),\delta (x-\infty ),\delta (x-\infty ))\end{split} $$ (20) 式中：diag——创建对角矩阵的函数；
$\delta $ ——狄拉克函数。$$ \begin{split} {Q}_{\mathrm{1,2}}& ={\int }_{0}^{x}\left[1-\left(1-{e}^{-{\lambda }_{A}\tau }\right)\right]{\rm{d}}\left\{1-{e}^{-{\lambda }_{Q}\tau }\right\}\\ & ={\int }_{0}^{x}{e}^{-\left({\lambda }_{A}+{\lambda }_{Q}\right)\tau }{\lambda }_{Q}{\rm{d}}\tau =\frac{{\lambda }_{Q}\left[1-{e}^{-\left({\lambda }_{A}+{\lambda }_{Q}\right)x}\right]}{{\lambda }_{A}+{\lambda }_{Q}}\end{split} $$ (21) $$ \begin{split}{Q}_{\mathrm{1,4}}& ={\int }_{0}^{x}\left[1-\left(1-{e}^{-{\lambda }_{Q}\tau }\right)\right]{\rm{d}}\left\{1-{e}^{-{\lambda }_{A}\tau }\right\}\\ & ={\int }_{0}^{x}{e}^{-\left({\lambda }_{A}+{\lambda }_{Q}\right)\tau }{\lambda }_{A}{\rm{d}}\tau =\frac{{\lambda }_{A}\left[1-{e}^{-\left({\lambda }_{A}+{\lambda }_{Q}\right)x}\right]}{{\lambda }_{A}+{\lambda }_{Q}}\end{split} $$ (22) $$ {Q}_{\mathrm{2,3}}={\int }_{0}^{x}{\lambda }_{A}{e}^{-{\lambda }_{A}\tau }{\rm{d}}\tau =1-{e}^{-{\lambda }_{A}x} $$ (23) $$ {Q}_{\mathrm{4,5}}={\int }_{0}^{x}{\lambda }_{Q}{e}^{-{\lambda }_{Q}\tau }{\rm{d}}\tau =1-{e}^{-{\lambda }_{Q}x} $$ (24) 式中：λ——门的输入系数；
τ——输出系数。
可使用式（23）从失效状态的概率获得优先级和门输出的概率。
$$ {\rm{FAR}}={{q}}\left(x\right)={T}^{-1}\left\{{q}_{\mathrm{1,4}}\left(s\right)\left({f}_{Q}^{*}\left(s\right)\right)\right\} $$ (25) 同样，MAR的概率将得到：
$$ {\rm{MAR}}={{P}}\left(x\right)={T}^{-1}\left\{{q}_{\mathrm{1,4}}\left(s\right)\left({f}_{P}^{*}\left(s\right)\right)\right\} $$ (26) 式中：T——阈值；
s——时间/s；
${f}_{Q}^{*} $ ——0到$+\infty $ 的积分；${f}_{P}^{*} $ ——0到$-\infty $ 的积分。3.4 蒙特卡罗模拟验证
通过一千万次重复的蒙特卡罗模拟验证了所提出的半马尔可夫方法，并且在每次迭代中，生成的混淆矩阵的假正值和负值都存储在向量中。仿真完成后，将假阳性和假阴性的均值和方差值分别计算为FAR和MAR。表2提供了VTAS解决方案和蒙特卡罗模拟之间的比较。根据表2，验证了VTAS方法的正确性。
表 2 蒙特卡罗模拟与VTAS方法的比较Table 2. Comparison between Monte Carlo simulation and VTAS方法 蒙特卡罗模拟 VTAS的解 指标 FAR 0.159852 0.15867 MAR 0.159856 0.15867 3.5 遗传算法优化
在设计最优报警系统时，可以考虑多目标进化算法。遗传算法是求解优化问题的著名元启发式算法之一。遗传算法的第一步是生成随机解的初始总体。下一个步骤是选择操作，其中使用选择函数从当前总体中选择两个或多个解决方案。然后，对这些解执行交叉操作以生成新解。然后以给定的变异概率对新解进行变异。
在这种方法中，输入变量（正常和异常测量中的样本警报数（n, m）、样本窗口宽度（ω）和VTAS中的α被假定为基因型，表型将是FAR、MAR和平均警报检测。输入的分布服从一致函数，其中n和m的低值为1，高值为20。α参数的范围为20到30。此外，窗户的长度在20到100之间。选择每代成本最低的顶级基因作为交叉函数的输入，生成下一个群体。同时，突变函数生成新的随机基因并将其添加到下一个群体中。此过程将重复一定次数的迭代，以达到最佳值（最低成本）。
在优化过程中，每代考虑40个种群；突变率为35%，单点交叉率为50%，重组率为15%。报警系统设计、报警延迟和AAD取决于一些报警样本（n−m） 增加n或m会导致AAD值增加。此外，无论α和w对MAR和FAR的影响如何，在大多数情况下，增加报警样本数n，m会导致MAR和FAR值降低。为了在AAD、MAR和FAR的优化之间进行权衡，加权和成本函数可用作
$ J\left(\alpha ,w,n,m\right) $ 。$$ J\left(\alpha ,w,n,m\right)={\omega }_{1}\frac{\rm{FAR}}{I_{\rm{RFAR}}}+{\omega }_{2}\frac{\rm{MAR}}{I_{\rm{RMAR}}}+{\omega }_{3}\frac{\rm{AAD}}{I_{\rm{RAAD}}} $$ (27) 式中：IRFAR、IRMAR和IRAAD——FAR、MAR和AAD的 补数；
${\omega }_{1} $ 、${\omega }_{2} $ 、${\omega }_{3} $ ——权重系数。注意，由于nm样本报警延迟的不同延迟，AAD被分为两部分，分别用于n和m样本的延迟。根据实际情况，每个FAR、MAR和AAD的重要性可分别通过ω1、ω2、ω3进行加权。引入的权重可以根据应用程序进行不同的选择。例如，如果在假设的系统中，延迟减少是最重要的问题，且MAR优先于FAR，则成本函数J(α, w, m, n)的权重应视ω1<ω2<ω3。作为遗传算法（genetic algorithm，GA）优化的结果，可以实现“报警样本数（n，m）”、“自适应阈值的α系数”和“自适应阈值的窗口大小w”的最佳值。换句话说，优化问题的目标可以写为：
$$ \left(\alpha ,w,n,m\right)=\mathrm{arg}\min J\left(\alpha ,w,n,m\right) $$ (28) 下面，通过一些案例研究，说明了所提出的方法和GA优化的有效性。
4. 仿真
在本节中，提供了2个实例来说明基于半马尔可夫解的能力，并将所提出方法的有效性与其他已发表的研究进行比较。
4.1 实例1：威布尔分布测量
在前面的章节中，我们研究了一个具有分段白高斯随机分布的测量示例，并给出了这个示例来说明所提出的方法在非高斯随机分布中的有效性。因此，威布尔分布采用以下表达式考虑。假设生成的数据长度为200，其中0到100的测量值服从Fnormal，101到200的测量值遵循Fabnormal。
$$ {F}_{\text{normal}}\left(x\right)=1-{e}^{-{\left(\tfrac{x}{A}\right)}^{B}},A=1,B=1.3 $$ (29) $$ {F}_{\text{abnormal}}\left(x\right)=1-{e}^{-{\left(\tfrac{x}{A}\right)}^{B}},A=5,B=2 $$ (30) 式中：Fnormal——正常的概率密度；
Fabnormal——异常的概率密度。
正常和异常假设测量的概率密度函数曲线如图9所示。表3分别显示了通过蒙特卡罗模拟、拟议方法和简单马尔可夫解计算的FAR和MAR。从表3中可以看出，所提出的方法和蒙特卡罗模拟的结果是相同的。然而，有两种方法可以使用简单的马尔可夫解：①计算正常和异常测量的平均值和方差，并使用分析正态分布表达式；②使用数值概率密度函数估计。由于测量值的非高斯行为，本例中基于马尔可夫的简单解的结果是不精确的。
![]()
图 9 测量的概率密度函数（威布尔分布）Figure 9. Probability density function (Weibull distribution) of measurements表 3 所提出的解、蒙特卡罗结果和简单马尔可夫解之间的比较Table 3. Comparison between the proposed solution, Monte Carlo results and simple Markov solutions方法 VTAS的解 蒙特卡罗结果 简单马尔可夫解 指标 FAR 0.1371 0.1371 0.1455 MAR 0.1371 0.1070 4.2 实例2：高斯分布的测量
假设生成的测量值x(t)为“分段白高斯随机变量”，不精确的平均值和方差为下列公式。随机数生成的采样率为1 s，x(t)如图10所示。
$$ \left\{\begin{split} &x(t)=N\left(\mu_{1}, \sigma_{1}^{2}\right) \left\{\begin{array}{l} \mu_{1}=U(0.2 ,0 .3) \\ \sigma_{1}=U(1.5,1.6) \end{array}, \; t < 2\;000\right. \\ &x(t)=N\left(\mu_{2}, \sigma_{2}^{2}\right) \left\{\begin{array}{l} \mu_{2}=U(1.2,1.5) \\ \sigma_{2}=U(1.5,1.6) \end{array},\; t\geqslant 2\;000\right. \end{split}\right. $$ (31) 式中：U——均匀分布的随机变量；
t——时间/s；
μ——期望值；
$\sigma $ ——方差；N——正态分布。
在本例中，假设测量的静态分布部分已知，且不精确，因为x(t)混合了认知和假设不确定性。如图10所示，这是简单阈值决策的挑战性示例。然而，通过使用一个采样延迟和权重系数为0.05的指数加权移动平均（EWMA）滤波器，可以从图10中获得图11。很明显，EWMA过滤器的使用简化了决策过程，并改善了MAR和FAR。
![]()
图 11 使用具有自适应阈值的EWMA过滤器（alpha=0.5，窗口大小=100）后生成的随机数Figure 11. Generated random numbers after filtering with an EWMA filter （alpha=0.5, window size =100） with adaptive threshold表4提供了可变阈值与其他现有方法之间性能指标（MAR和FAR）的比较结果，如固定阈值（ST）和指数加权移动平均EWMA报警系统、循证报警系统evidence-based alarm system和三阶移动平均滤波器（3OMAF）、三样本报警延迟计时器（3SADT）。根据这些结果，使用EWMA滤波器的VTAS比其他方法具有更好的性能指标。
表 4 可变阈值与其他方法性能指标的比较结果Table 4. Comparison results of performance metrics of variable threshold method with other methods方法 ST VTAS EWMA VTAS
（+EWMA filter）Evidence-based alarm
system3OMAF 3SADT 指标 MAR 0.3519 0.3118 0.0437 0.0518 0.0582 0.2470 0.1511 FAR 0.3806 0.2860 0.0447 0.0241 0.0429 0.2926 0.2527 5. 应用
将上述方法应用于地质灾害监测预警系统中某实时监测点位上进行实测。
图12展示出了传感器的输出信号，其中曲线的绿色表示异常状态，蓝色表示正常状态。在图12中，设计的自适应阈值用红色表示。假设系统中不存在持续时间很短的间歇性故障。因此，正常信号（蓝色）中观察到的峰值不被视为异常事件或情况。它们可能是间歇性故障、高振幅噪音或干扰。然而，即使这些峰值是异常的，根据我们的假设，我们也必须忽略它们。
![]()
图 12 用自适应阈值（α=20）测量传感器（时间（s）-振动测量x(t) mm/s）Figure 12. Measuring sensors with adaptive threshold (α = 20)在图13中，正常/异常条件下测量的概率密度函数和设计的自适应阈值分别用绿色、蓝色和红色表示。此图显示了可变阈值的估计概率密度函数遵循与正常数据的概率密度函数类似的模式，正如所预期的那样。
![]()
图 13 传感器在正常和异常情况下的概率密度函数（测量范围-概率）Figure 13. Probability density function of sensor under normal and abnormal conditions表5描述了几种报警系统性能评估的比较结果。可以看出，通过使用带死区的固定阈值，FAR增加MAR降低。此外，在可变阈值带死区系统中，FAR增加。然而，可变阈值带死区系统可以比其他系统更好地降低MAR。根据GA优化部分，不同的需求导致不同的优化结果。根据优先级和确定的成本函数系数，将获得VTAS的不同值。如表6所示，当允许使用样本延迟时，AAD的值将增加，MAR和FAR将按预期降低。
表 5 不同方法性能指标的比较结果Table 5. Comparison results of different methods’performance metrics方法 固定阈值 可变阈值（带死区） 固定阈值（带死区） 指标 FAR 0.192783 0.289527 0.228910 MAR 0.460713 0.207569 0.364654 表 6 用遗传算法优化VTASTable 6. Optimizing VTAS with genetic algorithm遗传算法中损失函数的权重 报警系统参数
（α, ω, n, m）MAR FAR AAD ω3 ω2 ω1 （25.024, 82, 1, 1） 0.2109 0.2282 1.2674 1 1 10 IRAAD IRFAR IRMAR 1 1e−05 1e−05 ω3 ω2 ω1 （25.039, 82, 2, 3） 0.0556 0.1681 2.8742 100 0.1 0.1 IRAAD IRFAR IRMAR 1 1e−03 1e−03 ω3 ω2 ω1 （25.680, 83, 2, 3） 0.0596 0.1625 2.8979 100 0.5 0.1 IRAAD IRFAR IRMAR 1 1e−03 1e−03 首先选择传统的固定阈值方法计算得到固定的预警阈值，其结果如图14所示，由于系统数据跳变触发阈值，产生很多的误报警，使得报警数量增多。而采用本文的动态阈值估算方法，通过选择180 d时间序列的监测值,确定滑动窗口的长度为200，如图15所示。通过阈值的不断调整，得到如图16所示的结果。并结合表7和表8可以看出，采用预警数量得到了进一步的减少，并且预警性能指标得到明显改善。
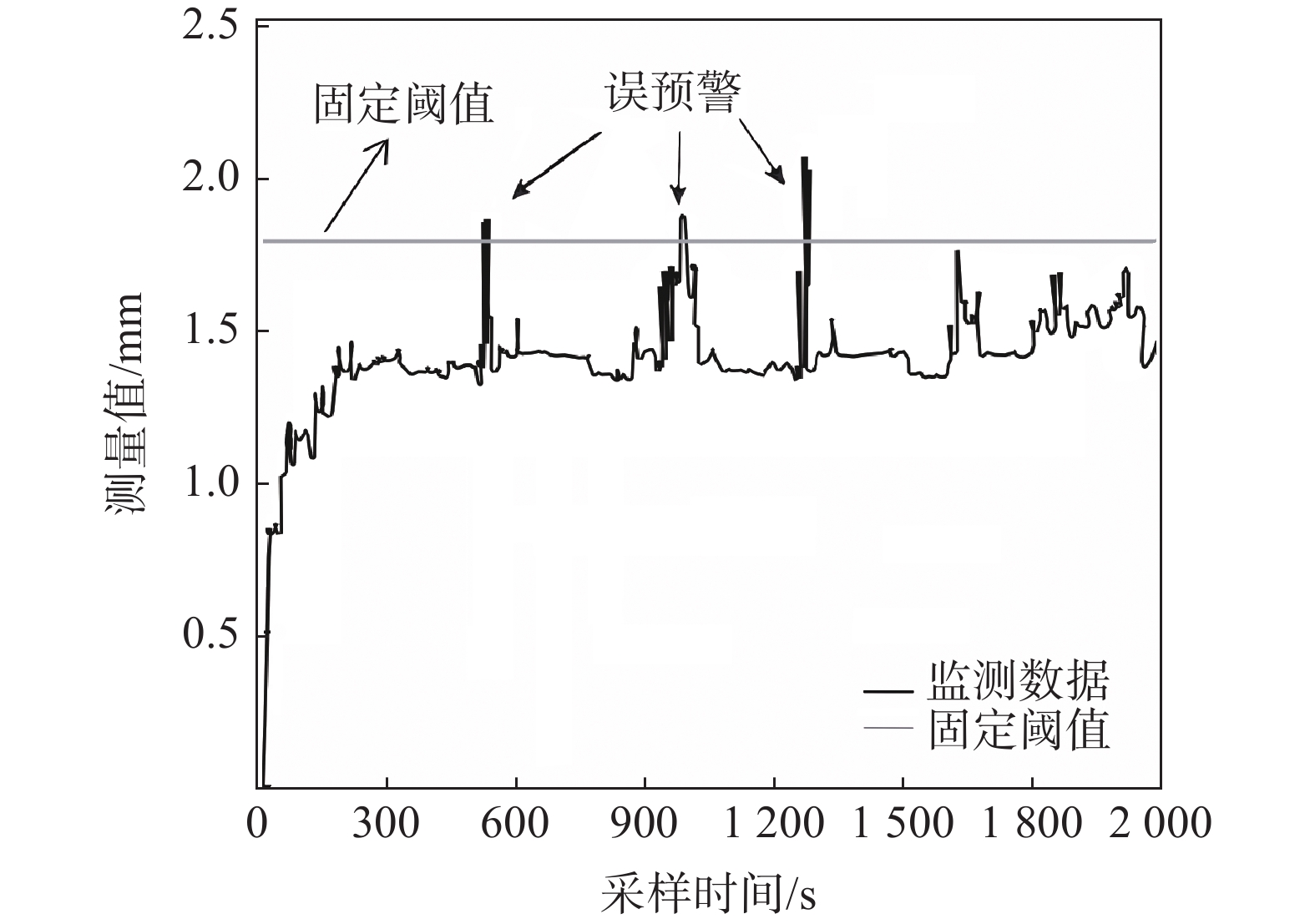
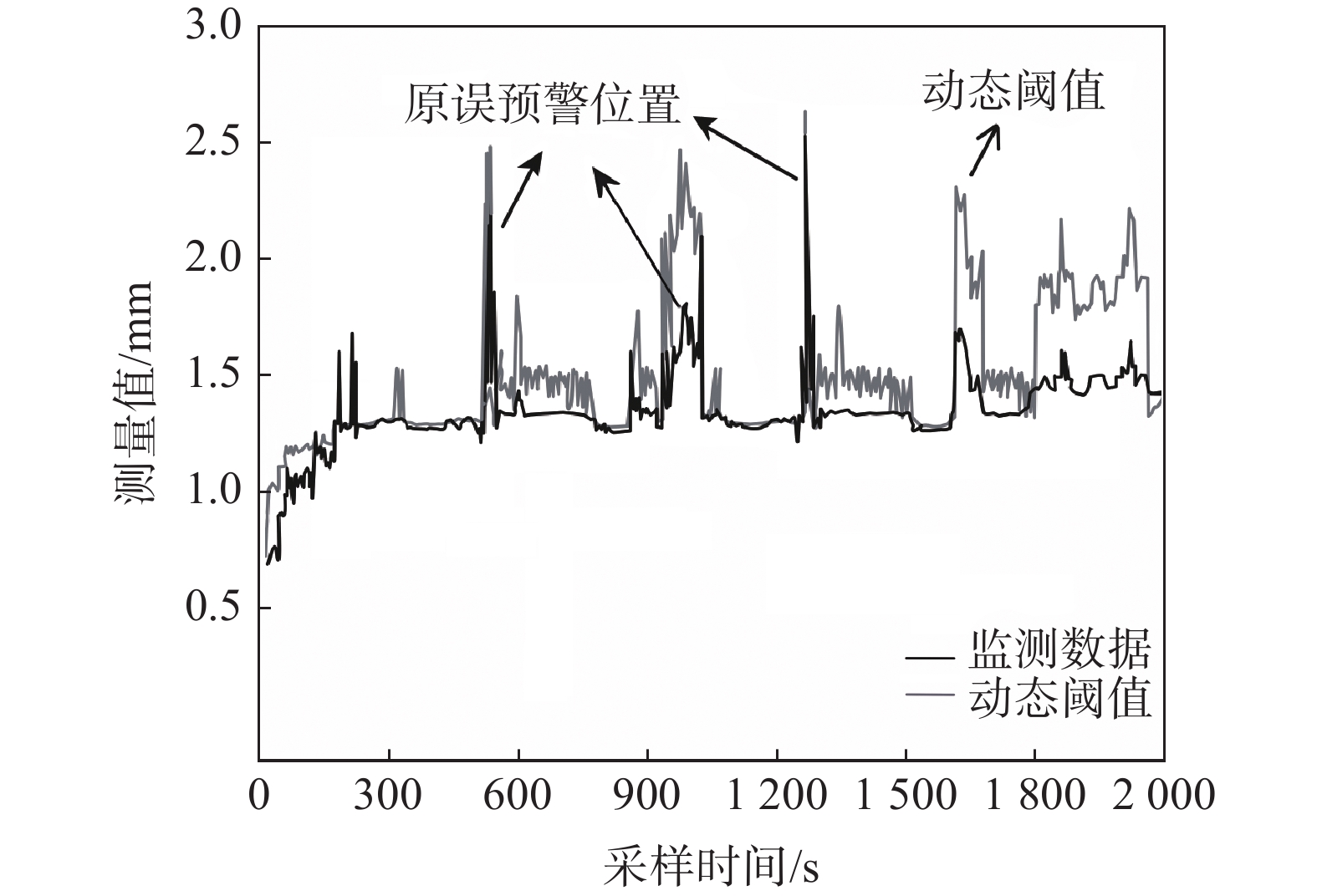
表 7 预警次数对比Table 7. Comparison of warning times方法 预警次数 固定阈值 301 可变阈值（带死区） 62 表 8 预警性能指标对比Table 8. Comparison of early warning performance indicators方法 MAR FAR 固定阈值 0.0830 0.137 可变阈值（带死区） 0.0007 0.013 6. 结论
可变阈值报警系统广泛应用于许多行业，以减少报警干扰。在本研究中，首先介绍了报警系统的主要性能指标FAR和MAR。随后，将优先级和门概念用于MAR和FAR的建模。针对MAR和FAR模型的评估，提出了基于SMP的解析解，该解可扩展到有无可变死区的不同类型VTAS，并利用半马尔可夫过程对具有非高斯特性的报警系统进行了性能优化。此外，本研究将所提出的VTAS方法与遗传算法相结合，以获得最佳的参数选择。
本文通过仿真与相关研究工作进行比较，结果表明使用EWMA滤波器的VTAS比其他方法具有更好的性能指标，证明了该方法的有效性。基于此，本文还将提出的方法应用于实际案例中，结果表明，当使用固定阈值时，FAR为0.19，MAR为0.46，当应用本文提出的方法得到可变阈值后，FAR降低到0.29，MAR降低为0.21。 以上结果表明，相比于使用固定阈值，可变阈值系统能有效地减少误报及漏报，增加预警的准确性，全面提升相关单位对突发性地质灾害的分析、预警、处置和服务的能力，为政府相关部门进行地质环境与地质灾害决策管理和社会服务提供技术保障。
-
![]()
图 1 过程变量测量值的随机离散信号x(t)
Figure 1. Random discrete signal x(t) of process variable measured values
![]()
图 2 x(t)的正常、异常、假报警和错过报警部分分类
Figure 2. Classification of normal, abnormal, false alarm and missed alarm parts of x(t)
![]()
图 3 x(t)正常部分和异常部分的分离概率密度函数
Figure 3. Separation probability density function of x(t) normal part and abnormal part
![]()
图 5 可变阈值a(x)、死区d(x)、正常q(x)和异常p(x)信号的估计概率密度函数
Figure 5. Estimated probability density function for variable thresholds, deadbands, normal and abnormal signals
![]()
图 8 带死区的优先级和门计算图解
Figure 8. Calculation diagrams for a priority and gate with deadband
![]()
图 9 测量的概率密度函数（威布尔分布）
Figure 9. Probability density function (Weibull distribution) of measurements
![]()
图 11 使用具有自适应阈值的EWMA过滤器（alpha=0.5，窗口大小=100）后生成的随机数
Figure 11. Generated random numbers after filtering with an EWMA filter （alpha=0.5, window size =100） with adaptive threshold
![]()
图 12 用自适应阈值（α=20）测量传感器（时间（s）-振动测量x(t) mm/s）
Figure 12. Measuring sensors with adaptive threshold (α = 20)
![]()
图 13 传感器在正常和异常情况下的概率密度函数（测量范围-概率）
Figure 13. Probability density function of sensor under normal and abnormal conditions
表 1 可变阈值报警系统的结果
Table 1 Results of variable threshold alarm system
方法 固定阈值 固定阈值和死区 可变阈值 可变阈值和死区 指标 FAR 0.2668 0.2668 0.2009 0.2009 MAR 0.2036 0.0452 0.1836 0.0448 
下载: 导出CSV
表 2 蒙特卡罗模拟与VTAS方法的比较
Table 2 Comparison between Monte Carlo simulation and VTAS
方法 蒙特卡罗模拟 VTAS的解 指标 FAR 0.159852 0.15867 MAR 0.159856 0.15867
下载: 导出CSV
表 3 所提出的解、蒙特卡罗结果和简单马尔可夫解之间的比较
Table 3 Comparison between the proposed solution, Monte Carlo results and simple Markov solutions
方法 VTAS的解 蒙特卡罗结果 简单马尔可夫解 指标 FAR 0.1371 0.1371 0.1455 MAR 0.1371 0.1070
下载: 导出CSV
表 4 可变阈值与其他方法性能指标的比较结果
Table 4 Comparison results of performance metrics of variable threshold method with other methods
方法 ST VTAS EWMA VTAS
（+EWMA filter）Evidence-based alarm
system3OMAF 3SADT 指标 MAR 0.3519 0.3118 0.0437 0.0518 0.0582 0.2470 0.1511 FAR 0.3806 0.2860 0.0447 0.0241 0.0429 0.2926 0.2527
下载: 导出CSV
表 5 不同方法性能指标的比较结果
Table 5 Comparison results of different methods’performance metrics
方法 固定阈值 可变阈值（带死区） 固定阈值（带死区） 指标 FAR 0.192783 0.289527 0.228910 MAR 0.460713 0.207569 0.364654
下载: 导出CSV
表 6 用遗传算法优化VTAS
Table 6 Optimizing VTAS with genetic algorithm
遗传算法中损失函数的权重 报警系统参数
（α, ω, n, m）MAR FAR AAD ω3 ω2 ω1 （25.024, 82, 1, 1） 0.2109 0.2282 1.2674 1 1 10 IRAAD IRFAR IRMAR 1 1e−05 1e−05 ω3 ω2 ω1 （25.039, 82, 2, 3） 0.0556 0.1681 2.8742 100 0.1 0.1 IRAAD IRFAR IRMAR 1 1e−03 1e−03 ω3 ω2 ω1 （25.680, 83, 2, 3） 0.0596 0.1625 2.8979 100 0.5 0.1 IRAAD IRFAR IRMAR 1 1e−03 1e−03
下载: 导出CSV
表 8 预警性能指标对比
Table 8 Comparison of early warning performance indicators
方法 MAR FAR 固定阈值 0.0830 0.137 可变阈值（带死区） 0.0007 0.013
下载: 导出CSV
-
[1] IZADI S L, SHAH D S, SHOOK S R, et al. A framework for optimal design of alarm systems[C]//Proceedings of the 7th IFAC SAFEPROCESS, 2009.
[2] NAGHOOSI E, IZADI I, CHEN T W. A study on the relation between alarm deadbands and optimal alarm limits[C]//Proceedings of the 2011 American Control Conference. June 29 - July 1, 2011, San Francisco, CA, USA. IEEE, 2011: 3627 − 3632.
[3] XU J. Performance assessment and design for univariate alarm systems based on FAR,MAR,and AAD[J]. IEEE Transactions on Automation Science and Engineering,2012,9(2):296 − 307. DOI: 10.1109/TASE.2011.2176490
[4] NAGHOOSI E,IZADI I,CHEN T. Estimation of alarm chattering[J]. Journal of Process Control,2011,21(9):1243 − 1249. DOI: 10.1016/j.jprocont.2011.07.015
[5] YUE C, IZADI I. Tongwen optimal alarm signal processing: Filter design and performance analysis[J]. J. Automation Science and Engineering, 2013, 10（2）: 446 − 451.
[6] ADNAN N A,CHENG Y,IZADI I,et al. Study of generalized delay-timers in alarm configuration[J]. Journal of Process Control,2013,23(3):382 − 395. DOI: 10.1016/j.jprocont.2012.12.013
[7] ADNAN N A,IZADI I,CHEN T W. On expected detection delays for alarm systems with deadbands and delay-timers[J]. Journal of Process Control,2011,21(9):1318 − 1331. DOI: 10.1016/j.jprocont.2011.06.019
[8] YANG Fan, SHAH Sirish L, XIAO Deyun. Correlation analysis of alarm data and alarm limit design for industrial processes[C]//Proceedings of the 2010 American Control Conference. June 30 - July 2, 2010, Baltimore, MD, USA. IEEE, 2010: 5850 − 5855.
[9] SHARMA V, et al. A critical review on the application and problems caused by false alarms[J]. Singapore, 2018, s. n.
[10] AL-DABBAGH A W,HU Wenkai,LAI Shiqi,et al. Toward the advancement of decision support tools for industrial facilities:Addressing operation metrics,visualization plots,and alarm floods[J]. IEEE Transactions on Automation Science and Engineering,2018,15:1883 − 1896. DOI: 10.1109/TASE.2018.2827309
[11] QUIÑONES-GRUEIRO M, PRIETO-MORENO A, VERDE C, et al. Data-driven monitoring of multimode continuous processes: A review[J]. Chemometr Intell Lab Syst 2019, 189（1）: 56 – 71.
[12] HOLLIFIELD BR, HABIBI E, PINTO J. Alarm management: A comprehensive guide[J]. International Society of Automation （ISA）, 2021, s. l.
[13] KONDAVEETI S R,SHAH S L,IZADI I. Application of multivariate statistics for efficient alarm generation[J]. IFAC Proceedings Volumes,2009,42(8):657 − 662. DOI: 10.3182/20090630-4-ES-2003.00109
[14] CHENG Y,IZADI I,CHEN T W. Optimal alarm signal processing:filter design and performance analysis[J]. IEEE Transactions on Automation Science and Engineering,2013,10(2):446 − 451. DOI: 10.1109/TASE.2012.2233472
[15] YANG H,LI H G. Optimization of process alarm thresholds:A multidimensional kernel density estimation approach[J]. Process Safety Progress,2014,33(3):292 − 298. DOI: 10.1002/prs.11658
[16] HAN Liu,GAO Huihui,XU Yuan,et al. Combining FAP,MAP and correlation analysis for multivariate alarm thresholds optimization in industrial process[J]. Journal of Loss Prevention in the Process Industries,2016,40:471 − 478. DOI: 10.1016/j.jlp.2016.01.022
[17] XU Xiaobin, LI Shibao, SONG Xiaojing, et al. The optimal design of industrial alarm systems based on evidence theory[J]. Control Eng Pract 2019, 46（1）: 142 – 56.
[18] GAO Huihui, LIU Feifei, ZHU Qunxiong. A correlation consistency based multivariate alarm thresholds optimization approach[J]. ISA Transactions, Volume 65, 2016: 37 − 43.
[19] BAHAR-GOGANI M, ASLANSEFAT K, SHOOREHDELI M A. A novel extended adaptive thresholding for industrial alarm systems[C]//2017 Iranian Conference on Electrical Engineering （ICEE）. May 2-4, 2017. Tehran, Iran. IEEE, 2017.
-
期刊类型引用(3)
1. 丁文海，王朋伟，安玉科，宋金光. 基于监测数据的抗滑桩变形机理与预警判据研究. 公路. 2024(08): 152-159 . 
百度学术
2. 张文政，邢真强. 煤矿热动力灾害智能预警软件开发及系统集成. 山东煤炭科技. 2024(11): 74-78 . 百度学术
3. 肖自为，马源，李金林，龚弦，邓修林，程曦. 基于过程预警模型的矿山边坡监测系统研究与应用. 地质灾害与环境保护. 2024(04): 91-98 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 1507
- HTML全文浏览量: 991
- PDF下载量: 294
- 被引次数: 3
邮件订阅
RSS