Dynamic fragmentation characteristics of rock avalanche with tectonic joints
-
摘要:
近年来西南地区崩塌灾害频发,严重影响区域生态环境和人类活动。为明确崩塌体运动过程中的破碎特征,基于对贵州毕节纳雍县鬃岭崩塌的野外地质勘察,使用离散元颗粒流方法模拟了鬃岭崩塌在破坏及堆积阶段的动力破碎过程,并对崩塌体中破碎体的最大弗雷特直径(feret’s diameter)分布特征进行统计分析。结果表明:(1)重力作用下鬃岭崩塌内部构造节理迅速贯通,将崩塌体分割为大量破碎块体,最终沿顺倾节理面滑下。(2) 在崩塌前期破坏及后续堆积过程中均存在明显的破碎现象,具体表现为初始破坏时的大范围解体与后续堆积过程中的摩擦拉裂破碎。(3)采用双参数Weibull分布模型及分形几何理论拟合了不同时刻破碎体粒径分布曲线,结果显示崩塌体在堆积阶段(t = 21.7~72.4 s)的破碎程度弱于前期破坏阶段(t = 0~21.7 s)的破碎程度,破碎体的分形维数及细粒径破碎体的占比在整个运动过程中不断增大,再次论证了崩塌体破坏及堆积全过程中的破碎解体现象。研究结果为揭示鬃岭崩塌的动力破碎机理提供了理论依据,为西南山区崩塌灾害的防治提供了科学指导。
Abstract:In recent years, rock avalanche disasters have been occurring frequently in southwest China, which seriously affect the regional ecological environment and human activities. To understand the fragmentation characteristics of the avalanche masses during their movement, this study is based on the field investigation of the rock avalanche in Zongling Town, Nayong County. The dynamic fragmentation process of the rock avalanche during the failure and accumulation stages was simulated using the particle discrete element method. Additionally, the distribution characteristics of the maximum feret’s diameter of the fragments within the rock avalanche mass were statistically analyzed. The results show that: (1) Under the effect of gravity, the internal structural joints of the rock avalanche rapidly interconnected, dividing the avalanche mass into numerous fragmented blocks that eventually slid along the down-dip joint surfaces. (2) The collapse exhibited significant fragmentation phenomena in the entire movement process, with extensive disintegration during the initial failure and friction-induced tearing and cracking fragmentation during the accumulation stage. (3) The feret’s diameter distribution curves of the fragments at different time intervals were fitted using Weibull two-parameter distribution model and fractal geometry theory. The results showed that the fragmentation degree of the avalanche during the accumulation stage (t = 21.7 to 72.4 s) was weaker than that during the initial failure stage (t = 0 to 21.7 s). The fractal dimension of the fragments and the proportion of fine-grained fragments continuously increased throughout the entire movement process, once again confirming the fragmentation and disintegration phenomena during the entire process of failure and accumulation. The research findings provide a theoretical basis for revealing the dynamic fragmentation mechanism of the Zongling rock avalanche, and provide scientific guidance for the prevention and control of rock avalanche disasters in the mountainous areas of southwest China.
-
0. 引言
崩塌灾害广泛发育于中国西南地区,具有分布范围广、隐蔽性强、失稳破坏快、致灾后果严重等特点,严重威胁区域生态环境和人类活动[1 − 2]。构造节理是岩体中常见的一种结构面,其对岩体的切割作用,往往导致岩质斜坡的稳定性大幅降低,以致引发崩塌[3 − 6],同时节理的存在也会加剧崩塌发生后崩塌体在运动过程中的破碎解体[7 − 9]。鉴于构造节理对崩塌源区岩体的强烈切割作用,研究含构造节理的崩塌体运动过程中的破碎特征,对崩塌灾害预防工作将具有重要的指导意义。
目前已有大量学者通过现场监测、模型试验和数值分析等手段展开崩塌体动力破碎研究。在相关研究中,有学者注意到不同地质条件下长运移岩崩的堆积体大部分均由高度破碎的母岩组成[10 − 13]。Luo等[14]研究了头寨岩崩碎屑流中破碎体的圆度,发现高圆度是岩崩破碎体的重要特征,破碎体形状更接近立方体而非球体,并提出“大型蠕滑主滑体+低完整度锁固段”的岩质斜坡结构模式。Cagnoli等[15]通过滑槽试验研究了破碎体粒度大小对其运移距离的影响,结果表明滑动的破碎体粒度越小,其运移距离越大。Gao等[16]使用二维离散元软件分析天然边坡的地震响应和崩滑体运移过程,发现崩滑体堆积过程中,滑带附近由于破碎作用强烈,形成了由粒度逐渐细化的破碎体所组成的基底层,该基底层会减小崩滑体与滑带间的摩擦,促进堆积体的流动。Dunning[17]对新西兰以及瑞士境内的5处崩塌堆积体的岩块粒径进行统计,提出崩塌堆积过程中高度破碎体的粒度分布符合分形、自相似规律。实际上,受限于动力条件下岩体裂纹扩展模拟的复杂性,当前关于含构造节理崩塌的破碎特征研究主要依靠对崩塌结束后现场堆积体的观测,因而难以分析崩塌运动全过程的破碎情况;此外,一些基于数值模拟手段分析崩塌体动力破碎的研究,因无法直接获得破碎体的粒径信息,而只能通过归一化的等效粒径对破碎体进行分析,以致无法直观地监测破碎体真实粒径的变化,所以当前对崩塌动力破碎的认识或研究仍有待进一步深化。
近年来,PFC颗粒流离散元方法展现了其在模拟岩土微观裂纹及宏观大变形破坏等领域的优势[18-19],逐渐成为国内外岩土灾害研究领域的有力手段。本文通过PFC对贵州省毕节市纳雍县鬃岭崩塌进行数值研究,通过单轴压缩数值试验标定了一组合适的接触模型参数,再根据所建立的PFC二维崩塌模型,重点分析该崩塌体破坏及堆积过程中的动力破碎现象,并引入颗粒学中具有真实物理尺度特点的最大弗雷特直径(feret’s diameter)代替归一化的等效粒径来表征破碎体的粒度,随后利用双参数Weibull分布模型以及分形维数对统计得到的破碎体粒径信息进行分析,研究结果为大型崩塌体动力破碎的相关研究提供了理论依据,对西南地区崩塌地质灾害的防治工作也有一定指导意义。
1. 研究区概况
1.1 地形地貌
纳雍县鬃岭镇位于云贵高原向黔中山原的过度地带,属于溶蚀-侵蚀中山地貌区。鬃岭镇西北部为马鬃岭中山区,海拔2200~2300 m。中岭边坡位于马鬃岭中山区之内,其坡顶高程为 2 331.5 m,边坡东南侧陡坡以下地势呈阶梯状,其地形地貌见图1(a)(c),其中一级平台高程为2005~2025 m,最大宽度近200 m;二级平台的高程为1980~1990 m,鬃岭镇位于二级平台上;三级平台的高程约1960 m。
1.2 地质条件
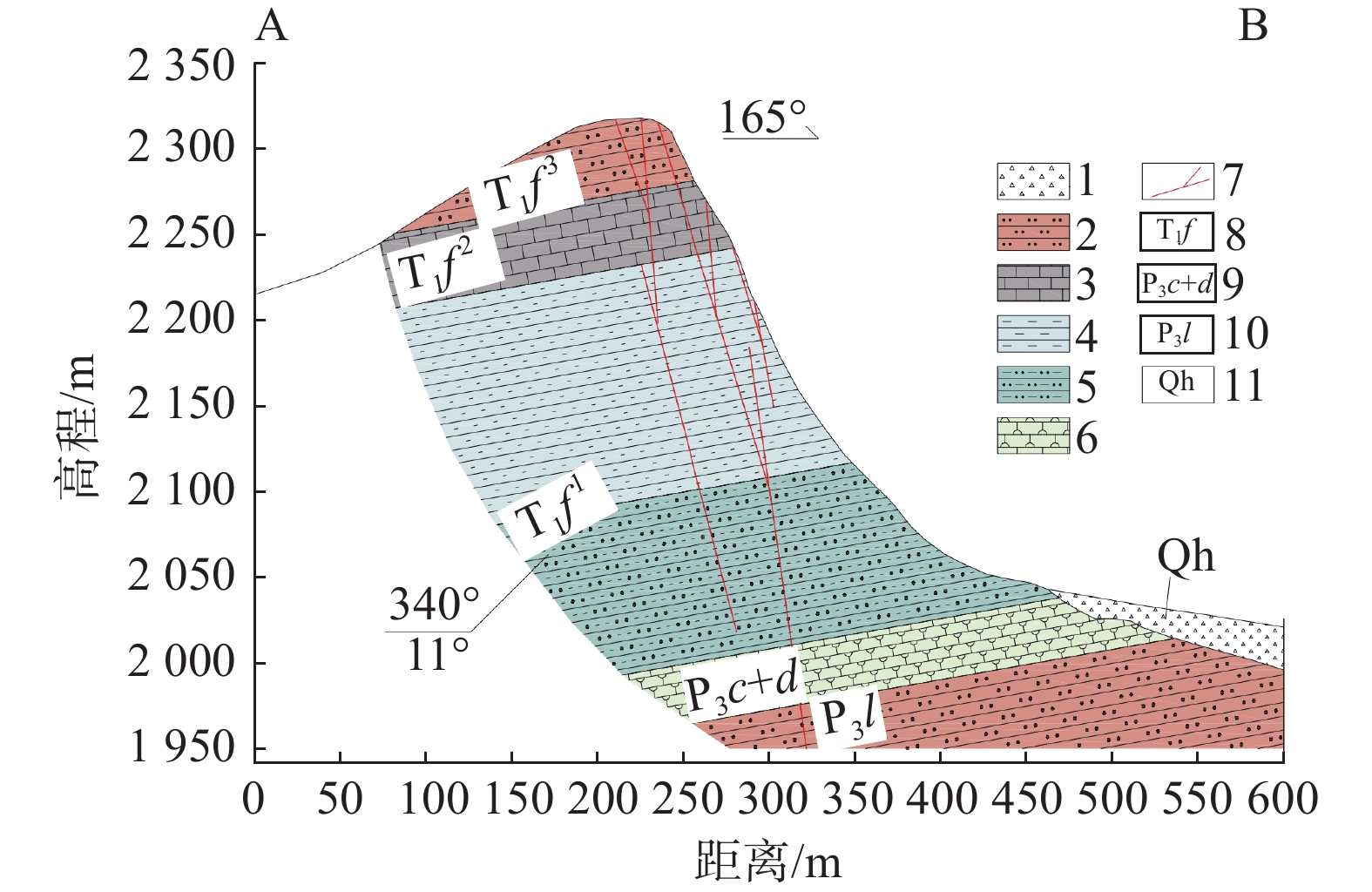
根据水文地质勘测资料,中岭边坡出露的地层岩组主要包括第四系(Qh)、下三叠统飞仙关组(T1f)、上二叠统长兴-大隆组(P3c+d)以及上二叠统龙潭组(P3l),其中飞仙关组主要分布于中岭边坡坡顶的陡坡、陡崖;长兴-大隆组与龙潭组则主要分布于陡崖下部,见图1(b)。此外,中岭边坡地处扬子准地台中四级构造单元毕节北东向构造变形区,区内未发现断层存在。中岭边坡北翼的岩层产状为N55°~70°E/NW∠8°~15°,主要有两组节理发育,节理产状分别为N70°~80°W/NE∠75°~80°和N25°~35°E/SE∠85°;中岭边坡南翼的岩层产状为N50°~75°E/NW∠9°~18°,主要有一组节理发育,节理产状为N65°~75°E/NW∠75°~85°。
1.3 崩塌概况
2004年12月3日凌晨3时40分,贵州毕节纳雍县鬃岭镇佐家营村岩脚组孙晓煤矿突发山体崩塌,造成44人死亡。现场调查表明,此次事故由中岭边坡南翼主峰陡崖上所发育的3处不同规模的崩塌造成,分别为1#崩塌(佐家营)、2#崩塌(鬃岭)以及3#崩塌,其中2#崩塌(鬃岭)也称为鬃岭崩塌,是本文的研究对象。
据调查,鬃岭崩塌所在的中岭边坡走向为NEE,并沿走向绵延约5.3 km,边坡南翼的整体坡度约70 °。鬃岭崩塌研究区的高程范围为1990~2315 m。结合现场调查与高分卫星地图获取崩塌区域,见图1(a),随后选取沿崩塌体运动方向的剖面A-B作为建模对象,其工程地质剖面图见图2。
2. 鬃岭崩塌数值模型
2.1 微观参数标定
PFC[20]是一种常用的离散元颗粒流程序,其模型由实体(body)、接触块(piece)和接触(contact)组成。PFC对其系统内的粒间接触力学和颗粒运动学特征分别定义如下:作用在刚性实体颗粒上的力和力矩由颗粒间的柔性接触承载,并在每次循环迭代中根据接触模型框架下的力-位移定律更新粒间接触力和接触力矩。根据牛顿运动定律,使用前一次循环迭代计算所得的粒间接触力和接触力矩以及当前时间步长来更新每个实体颗粒的位置及速度。PFC程序通过不断更新颗粒间的广义力和广义位移来模拟材料的变形,突破了常规数值仿真方法分析材料大变形的局限性,为揭示微观及细观介质材料的破坏机理提供更好的手段。
线性平行黏结接触模型(linear parallel bond model)[20]常用于模拟岩石一类具有胶结特性的材料。该接触模型允许在不同实体的接触块间传递接触力和接触力矩。当材料应力超过黏结强度时,平行胶结键断裂,接触模型将退化为线性接触模型(linear model)。线性接触模型中接触界面无法抵抗相对旋转运动,只能传递接触力。所以,本文选用线性平行黏结接触模型来模拟具有胶结性质的岩石材料。
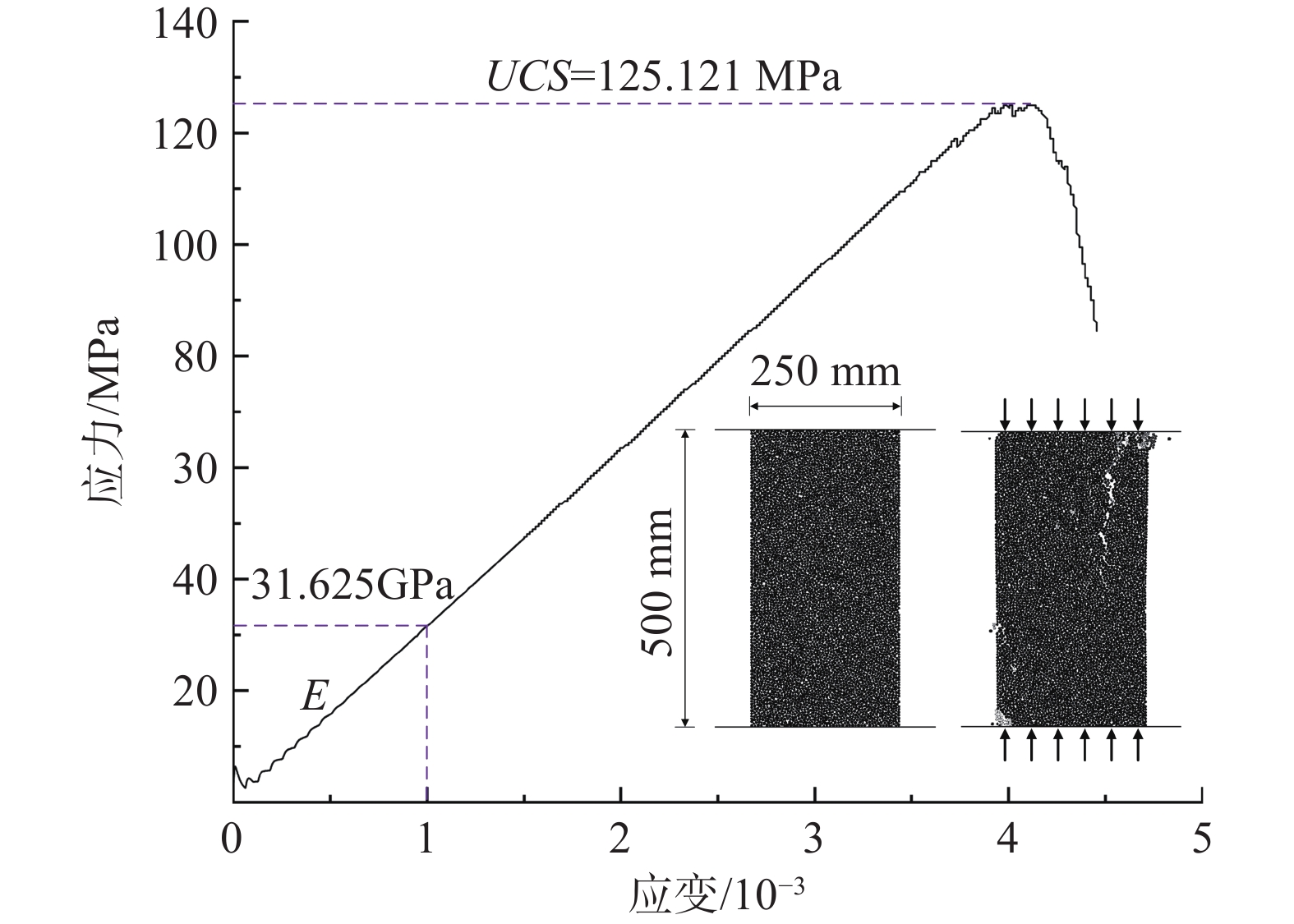
研究过程选取鬃岭镇中岭边坡区域内的灰岩样本,经室内试验测定其弹性模量(E)和单轴抗压强度(UCS)分别为E = 31.844 GPa,UCS = 128.961 MPa。室内试验测定的宏观物理力学参数不可直接用于PFC仿真过程中的参数设定,而需要进行相应的数值仿真试验来标定参数,具体过程包括使用PFC程序构建人工合成岩石试样(synthetic rock mass specimen,SRMS),再对PFC Fish Tank内置的压缩试验案例程序进行部分改进,最后通过单轴压缩数值试验对接触参数进行标定。
本次单轴压缩数值试验中,合成岩石试样尺寸设定为250 mm×500 mm,颗粒半径取值范围为2~3 mm,共随机生成5 454个颗粒。利用PFC刚性墙以及伺服程序对试样施加轴压,模拟室内岩石单轴压缩试验过程中的预压及轴向加载过程。模拟过程中,记录轴向加载下合成岩石试样的应力-应变曲线,结果见图3。最后,根据记录所得的应力-应变曲线,获得其对应PFC接触模型参数下的合成岩石试样强度参数。经不断试算,发现接触模型参数若按表1取值,模拟获得的合成岩石试样强度参数(E = 31.625 GPa,UCS = 125.121 MPa)接近室内压缩试验测定的岩体强度参数。
表 1 合成岩石试样(SRMS)微观参数Table 1. Micromechanical parameters of synthetic rock mass specimen (SRMS)关键参数名称 参数值 颗粒密度/(kg·m−3) 2 200 颗粒粒径/m 0.002~0.003 颗粒有效模量/(N·m−2) 7×109 颗粒刚度比 1.5 胶结有效模量/(N·m−2) 1.21×1010 胶结刚度比 1.5 胶结抗拉强度/(N·m−2) 8.1×108 胶结黏聚力/(N·m−2) 4.6×108 胶结内摩擦角/(°) 39.8 2.2 崩塌模型的建立
通过UAV无人机航摄获得崩塌发生后现场的三维数字高程数据(DEM),结合在商用卫星网站下载的崩塌发生前的高程数据,经ArcGIS软件处理,确定崩塌体源区范围。随后选定剖面A-B作为PFC2D数值模拟的模型区域。由于A-B剖面主要位于中岭边坡南翼的崩塌区域,所以未考虑边坡北翼的变形裂缝。根据前述边坡南翼的节理产状以及工程地质剖面图(图2)为模型设置一组构造节理与卸荷裂隙,最终所建PFC模型见图4。
3. 模拟结果分析
为了分析鬃岭崩塌运动全过程中的破碎解体情况,本文对不同运动时刻崩塌物中所含破碎体的粒径进行统计分析。离散元颗粒流中,对破碎体(fragment)的定义是指通过胶结接触连接在一起的一组实体(包括基本颗粒ball、簇clump及刚性墙wall)。在下述分析中,本文围绕PFC中定义的破碎体这一要素对不同时刻崩塌体的破碎情况进行讨论。
3.1 崩塌运动过程中的破碎特征
图5—6描述了鬃岭崩塌体在持续时长约72.4 s运动过程中的破碎体位置及粒径分布情况。可以发现,t = 0.4 s时坡体内的破碎作用主要发生在边坡顶部交叉节理附近的位置,破碎规模很小,初步形成整体相对稳定的危岩带。
t = 2.9 s时刻,随着坡体顶部节理附近的颗粒被进一步粉碎为散粒,由节理切割的危岩体沿结构面发生小幅位移,形成较大规模破碎体。同时,坡体临空面附近危岩体受卸荷裂隙密集切割,在重力作用下该部位破碎岩体率先脱离母岩崩落。
崩塌体的整体大规模变形主要是由崩塌体剪出口处的压剪破坏及坡顶处的拉剪破坏引起的,随着边坡顶部拉张裂缝处以及剪出口处节理裂隙附近岩体的不断破碎(t = 2.9~7.2 s),崩塌体的主滑动部分基本形成(t = 7.2 s),其主要由与坡面倾向一致的结构面前端的岩体构成。
在t = 7.2~14.5 s时刻,破碎程度较为严重的崩塌体沿顺倾的构造节理面不断向下滑落。在崩塌体下落的过程中,由于不同破碎块体间的相互碰撞及摩擦,部分粒径规模较大的块状破碎体再次发生了破碎,其破碎形式表现为大型块状破碎体沿自身中部位置的断裂、崩塌体底部破碎体与崩塌面摩擦产生的小规模破碎、崩塌体临空方向破碎体在倾倒-翻滚-碰撞作用下产生的破碎;粒径较小的破碎体则被抛洒至空中,随后下落撞击坡面,跳跃运动至崩塌体前缘。
t = 21.7 s时刻,崩塌体已基本滑动至坡脚区域,此时崩塌体的破碎情况主要表现为数量占比较高的大型块状破碎体间夹杂一些小型破碎体,同时崩塌体前缘伴有碰撞后凌空飞行的小型破碎体(岩屑)。后续t = 21.7~72.4 s时刻的崩塌体运动属于该崩塌的堆积过程。在t = 21.7 s时刻,崩塌面已经裸露出来,与边坡中发育的顺倾节理面基本一致。由图5可知,破坏过程中已破碎的崩塌体在运动至坡脚后,其在缓倾角坡面的堆积过程中仍有破碎解体现象发生。随着该模型的崩塌体逐渐耗散动能,崩塌体最终堆积在坡脚前的坡麓位置,形成半锥形的倒石堆,其崩积物中的破碎体体积、尺寸大小不一,与现场调查发现的鬃岭崩塌堆积体内的破碎体较为相似(图7)。实际上,崩塌源区岩体内节理裂隙发育比较密集,并且地层岩性复杂,加之各类风化作用对岩体的侵蚀,真实破碎体粒径相较于模拟得到的粒径偏小,但二者粒径数量级基本保持一致,满足本次数值模拟的合理容差范围。
从堆积体内不同尺寸破碎体沿水平方向的分布来看,大粒径的破碎体主要分布于堆积体中部及后缘,小粒径破碎体主要分布在堆积体前缘及其余空隙内,该分布特征与Cagnoli等[15]的研究相吻合,即粒径越小的破碎体在其运动方向上的运移距离往往更大。
3.2 破碎体信息分析
受限于PFC仿真软件只能输出破碎体的体积和位置信息,以往研究大多采用基于破碎体体积的归一化公式来计算破碎体的等效粒径,再将其用于破碎体粒径分析[16, 21 − 25]。等效粒径的计算方法为:
$$ {d}=\sqrt{{V}_{{\rm{f}}}/{V}_{0}} $$ (1) 式中:
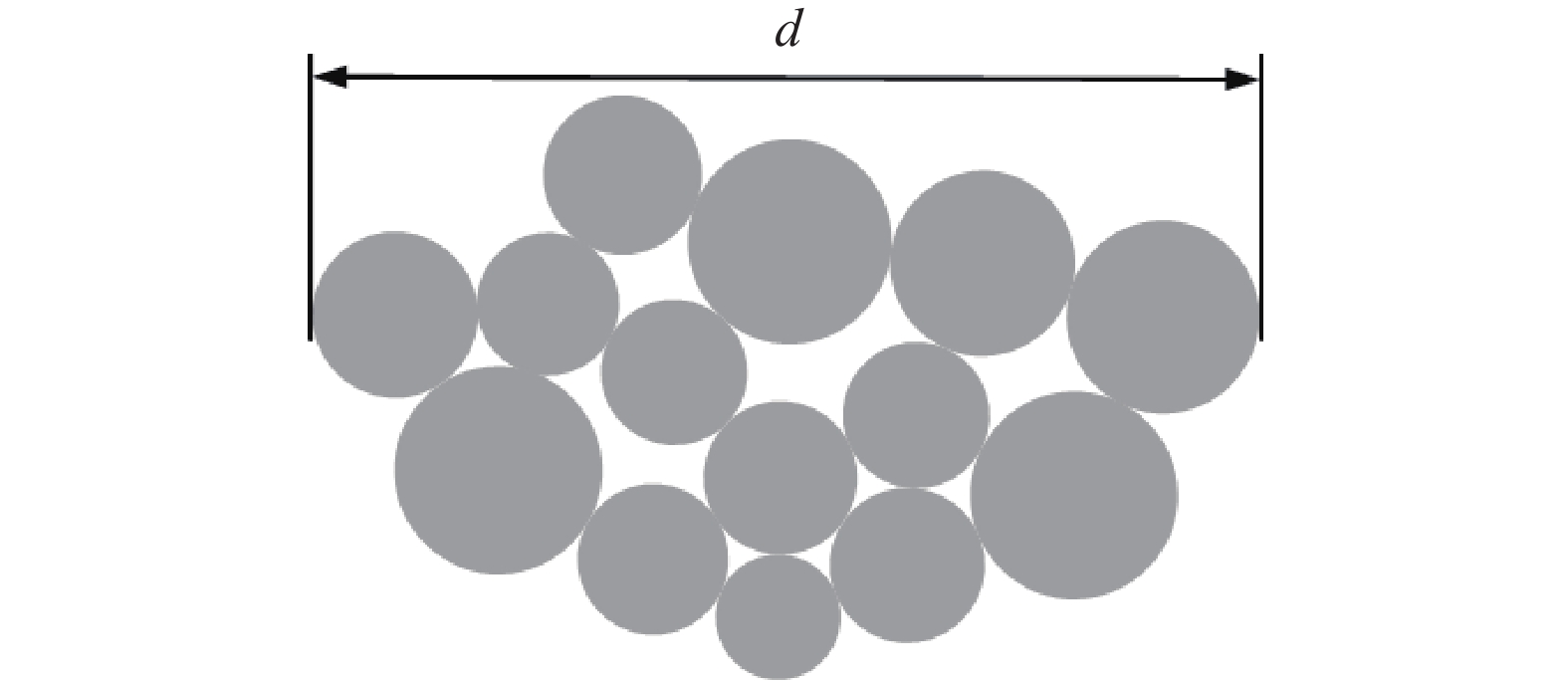
${d} $ ——破碎体的等效粒径;$ {V}_{{\rm{f}}} $ ——破碎体的体积/m3;$ {V}_{0} $ ——源区崩塌体的总体积/m3。由于等效粒径没有考虑破碎体的形状因素,以致于无法真实表征颗粒的粒度,故本文采用颗粒学中弗雷特直径(feret’s diameter)[26 − 27]的概念来表征破碎体的粒度(图8)。具体过程为:遍历崩塌体中各个破碎体所含实体颗粒的位置及半径信息,并通过冒泡排序算法[28 − 30],计算获得各破碎体中相距最远两颗粒的最大外表面间距,该间距即为最大弗雷特直径[31],本文将其作为破碎体的粒径。
目前已有大量研究使用不同分布函数来分析破碎体粒径的分布规律[32 − 34],其中双参数Weibull分布模型应用较为广泛[23 − 24, 35 − 38],本文使用该分布模型来描述崩塌体不同运动时刻的破碎体粒径分布。破碎体粒径分布的双参数Weibull模型可表示[24, 39 − 40]:
$$ {P}=1-\text{exp}\left[-{\left(\frac{{d_{\mathrm{max}}}}{{{d}}_{\text{c}}}\right)}^{\beta}\right] $$ (2) 式中:
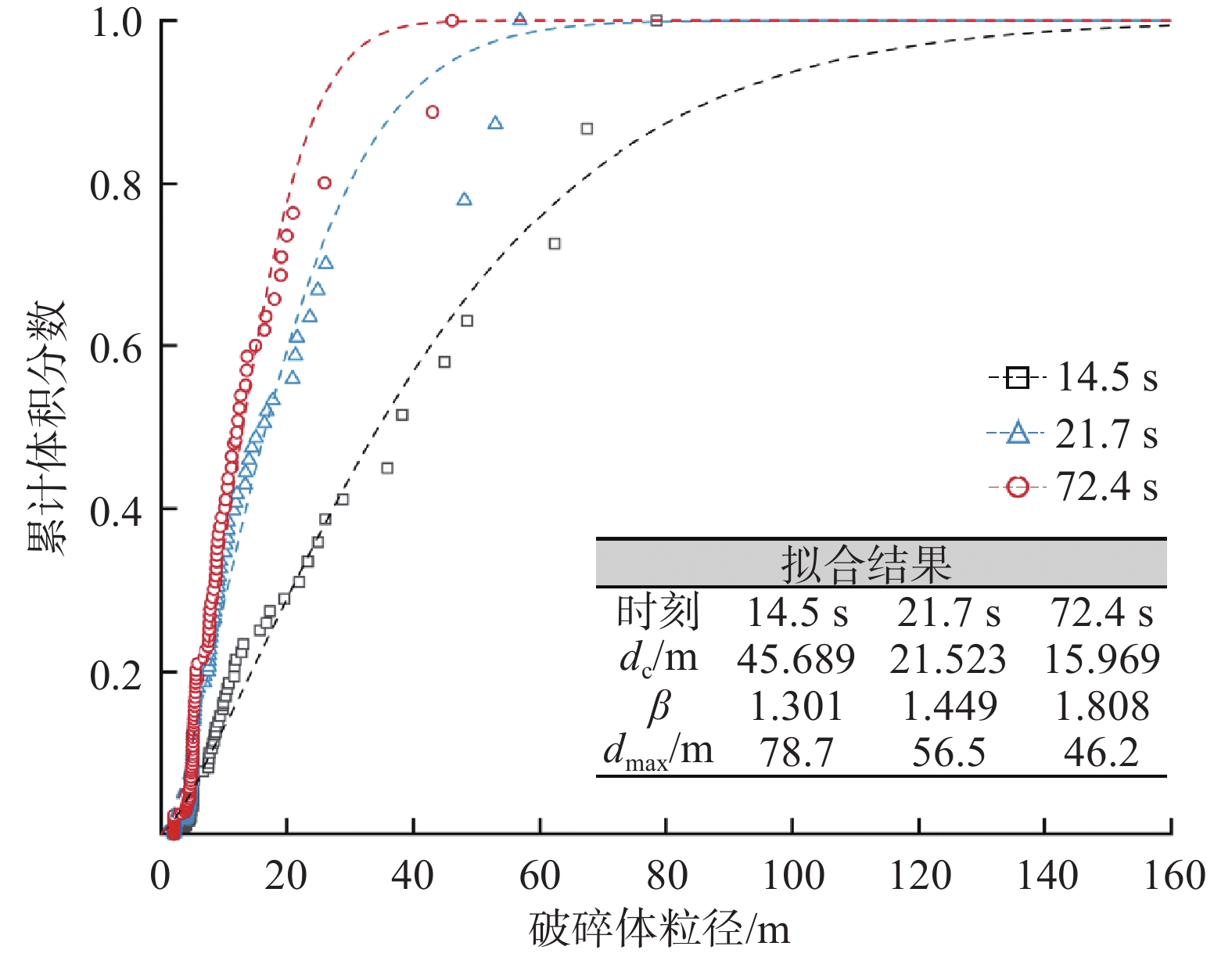
${P} $ ——累计体积分数,表示小于某一粒径的全部 破碎体体积百分含量;${d_{{\mathrm{max}}}} $ ——尺寸最大的破碎体粒径/m;$ {{d}}_{\text{c}} $ ——尺寸参数/m,对应于累计体积分数$P=1-1/{\mathrm{e}}$ 的破碎体粒径,在本文中可用于衡量破碎体中细粒径破碎体占比;$ \beta $ ——形状参数,用于表征破碎体的级配,$ \beta $ 值越大,粒径分布越窄,级配越差。基于前述不同运动阶段崩塌体的破碎情况,本文选择t = 14.5 s(破坏阶段)、t = 21.7 s(堆积阶段初期)与t = 72.4 s(堆积阶段结束)三个典型时刻的破碎体粒径信息进行分析。图9展示了不同时刻小于某一粒径破碎体累计体积分数(P)的双参数Weibull分布函数拟合结果。可见,在t = 14.5 s时刻的破碎体粒径(d)分布范围明显较大,相较于更靠后的时刻(t = 21.7 s、t = 72.4 s),崩塌体内存在更多的较大粒径破碎体。从图9不同时刻的形状参数(
$ \beta $ )也能得出这一结论,即t = 14.5 s、t = 21.7 s与t = 72.4 s时刻的形状参数($ \beta $ )依次增大,分别为1.301、1.449和1.808,可见形状参数($ \beta $ )与运动时间(t)之间的变化规律表现为正相关,反映出崩塌体内破碎体的粒径分布范围随运动时间的增加而不断变窄,相应的级配也不断变差,该结论与图5—6中的模拟结果相符合。基于上述拟合得到的破碎体尺寸参数(
$ {{}{d}}_{{{\rm{c}}}} $ )可知,t = 14.5~21.7 s堆积体中的破碎体尺寸参数($ {{d}}_{{{\rm{c}}}} $ )由45.689 m大幅减小为21.523 m,该变化表明崩塌体于破坏阶段(t = 14.5~21.7 s)的破碎程度更加剧烈,崩塌体内的细粒径破碎体占比在此期间大幅增加;而堆积阶段(t = 21.7~72.4 s)堆积体中的破碎体尺寸参数($ {{d}}_{{{\rm{c}}}} $ )则由21.523 m小幅减小至15.969 m,这表明崩塌体运动至坡脚附近时(t = 21.7 s),开始在坡脚前的缓倾角地表滑动堆积直至运动停止,堆积阶段的时间跨度较长,崩塌体内的细粒径破碎体占比增加幅度却较为有限。双参数Weibull模型的拟合结果表明,崩塌体在陡倾角坡面运动过程中破碎剧烈,而在缓倾角地表滑动堆积过程中破碎程度会减缓。动力破碎作用会存在于崩塌的整个运动过程,导致崩塌体内的细粒径破碎体不断增多,使得破碎体的粒径分布范围更为集中,级配也相应不断变差。
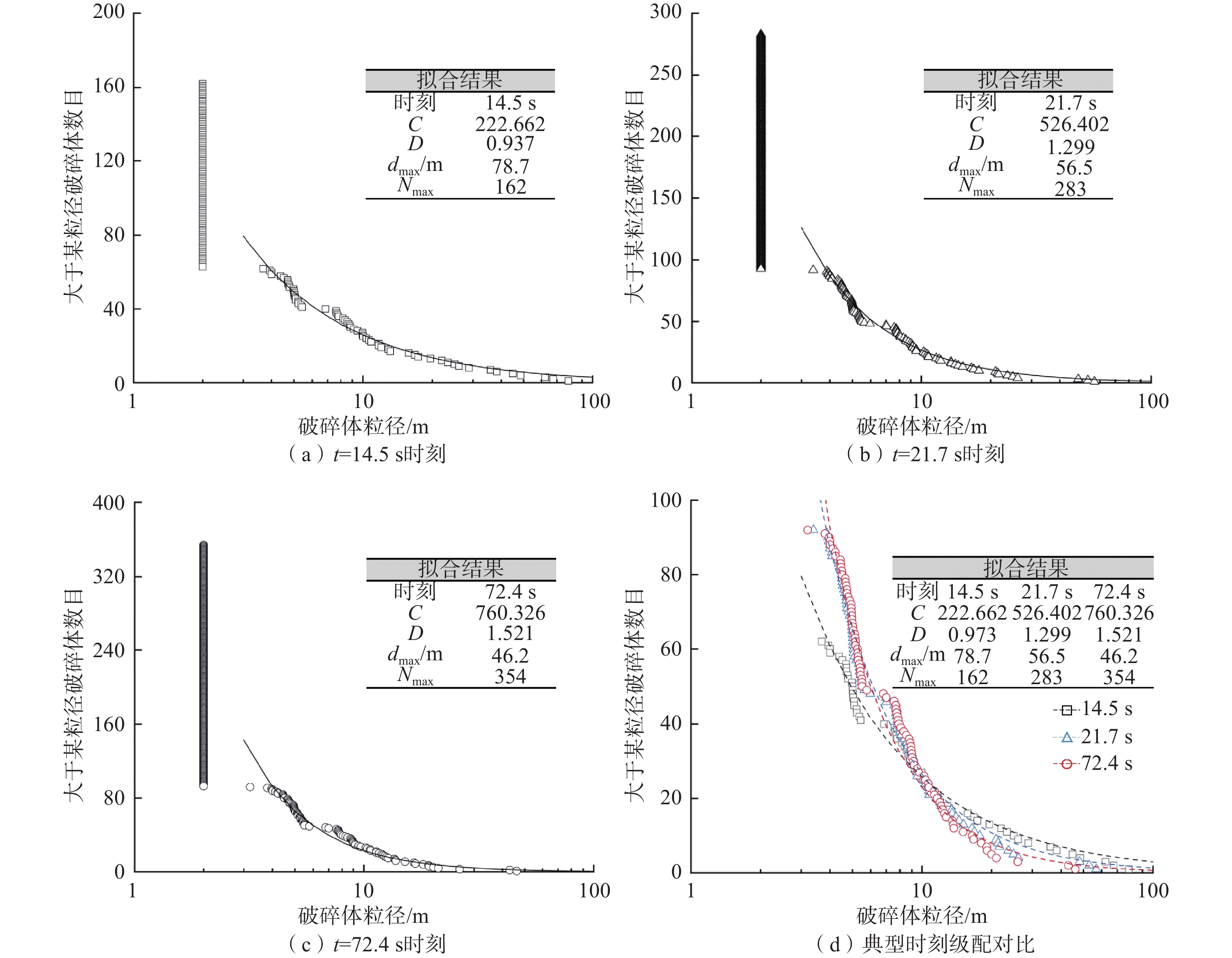
由于崩塌体运动过程中往往伴随着风化、研磨、冲击等外部作用,所以破碎体一般都会满足分形条件[41]。为了进一步探究本模型中破碎体的粒径分布规律,本文采用分形几何理论来对t = 14.5 s(崩塌破坏阶段)、t = 21.7 s(崩塌堆积阶段初期)和t = 72.4 s(崩塌堆积阶段结束)三个典型时刻的破碎体进行分析。分形特征可以由破碎体数目与粒径的幂律关系来表征[41]:
$$ {N}={C}{d}^{-{D}} $$ (3) 式中:
${N} $ ——破碎体数目;$ {C} $ ——比例常数;${d} $ ——破碎体的粒径/m;$ {D} $ ——分形维数,其值越大,破碎体破碎程度越高。由于PFC自身特性,导致部分母破碎体解体为基本颗粒后无法进一步破碎,此时的基本颗粒被PFC系统判定为已完全破碎的子破碎体。本文仍以前述3个典型时刻分析破碎体的分形规律,在筛除基本颗粒后,拟合得到各时刻破碎体的粒径(d)-数目(N)级配曲线(图10)。其中,t = 14.5 s、t = 21.7 s和t = 72.4 s时刻破碎体最大数目(
$ {{N}}_{\text{max}} $ )分别为162、283和354,破碎体的分形维数($ D $ )分别为0.937、1.299和1.521。可以看到,崩塌体在破坏阶段(t = 14.5~21.7 s)解体增加的破碎体数目相比于堆积阶段(t = 21.7~72.4 s)更多。分形维数的变化表明在破坏及堆积阶段(t = 14.5~72.4 s)大粒径破碎体随着整个崩塌物的运移发生了进一步破碎,破碎体粒径的离差程度不断减小,分选性变得更好。根据图10(d)中不同典型时刻破碎体粒径-数目级配曲线的比对结果,t = 21.7 s与t = 72.4 s时刻的拟合曲线以及大粒径破碎体散点分布均较为接近,表明堆积阶段(t = 21.7~72.4 s)崩塌物中大粒径破碎体的动力破碎趋于稳定,对应了前述基于双参数Weibull分布函数分析得出的结论,即堆积过程中崩塌物破碎剧烈程度会不断减缓直至运动停止。上述两种破碎体粒径的统计分析结果,均在一定程度上论证了此类崩塌体在陡倾角坡面及缓倾角地表运动中的动力破碎现象。
4. 讨论
事实上,弗雷特直径体系包含有:最大(小)弗雷特直径、等效矩形弗雷特长(短)径和等效椭圆弗雷特长(短)径等。根据Luo等[14]的研究,岩崩破碎体的形状更接近立方体而非球体,选取等效矩形弗雷特长径表征粒径理论上结果将更加精准;另外有研究认为,对于某些形心处于破碎体边界外的凹形破碎体,最小弗雷特直径、等效矩形弗雷特短径更适合作为粒径[42]。然而本文仅采用最大弗雷特直径来表征破碎体粒径,是基于以下两点考虑:(1)在PFC中,破碎体的等效矩形弗雷特长(短)径获取方式较为复杂,需要按照角度增量为1°设置至少360组环绕破碎体外表面并与其相切的辅助线,随后遍历破碎体中各边界颗粒表面与该辅助线间的距离,其中距离最大值为等效矩形弗雷特长径,距离最小值为等效矩形弗雷特短径。相比于等效矩形弗雷特长(短)径,最大弗雷特直径的获取仅需要遍历各破碎体中颗粒间的最大直线距离即可。考虑到崩塌数值模拟过程中往往会形成数以千计的破碎体,使用最大弗雷特直径可以显著提高PFC的计算效率。因此,等效矩形弗雷特长(短)径的适用工况应为破碎体总数较少,且数据精细程度要求较高的对象,例如落石灾害。(2) Igathinathane等[42]的研究结果表明最小弗雷特直径、等效矩形弗雷特短径更适合用于表征形心处于破碎体边界外的凹形破碎体粒径。而图5—6均显示本模型的崩塌体运动全过程中破碎体大多为非凹形状,且比较接近矩形。因此,最小弗雷特直径、等效矩形弗雷特短径和等效椭圆弗雷特长(短)径并不适合表征崩塌破碎体粒径。
本文中破碎体的“反粒序结构”行为并不明显,原因在于两点:(1)“反粒序结构”行为大多出现在高速远程滑坡所形成的滑坡-碎屑流堆积体中,其形成原因主要为碎屑流运动路径上因滑面不规则起伏所引发的振动筛分作用和滑体碎屑颗粒之间碰撞所产生的动力破碎作用以及二者的耦合过程[43]。根据图5—6,鬃岭崩塌堆积体最远运动距离较短(约200 m),导致堆积过程中的破碎程度不及高速远程滑坡充分,堆积体底部的破碎体未被进一步研磨解体[44 − 46]。(2)鬃岭崩塌源区岩体中节理、裂隙分布的形状及密度相较于本模型更为复杂且密集,因此本模型中破碎体难以达到现场堆积体的破碎程度,这也解释了前述分析中模型破碎体的最大弗雷特直径比真实破碎体粒径稍偏大的计算结果。
5. 结论
(1)鬃岭崩塌的破坏模式可归纳为:岩体沿节理被分割成不同的块体—坡脚压剪作用及坡肩拉剪作用同时发生—顺倾节理面前方崩塌主体形成—崩塌体沿顺倾节理面滑下。
(2)鬃岭崩塌在前期破坏及后续崩塌体堆积过程中,均存在明显的破碎现象。具体表现为崩塌体在破坏阶段(t = 0~21.7 s)集中于陡倾角崩塌面的大范围破碎解体,与堆积阶段(t = 21.7~72.4 s)集中于缓倾角地表的摩擦拉裂破碎。整个运动过程中崩塌体一直伴随有子破碎体的产生以及母破碎体的解体消失。
(3)根据双参数Weibull分布模型及分形几何理论拟合的不同时刻的破碎体粒径分布结果表明:崩塌体在破坏阶段的破碎程度较堆积阶段更为剧烈,并且破坏阶段崩塌体内部的破碎体粒径分布范围较广(最大弗雷特直径2~100 m);堆积过程中的崩塌体虽然破碎程度较轻,但仍处于破碎的状态(破碎体的分形维数不断增大),此时崩塌堆积体内的细粒径破碎体不断增多,粒径分布范围逐渐变窄(最大弗雷特直径2~50 m)。
-
表 1 合成岩石试样(SRMS)微观参数
Table 1 Micromechanical parameters of synthetic rock mass specimen (SRMS)
关键参数名称 参数值 颗粒密度/(kg·m−3) 2 200 颗粒粒径/m 0.002~0.003 颗粒有效模量/(N·m−2) 7×109 颗粒刚度比 1.5 胶结有效模量/(N·m−2) 1.21×1010 胶结刚度比 1.5 胶结抗拉强度/(N·m−2) 8.1×108 胶结黏聚力/(N·m−2) 4.6×108 胶结内摩擦角/(°) 39.8 -
[1] 铁永波,徐伟,向炳霖,等. 西南地区地质灾害风险“点面双控” 体系构建与思考[J]. 中国地质灾害与防治学报,2022,33(3):106 − 113. [TIE Yongbo, XU Wei,XIANG Binglin,et al. The thoughts on construction of “double-control of point and zone” system of geological hazard risk in southwest China[J]. The Chinese Journal of Geological Hazard and Control,2022,33(3):106 − 113. (in Chinese with English abstract)] TIE Yongbo, XU Wei, XIANG Binglin, et al. The thoughts on construction of “double-control of point and zone” system of geological hazard risk in southwest China[J]. The Chinese Journal of Geological Hazard and Control, 2022, 33(3): 106 − 113. (in Chinese with English abstract)
[2] 张恩铭,程谦恭,林棋文,等. 岩体结构对岩质滑坡运动过程和堆积特征的影响研究[J]. 水文地质工程地质,2022,49(3):125 − 135. [ZHANG Enming,CHENG Qiangong,LIN Qiwen,et al. A Study of the influence of rock mass structure on the propagation processes and deposit characteristics of rockslides[J]. Hydrogeology & Engineering Geology,2022,49(3):125 − 135. (in Chinese with English abstract)] ZHANG Enming, CHENG Qiangong, LIN Qiwen, et al. A Study of the influence of rock mass structure on the propagation processes and deposit characteristics of rockslides[J]. Hydrogeology & Engineering Geology, 2022, 49(3): 125 − 135. (in Chinese with English abstract)
[3] 陈鹏宇. 岩质高边坡坡体结构特征分析与稳定性研究——以焦作市龙寺矿山岩质高边坡为例[D]. 武汉:中国地质大学,2015. [CHEN Pengyu. Structural characteristics analysis and stability study of high rock slope:A case study of Longsi mine in Jiaozuo City[D]. Wuhan:China University of Geosciences,2015. (in Chinese with English abstract)] CHEN Pengyu. Structural characteristics analysis and stability study of high rock slope: A case study of Longsi mine in Jiaozuo City[D]. Wuhan: China University of Geosciences, 2015. (in Chinese with English abstract)
[4] 贺续文,刘忠,廖彪,等. 基于离散元法的节理岩体边坡稳定性分析[J]. 岩土力学,2011,32(7):2199 − 2204. [HE Xuwen,LIU Zhong,LIAO Biao,et al. Stability analysis of jointed rock slopes based on discrete element method[J]. Rock and Soil Mechanics,2011,32(7):2199 − 2204. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1000-7598.2011.07.046 HE Xuwen, LIU Zhong, LIAO Biao, et al. Stability analysis of jointed rock slopes based on discrete element method[J]. Rock and Soil Mechanics, 2011, 32(7): 2199 − 2204. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-7598.2011.07.046
[5] HE Lei,AN Xinmei,MA Guowei,et al. Development of three-dimensional numerical manifold method for jointed rock slope stability analysis[J]. International Journal of Rock Mechanics and Mining Sciences,2013,64:22 − 35. DOI: 10.1016/j.ijrmms.2013.08.015
[6] AN Xinmei,NING Youjun,MA Guowei,et al. Modeling progressive failures in rock slopes with non-persistent joints using the numerical manifold method[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2014,38(7):679 − 701. DOI: 10.1002/nag.2226
[7] 李连崇,唐春安,邢军,等. 节理岩质边坡变形破坏的RFPA模拟分析[J]. 东北大学学报,2006,27(5):559 − 562. [LI Lianchong,TANG Chunan,XING Jun,et al. Numerical simulation and analysis of deformation and failure of jointed rock slopes by RFPA-slope[J]. Journal of Northeastern University (Natural Science),2006,27(5):559 − 562. (in Chinese with English abstract)] LI Lianchong, TANG Chunan, XING Jun, et al. Numerical simulation and analysis of deformation and failure of jointed rock slopes by RFPA-slope[J]. Journal of Northeastern University (Natural Science), 2006, 27(5): 559 − 562. (in Chinese with English abstract)
[8] 张秀丽. 断续节理岩体破坏过程的数值分析方法研究[D]. 武汉:中国科学院研究生院(武汉岩土力学研究所),2007. [ZHANG Xiuli. Study on numerical analysis method of failure process of discontinuous jointed rock mass[D]. Wuhan:Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2007. (in Chinese with English abstract)] ZHANG Xiuli. Study on numerical analysis method of failure process of discontinuous jointed rock mass[D]. Wuhan: Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, 2007. (in Chinese with English abstract)
[9] 王博. 破碎岩石边坡动力稳定性及抗震加固研究[D]. 重庆:重庆交通大学,2020. [WANG Bo. Study on dynamic stability and seismic reinforcement of broken rock slope[D]. Chongqing:Chongqing Jiaotong University,2020. (in Chinese with English abstract)] WANG Bo. Study on dynamic stability and seismic reinforcement of broken rock slope[D]. Chongqing: Chongqing Jiaotong University, 2020. (in Chinese with English abstract)
[10] LOCAT P,COUTURE R,LEROUEIL S,et al. Fragmentation energy in rock avalanches[J]. Canadian Geotechnical Journal,2006,43(8):830 − 851. DOI: 10.1139/t06-045
[11] CROSTA G B,FRATTINI P,FUSI N. Fragmentation in the val pola rock avalanche,Italian Alps[J]. Journal of Geophysical Research,2007,112(F1):F01006.
[12] PERINOTTO H,SCHNEIDER J L,BACHÈLERY P,et al. The extreme mobility of debris avalanches:A new model of transport mechanism[J]. Journal of Geophysical Research:Solid Earth,2015,120(12):8110 − 8119. DOI: 10.1002/2015JB011994
[13] WANG Yufeng,CHENG Qiangong,ZHU Qi. Surface microscopic examination of quartz grains from rock avalanche basal facies[J]. Canadian Geotechnical Journal,2015,52(2):167 − 181. DOI: 10.1139/cgj-2013-0284
[14] LUO Junyao,XU Zemin,REN Zhe,et al. Rock avalanche-debris geometry and implications for rock-avalanche genesis[J]. Geomorphology,2019,334:60 − 75. DOI: 10.1016/j.geomorph.2019.02.029
[15] CAGNOLI B,ROMANO G P. Effect of grain size on mobility of dry granular flows of angular rock fragments:An experimental determination[J]. Journal of Volcanology and Geothermal Research,2010,193(1/2):18 − 24.
[16] GAO Ge,MEGUID M A,CHOUINARD L E,et al. Insights into the transport and fragmentation characteristics of earthquake-induced rock avalanche:Numerical study[J]. International Journal of Geomechanics,2020,20(9):04020157.
[17] DUNNING S A. The grain size distribution of rock- avalanche deposits in valley-confined settings[J]. Italian Journal of Engineering Geology and Environment,2006(1):117 − 121.
[18] 常文斌,王平,于一帆,等. 颗粒离散元模拟边坡动力响应的研究进展[J]. 水利与建筑工程学报,2021,19(2):48 − 53. [CHANG Wenbin,WANG Ping,YU Yifan,et al. Research progress of the slope dynamic response simulation by particle discrete elements method[J]. Journal of Water Resources and Architectural Engineering,2021,19(2):48 − 53. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1672-1144.2021.02.009 CHANG Wenbin, WANG Ping, YU Yifan, et al. Research progress of the slope dynamic response simulation by particle discrete elements method[J]. Journal of Water Resources and Architectural Engineering, 2021, 19(2): 48 − 53. (in Chinese with English abstract) DOI: 10.3969/j.issn.1672-1144.2021.02.009
[19] WANG Jing,WANG Chao,XIE Chou,et al. Monitoring of large-scale landslides in Zongling,Guizhou,China,with improved distributed scatterer interferometric SAR time series methods[J]. Landslides,2020,17(8):1777 − 1795. DOI: 10.1007/s10346-020-01407-5
[20] CUNDALL P A. A computer model for simulating progressive,large scale movement in blocky rock systems[J]. Symp. ISRM,Nancy,France,Proc,1971:2.
[21] GAO Ge,MEGUID M A,CHOUINARD L E,et al. Dynamic disintegration processes accompanying transport of an earthquake-induced landslide[J]. Landslides,2021,18(3):909 − 933. DOI: 10.1007/s10346-020-01508-1
[22] CHEONG Y S,SALMAN A D,HOUNSLOW M J. Effect of impact angle and velocity on the fragment size distribution of glass spheres[J]. Powder Technology,2003,138(2/3):189 − 200.
[23] PALUSZNY A,TANG Xuhai,NEJATI M,et al. A direct fragmentation method with Weibull function distribution of sizes based on finite- and discrete element simulations[J]. International Journal of Solids and Structures,2016,80:38 − 51. DOI: 10.1016/j.ijsolstr.2015.10.019
[24] CHEONG Y S,REYNOLDS G K,SALMAN A D,et al. Modelling fragment size distribution using two-parameter Weibull equation[J]. International Journal of Mineral Processing,2004,74:S227 − S237. DOI: 10.1016/j.minpro.2004.07.012
[25] SHEN Weigang,ZHAO Tao,CROSTA G B,et al. Analysis of impact-induced rock fragmentation using a discrete element approach[J]. International Journal of Rock Mechanics and Mining Sciences,2017,98:33 − 38. DOI: 10.1016/j.ijrmms.2017.07.014
[26] 王有鹏,李德文,王锦鹏. 金沙江巧家段冲积物动态图像法粒度特征研究[J]. 地质论评,2019,65(2):503 − 513. [WANG Youpeng,LI Dewen,WANG Jinpeng. Analysis on grain size of alluvial sediments in the Qiaojia segment,Upper Yangtze River,based on dynamic image method[J]. Geological Review,2019,65(2):503 − 513. (in Chinese with English abstract)] DOI: 10.16509/j.georeview.2019.02.019 WANG Youpeng, LI Dewen, WANG Jinpeng. Analysis on grain size of alluvial sediments in the Qiaojia segment, Upper Yangtze River, based on dynamic image method[J]. Geological Review, 2019, 65(2): 503 − 513. (in Chinese with English abstract) DOI: 10.16509/j.georeview.2019.02.019
[27] 陈泽琦,范伟军,郭斌,等. 基于形态重建和反向跟踪的粗集料级配视觉检测[J]. 计量学报,2021,42(6):710 − 717. [CHEN Zeqi,FAN Weijun,GUO Bin,et al. A visual detection method for particle size of moving coarse aggregate based on morphological reconstruction and reverse tracking[J]. Acta Metrologica Sinica,2021,42(6):710 − 717. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1000-1158.2021.06.04 CHEN Zeqi, FAN Weijun, GUO Bin, et al. A visual detection method for particle size of moving coarse aggregate based on morphological reconstruction and reverse tracking[J]. Acta Metrologica Sinica, 2021, 42(6): 710 − 717. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-1158.2021.06.04
[28] WANG Min. Analysis on bubble sort algorithm optimization[C]//2010 International Forum on Information Technology and Applications. July 16 − 18,2010,Kunming,China. IEEE,2010:208 − 211.
[29] CLIFFORD A. 数据结构与算法分析:C++版[M]. 北京:电子工业出版社,2010. [CLIFFORD A. Practical introduction to data structures and algorithm analysis[M]. Beijing:Publishing House of Electronics Industry,2010. (in Chinese with English abstract)] CLIFFORD A. Practical introduction to data structures and algorithm analysis[M]. Beijing: Publishing House of Electronics Industry, 2010. (in Chinese with English abstract)
[30] ZHANG Jian,JIN Rui. An improved bubble sort method - marking bubble sort[C]//The International Conference on Cyber Security Intelligence and Analytics. Cham:Springer,2021:862 − 868.
[31] WALTON W H. Feret‘s statistical diameter as a measure of particle size[J]. Nature,1948,162(4113):329 − 330.
[32] EPSTEIN B. The mathematical description of certain breakage mechanisms leading to the logarithmico-normal distribution[J]. Journal of the Franklin Institute,1947,244(6):471 − 477. DOI: 10.1016/0016-0032(47)90465-1
[33] ROSIN P. Laws governing the fineness of powdered coal[J]. Journal of Institute of Fuel,1933,7:29 − 36.
[34] MOTT N F,LINFOOT E H. A theory of fragmentation[M]// Fragmentation of Rings and Shells. Berlin,Heidelberg:Springer,2006:207 − 225.
[35] PALUSZNY A,TANG X H,ZIMMERMAN R W. Fracture and impulse based finite-discrete element modeling of fragmentation[J]. Computational Mechanics,2013,52(5):1071 − 1084. DOI: 10.1007/s00466-013-0864-5
[36] MCSAVENEY M J. Recent rockfalls and rock avalanches in mount cook National Park,new zealand[C]//Reviews in Engineering Geology. 2002,15:Geological Society of America,2002:35 − 70.
[37] MA Gang,ZHOU Wei,REGUEIRO R A,et al. Modeling the fragmentation of rock grains using computed tomography and combined FDEM[J]. Powder Technology,2017,308:388 − 397. DOI: 10.1016/j.powtec.2016.11.046
[38] SALMAN A D,HOUNSLOW M J,VERBA A. Particle fragmentation in dilute phase pneumatic conveying[J]. Powder Technology,2002,126(2):109 − 115. DOI: 10.1016/S0032-5910(02)00048-7
[39] WEIBULL W. A statistical distribution function of wide applicability[J]. Journal of Applied Mechanics,1951,18(3):293 − 297. DOI: 10.1115/1.4010337
[40] CARMONA H A,WITTEL F K,KUN F,et al. Fragmentation processes in impact of spheres[J]. Physical Review E,Statistical,Nonlinear,and Soft Matter Physics,2008,77(5):051302.
[41] TURCOTTE D L. Fractals and fragmentation[J]. Journal of Geophysical Research,1986,91(B2):1921. DOI: 10.1029/JB091iB02p01921
[42] IGATHINATHANE C,MELIN S,SOKHANSANJ S,et al. Machine vision based particle size and size distribution determination of airborne dust particles of wood and bark pellets[J]. Powder Technology,2009,196(2):202 − 212. DOI: 10.1016/j.powtec.2009.07.024
[43] 王玉峰,程谦恭,朱圻. 汶川地震触发高速远程滑坡-碎屑流堆积反粒序特征及机制分析[J]. 岩石力学与工程学报,2012,31(6):1089 − 1106. [WANG Yufeng,CHENG Qiangong,ZHU Qi. Inverse grading analysis of deposit from rock avalanches triggered by Wenchuan earthquake[J]. Chinese Journal of Rock Mechanics and Engineering,2012,31(6):1089 − 1106. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1000-6915.2012.06.002 WANG Yufeng, CHENG Qiangong, ZHU Qi. Inverse grading analysis of deposit from rock avalanches triggered by Wenchuan earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(6): 1089 − 1106. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-6915.2012.06.002
[44] 王明辉,曹熙平,谯立家. 危岩体精细调查与崩塌过程三维场景模拟——以西南某水电站高边坡为例[J]. 中国地质灾害与防治学报,2023,34(6):86 − 96. [WANG Minghui,CAO Xiping,QIAO Lijia. Comprehensive analysis of hazardous rock mass and simulation of potential rockfall processes using 3D terrain model:A case study of the high cut slope near damsite of a hydropower station in Southern China[J]. The Chinese Journal of Geological Hazard and Control,2023,34(6):86 − 96. (in Chinese with English abstract)] WANG Minghui, CAO Xiping, QIAO Lijia. Comprehensive analysis of hazardous rock mass and simulation of potential rockfall processes using 3D terrain model: A case study of the high cut slope near damsite of a hydropower station in Southern China[J]. The Chinese Journal of Geological Hazard and Control, 2023, 34(6): 86 − 96. (in Chinese with English abstract)
[45] 刘鑫, 董广阳, 史旦达. 考虑颗粒破碎的砂土中鱼雷锚贯入离散元分析[J]. 水文地质工程地质,2024,51(1):91 − 101. [LIU Xin, DONG Guangyang, SHI Danda. Discrete element analysis of torpedo anchor penetration into calcareous sands considering particle breakage[J]. Hydrogeology & Engineering Geology,2024,51(1):91 − 101. (in Chinese with English abstract)] LIU Xin, DONG Guangyang, SHI Danda. Discrete element analysis of torpedo anchor penetration into calcareous sands considering particle breakage[J]. Hydrogeology & Engineering Geology, 2024, 51(1): 91 − 101. (in Chinese with English abstract)
[46] 孔祥曌, 李滨, 贺凯, 等. 柱状岩体崩塌动力特征与破碎规律——以重庆甑子岩崩塌为例[J]. 中国地质灾害与防治学报,2022,33(5):1 − 10. [KONG Xiangzhao, LI Bin, HE Kai, et al. Dynamic characteristics and fragmentation evolution of columnar rockfall: A case study of the Zengziyan rockfall in Chongqing, China[J]. The Chinese Journal of Geological Hazard and Control,2022,33(5):1 − 10. (in Chinese with English abstract)] KONG Xiangzhao, LI Bin, HE Kai, et al. Dynamic characteristics and fragmentation evolution of columnar rockfall: A case study of the Zengziyan rockfall in Chongqing, China[J]. The Chinese Journal of Geological Hazard and Control, 2022, 33(5): 1 − 10. (in Chinese with English abstract)





 下载:
下载:




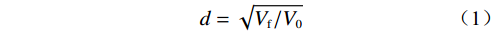
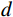
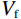
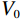
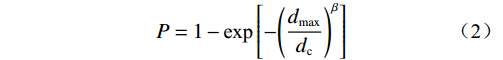
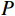
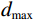
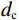
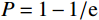
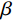
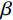
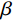
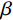
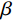
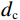
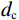
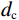
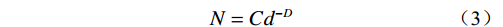
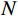

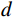
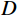
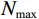
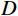
 邮件订阅
邮件订阅 RSS
RSS