Research on prediction model of landslide creep displacement on genetic algorithm
-
摘要:
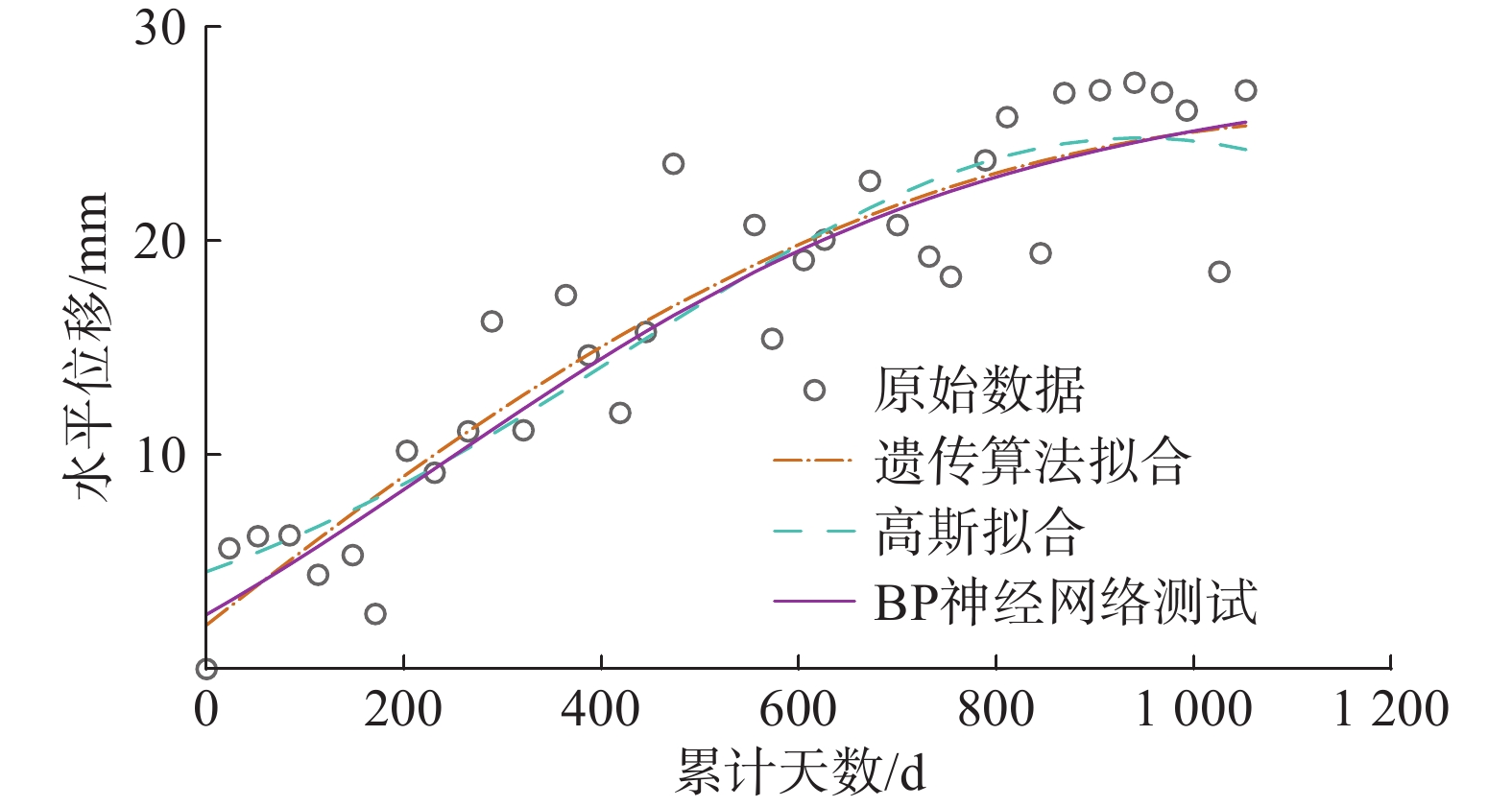
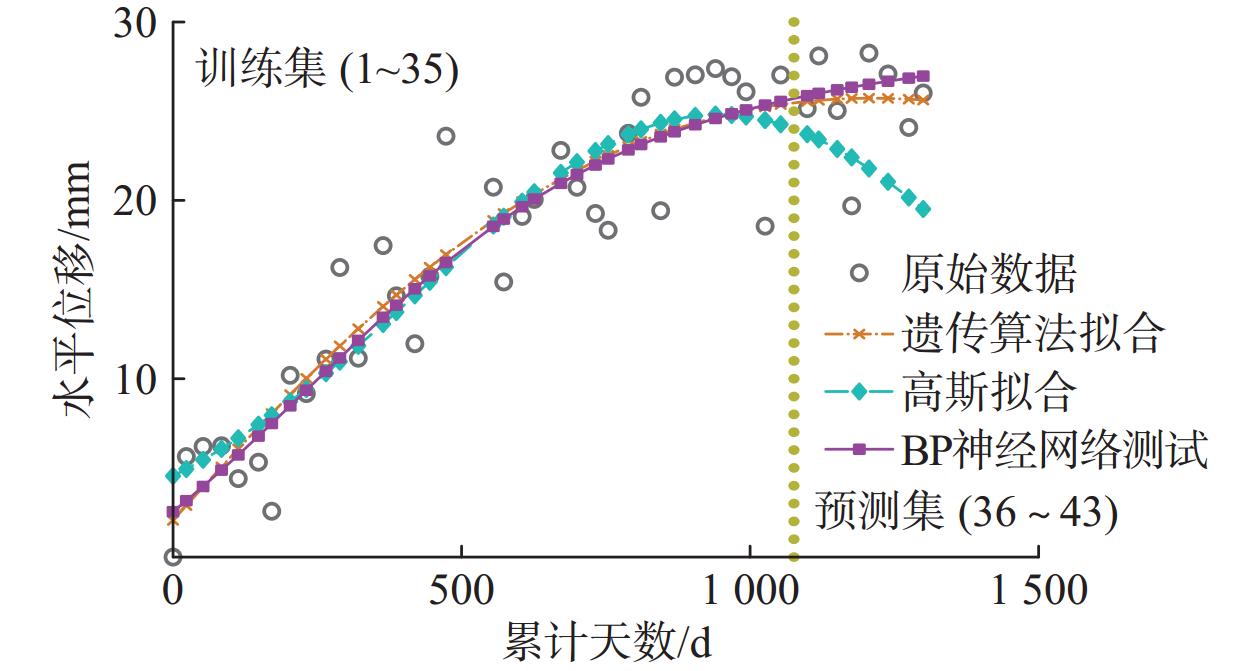
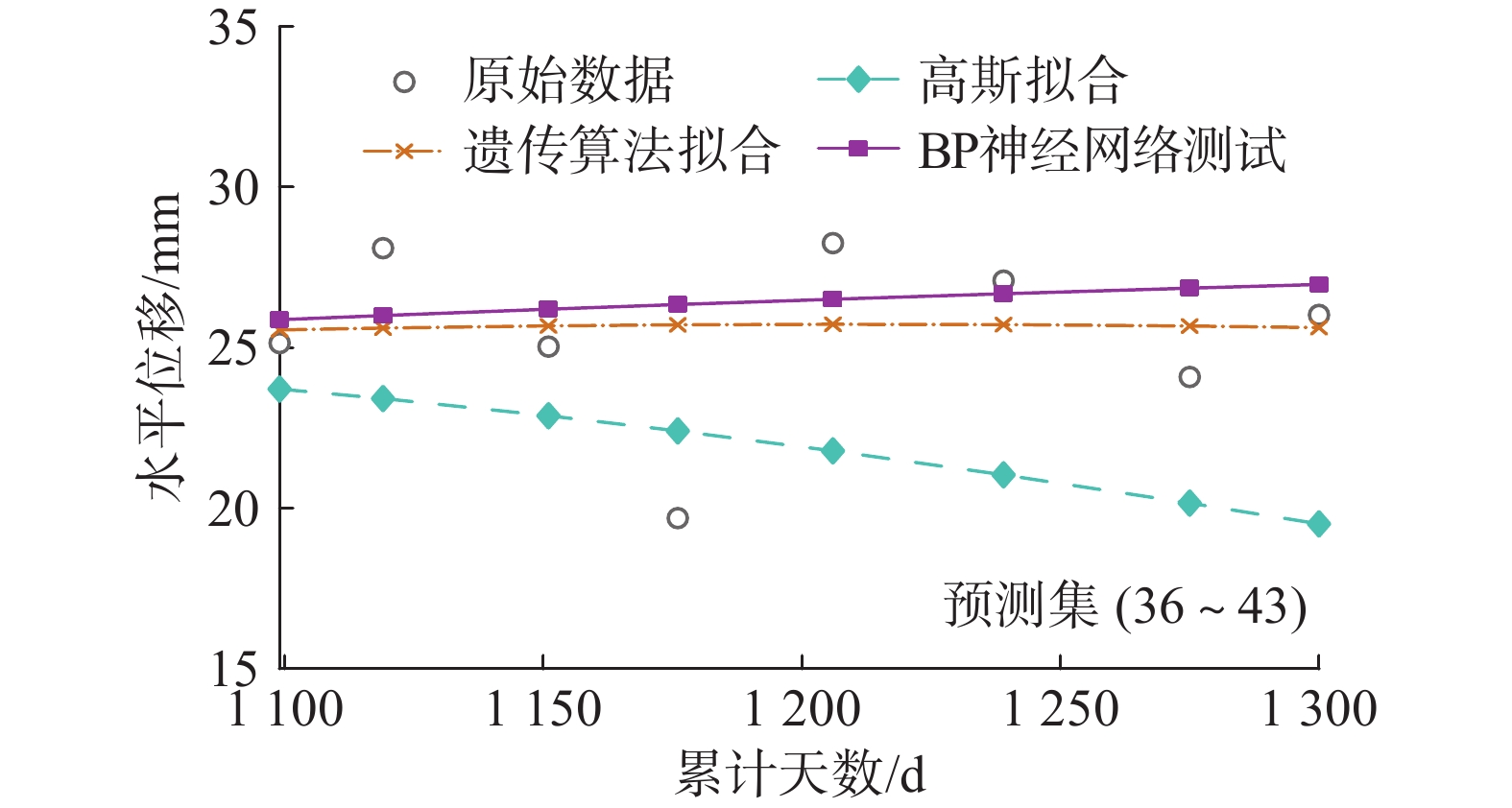
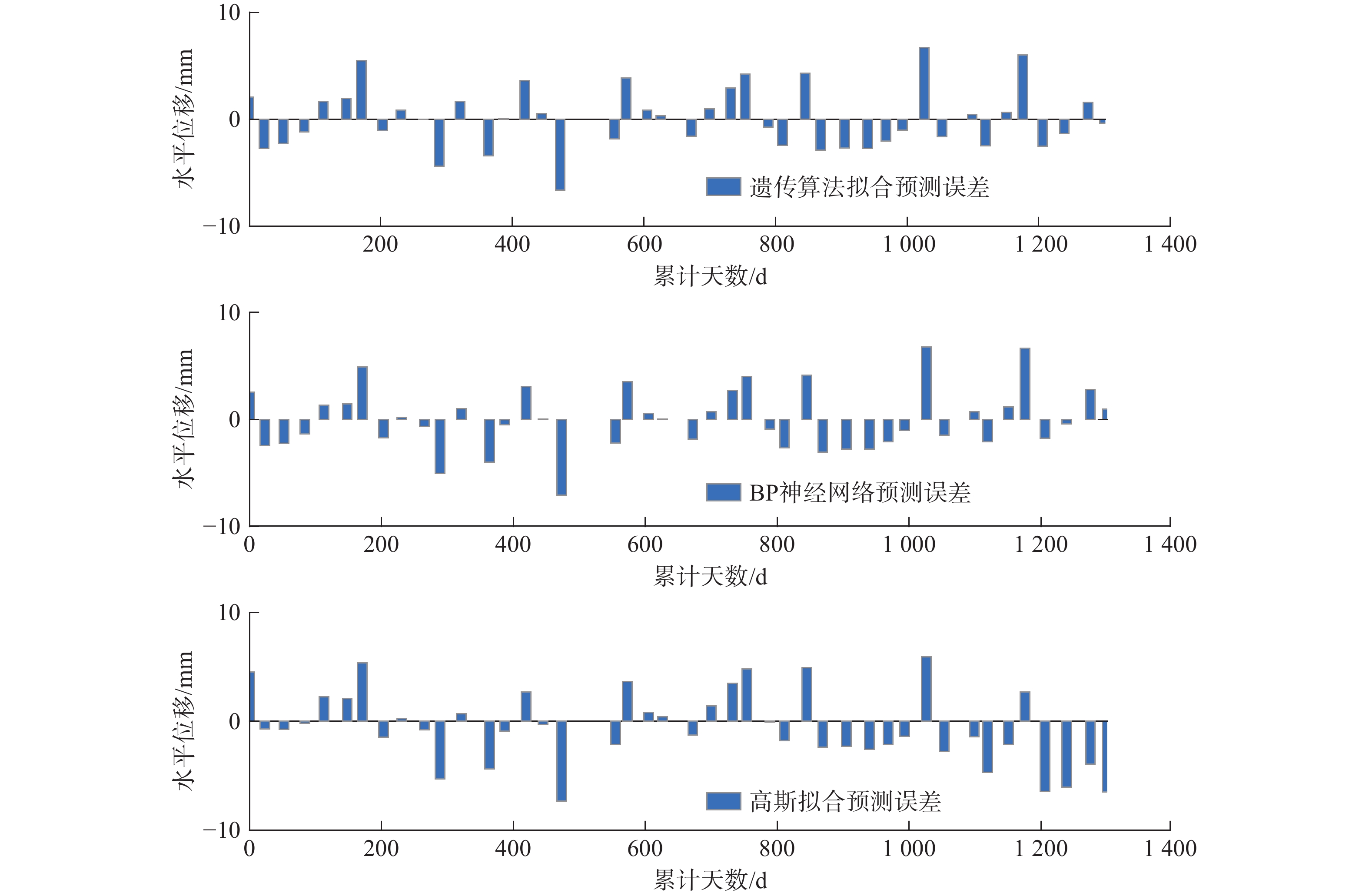
滑坡位移预测是预报滑坡灾害的重要依据，以往的滑坡位移预测模型多数为时间序列预测模型、BP神经网络预测模型、Gaussian拟合预测模型以及其他一些非线性预测模型。这些滑坡位移预测模型在建立上缺乏力学理论支撑，对不同力学特性产生的滑坡位移预测分析上没有针对性。文章针对力学特性为重力蠕变型滑坡位移的预测，提出一种基于遗传优化算法的滑坡蠕滑位移非线性预测模型。以鲁家坡滑坡东侧J05监测点的累计水平位移为例，划定测试区域与预测区域进行模型预测分析，并将新模型预测结果与Gaussian拟合预测模型、BP神经网络预测模型预测结果进行对比分析。结果表明，相较于传统预测模型，新模型的预测效果有所提升，有一定的工程价值与实践价值。
Abstract:Landslide displacement prediction is an important basis of predicting landslide disasters. Most of the previous landslide displacement prediction models include time series prediction models, BP neural network prediction models, Gaussian fitting prediction models, and various other nonlinear prediction models. However, these landslide displacement prediction models lack the foundation of mechanical theory in the establishment and have no pertinence in the prediction and analysis of landslide displacement resulting from diverse mechanical properties. In this paper, a nonlinear prediction model of landslide creep displacement based on genetic optimization algorithm is proposed for the prediction of gravity creep landslide displacement. Using the cumulative horizontal displacement data from monitoring point J05 on the eastern side of the Lujiapo landslide as a case study, the test area and prediction area are delimited for model prediction analysis. The results of the new model are compared with those of Gaussian fitting model and BP neural network model. The results indicate that, in comparison to the traditional prediction models, the new model exhibits improved predictive performance, offering a certain engineering value and practical value.
-
Keywords:
- landslide /
- displacement prediction /
- genetic algorithm /
- creep displacement /
- function model
-
0. 引言
中国是地质灾害高发国家之一，各类地质灾害给人们的生命和财产造成了巨大的损失[1]。滑坡灾害作为我国山区最具破坏力的地质灾害之一，对人民生活造成了重大影响。滑坡位移预测一直是众多学者研究防治滑坡灾害的重要依据，针对不同力学特性下的滑坡位移，选取相应的预测模型可以使得滑坡位移预测精度更高，效果更好。
近年来，随着各种机器学习算法与拟合理论的不断发展。对于滑坡位移的预测，曹博等[2]提出了一种蚁群算法优化极限学习机（extreme learning machine, ELM）滑坡位移预测模型；陈嘉伟[3]提出了一种粒子群算法优化BP神经网络滑坡位移预测模型（particle swarm optimization back propagation，PSO-BP）；王江荣[4]提出了用MATLAB工具箱进行的高斯拟合滑坡位移预测模型；杨伟东等[5]提出了一种结合自适应粒子群算法（adaptive particle swarm optimization, APSO）、支持向量机回归算法（support vector regression, SVR）、门控神经网络算法 （gated recurrent unit, GRU） 的组合模型。袁于思等[6]提出了粒子群算法优化改进支持向量机滑坡位移预测模型（PSO-DSRVM）等等。虽然这些模型预测精度较好，但在建立上仅有数学性，缺乏相关力学理论支撑，对不同力学特性产生的滑坡位移预测分析上没有针对性；同时，过分强调滑坡位移预测的精确性，可能会导致预测分析时将监测误差也考虑在预测范围内的情况发生，这使得滑坡预测模型产生了一定的过拟合性。
鉴于此，本文针对力学特性为重力蠕变型滑坡位移的预测，提出一种基于遗传优化算法的滑坡蠕滑位移非线性预测模型。以湖北省宜昌市兴山县鲁家坡滑坡J05监测点累计水平位移数据为例进行拟合预测分析，并将预测结果与一阶高斯拟合预测模型、BP神经网络预测模型预测结果做对比分析，证明本文预测模型的正确性与适用性。
考虑到目前滑坡位移时间序列预测方法在趋势项位移的分解上缺乏力学理论性与合理性。新型滑坡位移预测模型对滑坡位移时序趋势项分解也有一定的价值与借鉴意义。
1. 遗传算法模型
1.1 遗传算法简介
遗传算法（genetic algorithm，GA）是一种基于自然选择机理的全局优化求解方法[7]。遗传算法可以直接进行搜寻求解计算，没有求导或连续性的界定，其运算的随机搜索性使得其具有良好的全局寻优能力[8]。遗传算法解决问题的基本流程见图1。
1.2 遗传算法优化原理
滑坡位移非线性预测模型以拟合回归的统一决定系数RNL为优化目标，首先介绍拟合回归的最小二乘原理，如下：
滑坡位移拟合函数的通式为：
$$ \Delta \hat F = f(x)_{[a_0,a_1, \cdots ,a_{n - 1}]} $$ (1) 式中：
$ \Delta \hat F $ ——滑坡累计位移拟合值；x——时间变量；
$ [a_0,a_1, \cdots ,a_{n - 1}] $ ——函数内的最小二乘确定参数。按一定的时间周期监测所得的n个滑坡位移数据：
$$ (x_i,\Delta F_i),i=0,1,\cdots ,n-1 $$ (2) 式中：
$ \Delta F_i $ ——滑坡位移真值；$ x_i $ ——当期监测时间。将n个滑坡位移数据代入（1）式有：
$$ \Delta \hat F_i = f(x_i)_{[a_0,a_1, \cdots ,a_{n - 1}]} $$ (3) 为了使得拟合效果达到最好，需满足最小二乘函数F：
$$ F=\mathrm{min}{[(\Delta \hat{F}_i-\Delta F_i)}^{2}] $$ (4) 在（2）式中，
$ x_i $ 与$ \Delta F_i $ 已经给定。当拟合函数达到极值，即F对最小二乘确定参数偏导求解为0时，满足（4）式。滑坡位移拟合函数为非线性拟合函数，因此，满足（4）式需求解n个非线性方程组。采用Newton迭代法[9]，具体求解原理如下：对于
$ n $ 元非线性方程组，令：$$ f(a_k) = {[f_0(a_k),f_1(a_k) ,\cdots ,f_{n - 1}(a_k)]^{{T}}} $$ $$ a_k = [a_0,a_1 ,\cdots ,a_{n - 1}] $$ (5) 易得：
$$ \left\{ \begin{gathered} f_0(a_k) = \frac{{{\text{δ}} F}}{{{\text{δ}} a_0}} \\ f_1(a_k) = \frac{{{\text{δ}} F}}{{{\text{δ}} a_1}} \\ \quad\quad\vdots \\ f_{n - 1}(a_k) = \frac{{{\text{δ}} F}}{{{\text{δ}} a_{n - 1}}} \\ \end{gathered} \right. $$ (6) 构造Jacobi矩阵，如下：
$$ f'(a_k) = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{\text{δ}} f_0(a_k)}}{{{\text{δ}} a_0}}}&{\dfrac{{{\text{δ}} f_0(a_k)}}{{{\text{δ}} a_1}}}& \cdots &{\dfrac{{{\text{δ}} f_0(a_k)}}{{{\text{δ}} a_{n - 1}}}} \\ {\dfrac{{{\text{δ}} f_1(a_k)}}{{{\text{δ}} a_0}}}&{\dfrac{{{\text{δ}} f_1(a_k)}}{{{\text{δ}} a_1}}}& \cdots &{\dfrac{{{\text{δ}} f_1(a_k)}}{{{\text{δ}} a_{n - 1}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {\dfrac{{{\text{δ}} f_{n - 1}(a_k)}}{{{\text{δ}} a_0}}}&{\dfrac{{{\text{δ}} f_{n - 1}(a_k)}}{{{\text{δ}} a_1}}}& \cdots &{\dfrac{{{\text{δ}} f_{n - 1}(a_k)}}{{{\text{δ}} a_{n - 1}}}} \end{array}} \right] $$ (7) 在近似解
$ a_{k[j]} $ 处，将$ f(a_{k[j]}) $ 进行泰勒级数展开，略去二阶以上的高阶微量，易得：$$ f(a_k) \approx f(a_{k[j]}) + f'(a_{k[j]})(a_{k[j]} - a_k[j - 1]) $$ (8) 考虑到F对最小二乘确定参数偏导求解为0，有
$ f(a_k) = 0 $ ，得到近似方程，如下：$$ f(a_{k[j]}) + f'(a_{k[j]})(a_{k[j]} - a_{k[j - 1]})\approx 0 $$ (9) 令
$ \Delta a_k = a_{k[j]} - a_{k[j - 1]} $ ，那么Newton迭代式可写为：$$ \left\{ {\begin{split} &{a_{k[j]} = a_k[j - 1] + \Delta a_k} \\ &{f'(a_{k[j]})(\Delta a_k) + f(a_{k[j]}) \approx 0} \end{split}} \right. $$ (10) 令待求解参数Newton迭代初值为
$ a_{k[0]} $ ，设定迭代间距$ \Delta a_k $ ，在初值$ a_{k[0]} $ 处有：$$ \left[ {\begin{array}{*{20}{c}} {\dfrac{{{\text{δ}} f_0(a_{k[0]})}}{{{\text{δ}} a_0}}}&{\dfrac{{{\text{δ}} f_0(a_{k[0]})}}{{{\text{δ}} a_1}}}& \cdots &{\dfrac{{{\text{δ}} f_0(a_{k[0]})}}{{{\text{δ}} a_{n - 1}}}} \\ {\dfrac{{{\text{δ}} f_1(a_{k[0]})}}{{{\text{δ}} a_0}}}&{\dfrac{{{\text{δ}} f_1(a_{k[0]})}}{{{\text{δ}} a_1}}}& \cdots &{\dfrac{{{\text{δ}} f_1(a_{k[0]})}}{{{\text{δ}} a_{n - 1}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {\dfrac{{{\text{δ}} f_{n - 1}(a_{k[0]})}}{{{\text{δ}} a_0}}}&{\dfrac{{{\text{δ}} f_{n - 1}(a_{k[0]})}}{{{\text{δ}} a_1}}}& \cdots &{\dfrac{{{\text{δ}} f_{n - 1}(a_{k[0]})}}{{{\text{δ}} a_{n - 1}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta a_k} \\ {\Delta a_k} \\ \vdots \\ {\Delta a_k} \end{array}} \right] + $$ $$ \left[ {\begin{array}{*{20}{c}} {f_0(a_{k[0]})} \\ {f_1(a_{k[0]})} \\ \vdots \\ {f_{n - 1}(a_{k[0]})} \end{array}} \right] = {\boldsymbol{e}}_1 $$ (11) 开始迭代后，随着迭代间距
$ \Delta a_k $ 的累积，在$ a_{k[j]} $ 处有：$$ \left[ {\begin{array}{*{20}{c}} {\dfrac{{{\text{δ}} f_0(a_{k[j]})}}{{{\text{δ}} a_0}}}&{\dfrac{{{\text{δ}} f_0(a_{k[j]})}}{{{\text{δ}} a_1}}}& \cdots &{\dfrac{{{\text{δ}} f_0(a_{k[j]})}}{{{\text{δ}} a_{n - 1}}}} \\ {\dfrac{{{\text{δ}} f_1(a_{k[j]})}}{{{\text{δ}} a_0}}}&{\dfrac{{{\text{δ}} f_1(a_{k[j]})}}{{{\text{δ}} a_1}}}& \cdots &{\dfrac{{{\text{δ}} f_1(a_{k[j]})}}{{{\text{δ}} a_{n - 1}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {\dfrac{{{\text{δ}} f_{n - 1}(a_{k[j]})}}{{{\text{δ}} a_0}}}&{\dfrac{{{\text{δ}} f_{n - 1}(a_{k[j]})}}{{{\text{δ}} a_1}}}& \cdots &{\dfrac{{{\text{δ}} f_{n - 1}(a_{k[j]})}}{{{\text{δ}} a_{n - 1}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta a_k} \\ {\Delta a_k} \\ \vdots \\ {\Delta a_k} \end{array}} \right] + $$ $$ \left[ {\begin{array}{*{20}{c}} {f_0(a_{k[j]})} \\ {f_1(a_{k[j]})} \\ \vdots \\ {f_{n - 1}(a_{k[j]})} \end{array}} \right] = {\boldsymbol{e}}_j $$ (12) 当近似解
$ a_{k[j]} $ 处的误差$ {\boldsymbol{e}}_j $ 在指定的误差收敛区间$ (e_1,e_u) $ 内时，$ a_{k[j]} $ 即为所求滑坡位移拟合函数的参数精确解。相对于线性回归的决定系数
$ {R^2} $ ，引入测量学相对误差的概念，定义非线性回归方程的统一决定系数$ R_{\rm{NL}} $ [10]为：$$ R_{\rm{NL}} = 1 - \sqrt {\frac{{sse}}{{ssi}}} = 1 - \sqrt {\frac{{\displaystyle\sum\limits_{i = 0}^n {{{(\Delta \hat F_i - \Delta F_i)}^2}} }}{{\displaystyle\sum\limits_{i = 0}^n {{{(\Delta F_i)}^2}} }}} $$ (13) 式中：sse——残差平方和；
ssi——原值平方和。
$ R_{\rm{NL}} $ 表征的几何意义为拟合值与真值的相对距离误差比值。以
$ R_{\rm{NL}} $ 为拟合优度的评价标准，运用精度转换函数对参数初值$ a_{k[0]} $ 进行规定范围内取值，通过不断的遗传算法迭代找到$ R_{\rm{NL}} $ 最优值，即为本文的遗传算法优化原理。1.3 建立遗传算法模型
1.3.1 设定遗传算法迭代参数
根据遗传算法原理，设定遗传算法迭代参数。迭代参数的设定情况见表1。
表 1 遗传算法迭代参数Table 1. Iteration parameter of genetic algorithm参数名称 符号 种群数量 npop 迭代次数 maxit 染色体数 nv 交叉概率 npc 变异概率 nmu 子代数量 nc 表1中，种群数量、迭代次数、交叉概率、变异概率以及子代数量通过监测数据特征、迭代复杂度等因素综合确定。染色体数又为二进制变量个数，其具体确定方式如下：
设待求解参数初值
$ a_{k[0]} $ 的取值范围为$ [p,q] $ ，精度为$ {10^n} $ ，则$ a_{k[0]} $ 的取值个数为：$$ (q - p)\times {10^n} $$ (14) 根据求解得到的
$ a_{k[0]} $ 取值个数，对二进制变量个数进行确定，有如下关系式：$$ {2^{nv - 1}} \leqslant (q - p)\times {10^n} \leqslant {2^{nv}} $$ (15) 根据（15）式，求解nv的值，即可确定种群个体染色体数。
1.3.2 建立种群适应度函数
迭代参数设定完成后，根据遗传算法求解流程，建立种群适应度函数。
首先建立
$ a_{k[0]} $ 的精度转换函数，精度转换公式如下：$$ a_{k[0]} = p + I_D\frac{{(q - p)}}{{{2^{nv}} - 1}} $$ (16) 式中：ID——种群个体十进制数。
根据转换后的待求解参数初值
$ a_{k[0]} $ ，以RNL为种群的基准适应度，建立最小二乘适应度函数。适应度函数程序设计技术路线，如图2。1.3.3 建立遗传算法主函数
确定相关参数与适应度函数后，建立遗传算法主函数。
建立自然进化模型，自然进化包含有选择、交叉、变异、重组四个过程。
考虑到问题搜索效率与难易程度，选择阶段设定模型为轮盘赌选择模型；并改进适应度函数为：
$$ fitness = \left\{ \begin{gathered} 1 - 0.5 \times {\left(\left| {\frac{{f - b}}{a}} \right|\right)^\alpha },\; \;\;\left| {f - b} \right| < a \\ \frac{1}{{1 + {{\left| {\dfrac{{f - b}}{a}} \right|}^\beta }}},\;\;\quad\quad\quad\left| {f - b} \right| \geqslant a \\ \end{gathered} \right. $$ (17) 式中：fitness——改进后的适应度；
f——原适应度；
a、b、β——改进调整参数。
根据优化经验，β取2，α取1，b取当代最优目标值fmax，且有a定义如下：
$$ a = \max \left[0.5,\frac{{\left| {\max (f - {f_{\max }})} \right|}}{{30}}\right] $$ (18) 交叉与变异阶段选择合适的交叉算子npc与变异算子nmu进行交叉与变异。
重组阶段下，将交叉与变异处理后的个体同父代组合起来，计算适应度。根据适应度大小择优选取npop个个体，组成父代，重新进入选择阶段。
建立自然进化模型后，设置转接矩阵和接收矩阵进行数据转接与接收结果。完成所有操作后，建立循环进行遗传算法迭代。
2. 蠕滑位移预测
2.1 实例简介
鲁家坡滑坡位于湖北省宜昌市兴山县。滑坡主滑方向为317°，滑坡体纵长约330 m，前缘宽约170 m，后缘宽约65 m，平均宽度85 m。分布面积约2.7×104 m2，滑坡平均厚度8 m，滑坡体积约29.6×104 m3。坡体物质组成主要为粉质黏土、含碎石粉质黏土、含砾粉质黏土、碎石土等。地层岩性为中侏罗统泄滩组（J2x）泥质粉砂岩，岩层总体产状240°～266°∠38°～48°。鲁家坡滑坡全貌见图3。
2010年，鲁家坡坡体在经历地表变形裂缝、房屋倒塌、局部坍塌等重大地质灾害后，湖北省地质局针对地质灾害严重程度于2012年对鲁家坡坡体进行了综合治理。综合治理之后，短时间内，鲁家坡坡体基本保持稳定。现今，鲁家坡坡体部分区域出现较大滑坡位移变形，综合考虑鲁家坡坡体稳定性情况，建立监测系统进行监测预报。
监测项目于2018年8月建立，内部设有5个监测点（J01—J05），2018年9月开始进行项目监测，2022年9月完成项目监测。考虑到鲁家坡滑坡东侧发生过较为严重的变形破坏，选取滑坡东侧J05监测点2018年9月至今累计水平位移数据为本次拟合模型的计算数据。
2.2 建模计算
鲁家坡坡体为似均匀土质边坡体，据著作[11]，滑坡变形破坏力学机制模式的形成条件得出结论，坡体主要发生重力蠕变型破坏，其产生的滑坡位移可作为蠕滑位移进行研究。
蠕滑位移的变形阶段主要分为衰减蠕变、等速蠕变和加速蠕变三个阶段[12]，不同的坡体应力条件下，蠕滑位移的变化表现为不同形式。
当温度、气压、降水量等因素在一定变化范围内时，根据坡体应力
$ \sigma $ 与岩土体屈服强度下限$ \sigma_{{\mathrm{sl}}} $ 、屈服强度上限（长期强度）$ \sigma_{{\mathrm{su}}} $ 的不同大小关系，可得到三条不同应力条件下的应变-时间（$ \varepsilon \text- t $ ）曲线，见图4。（1）当
$ \sigma \leqslant \sigma_{{\mathrm{sl}}} $ 时，应变-时间关系表现为①曲线。表达方程通式为：$$ \varepsilon = A_1(1 - B_1{e^{ - C_1t}}) $$ (19) （2）当
$ \sigma_{{\mathrm{sl}}} \leqslant \sigma \leqslant \sigma_{{\mathrm{su}}} $ 时，应变-时间关系表现为②曲线。表达方程通式为：$$ \varepsilon = A_2(1 - B_2{e^{ - C_2t}}) + D_1t $$ (20) （3）当
$ \sigma >\sigma_{{\mathrm{su}}} $ 时，应变-时间关系表现为③曲线。表达方程通式为：$$ \varepsilon = A_3(1 - B_3{e^{ - C_3t}}) + P_1{t^3} + Q_1{t^2} + D_2t $$ (21) 式中，
$ A_1、A_2、A_3 $ 等字母参数是表征影响坡体蠕滑应变的地质力学常量。由相关弹塑性理论可知，监测点水平位移-时间变化曲线应与蠕变曲线保持一致。
根据2018年9月至今监测点水平位移数据，得到水平位移-时间散点图，见图5。
![]()
图 5 监测点水平位移-时间散点分布Figure 5. Scatter distribution of horizontal displacement vs. time at monitoring points据图5，监测点水平位移数据共43组。机器学习中常用测试数据、验证数据与预测数据的分布比例为（0.5, 0.25, 0.25）或（0.6, 0.2, 0.2）。考虑到水平位移蠕变拟合模型已经确定，不需要单独进行模型验证。因此，本文设定水平位移测试数据与预测数据分布比例为（0.8, 0.2）。即前35组为测试数据，后8组为预测验证数据。所得区域分布图见图6。
![]()
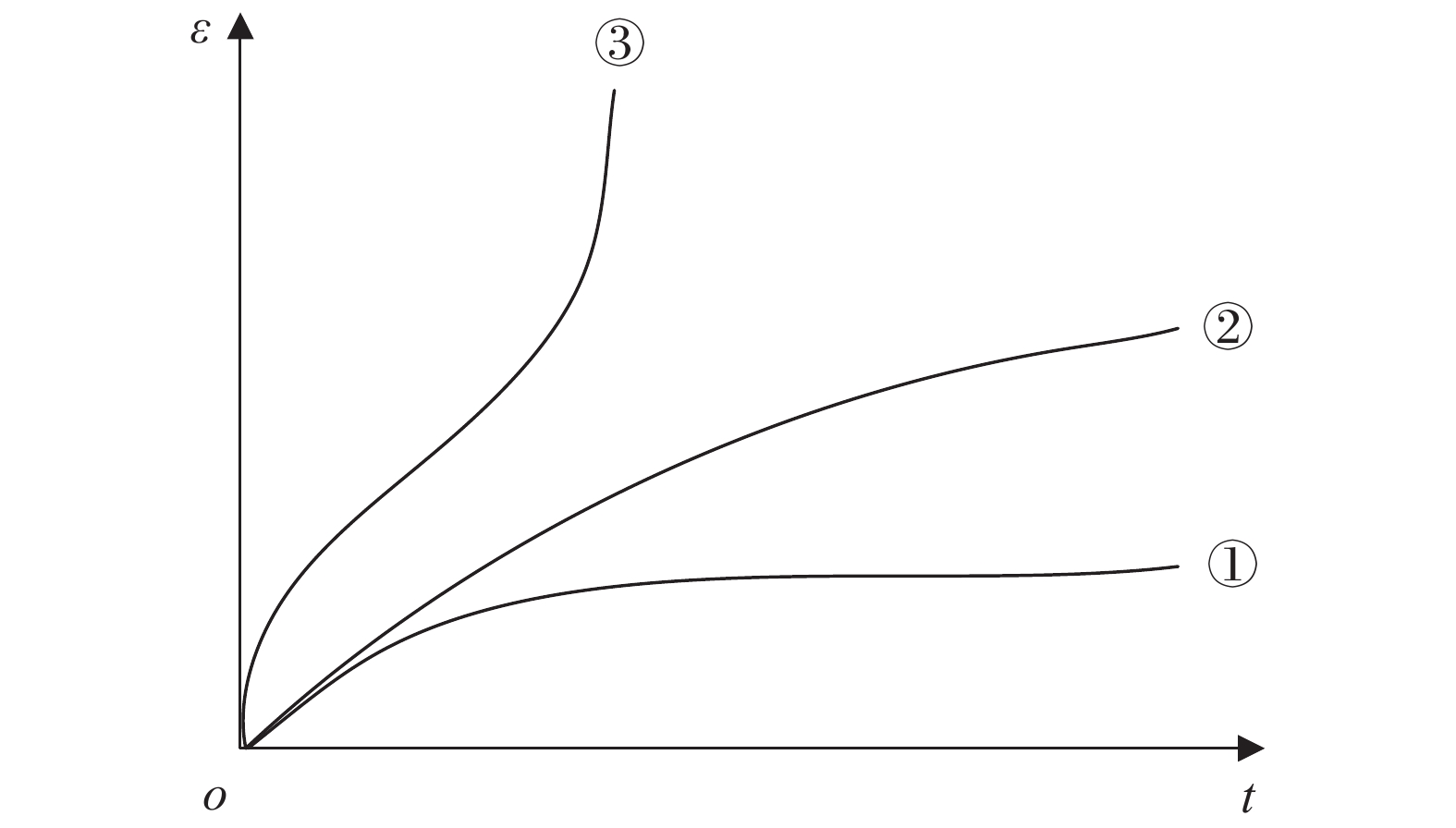
图 6 监测点水平位移-时间散点区域分布Figure 6. Scatter area distribution of horizontal displacement vs. time at monitoring points根据水平位移散点分布特征以及不同应力条件下的蠕变曲线图像特征选定拟合函数表达式为式（20），表现曲线为②曲线。考虑到计算的便捷度，对拟合函数表达式做一定的调整，如下：
$$ y(t) = \frac{{a_1}}{{1 - b_1{e^{{c_1}t}}}} + d_1t + D $$ (22) 根据函数的求解难度，对线型参数初值
$ a_{1[0]}、 b_{1[0]}、d_{1[0]}、D_{[0]} $ 进行大范围搜索取值，对指数型参数初值$ c_{1[0]} $ 取值范围进行约束。据前期经验调试，设定五个参数取值范围，如下：$$ \left[ \begin{gathered} {a_{1[0]}} \\ {b_{1[0]}} \\ {c_{1[0]}} \\ {d_{1[0]}} \\ D_{[0]} \\ \end{gathered} \right] = \left[ \begin{gathered} {[ - 50{\text{ }}000,100{\text{ }}000]} \\ {[ - 50{\text{ }}000,100{\text{ }}000]} \\ {[ - 100,100]} \\ {[ - 50{\text{ }}000,100{\text{ }}000]} \\ [ - 50{\text{ }}000,100{\text{ }}000] \\ \end{gathered} \right] $$ (23) 根据水平位移测试数据分布特征、迭代复杂度、迭代效率等因素设定遗传算法迭代参数，见表2。
表 2 遗传算法迭代参数设定表Table 2. Genetic algorithm iteration parameter configuration table迭代参数 数值 npop 30 maxit 500 nvar 23 npc 0.9 nmu 0.1 nc 27 将水平位移测试数据、遗传算法迭代参数、待求解参数初值取值范围以及拟合函数模型代入程序内，得到拟合优化结果。如下：
迭代完成后，以
$ R_{\rm{NL}} $ 变化点为进化分界点。得到测试数据统一决定系数迭代过程见图7。![]()
图 7 测试数据统一决定系数迭代过程Figure 7. Iteration process of determination for the test data iterative process设置初始种群适应度
$ R_{\rm{NL}} $ 最优值为进化零阶段，并使得随着迭代次数增加，每次$ R_{\rm{NL}} $ 变化后均进入下一个进化阶段，得到测试数据拟合模型迭代进化表，见表3。表 3 测试数据拟合模型迭代进化表Table 3. Iterative evolution table of test data fitting models进化阶段 迭代次数 统一决定系数RNL 0 1 0.828 0 1 101 0.839 6 2 106 0.839 8 3 151 0.840 6 4 221 0.845 0 据表3，算法种群分别进入了5个进化阶段。最优进化阶段的
$ R_{\rm{NL}} $ 为0.845 0。导出拟合模型各进化阶段求解参数表，见表4。表 4 拟合模型各进化阶段求解参数Table 4. Parameters solutions at each evolution stage of the fit model参数 a1 b1 c1 d1 D RNL 进化阶段 0 +388.3 −1.351×10−2 −3.786×101 +2.179×10−2 −383.2 0.828 0 1 +421.8 −1.937×10−1 −1.003×10−3 −1.770×10−2 −351.0 0.839 6 2 +454.2 −9.954×10−2 −1.257×10−3 −5.410×10−3 −411.1 0.839 8 3 +136.4 −8.182×10−1 −1.667×10−3 −2.010×10−2 −72.96 0.840 6 4 +6.379 −2.524×104 −4.264×10−2 +1.620×10−2 +3.167 0.845 0 根据各进化点求解参数值，得到进化点函数拟合曲线，见图8。
根据不同应力条件下的蠕变②曲线形状特征，剔除最优解，保留次优解，得到测试数据拟合函数方程，如下：
$$ y(t) = \frac{{136.4}}{{1 + 0.818{\text{ }}2{{\mathrm{e}}^{ - 0.001{\text{ }}667t}}}} - 0.020{\text{ }}10t - 72.96 $$ (24) 根据式（24）与测试数据散点分布，得到测试数据拟合结果图，如图9。
2.3 预测效果对比分析
滑坡位移预测分析常用的方法有广义线性函数拟合预测、非线性函数拟合预测、时间序列预测、BP神经网络预测等等。
根据预测模型原理不同，将遗传算法拟合预测模型与其表达式类似的Gaussian非线性拟合预测模型以及常用的BP（back propagation）神经网络预测模型做对比分析。
本次对比试验中，Gaussian拟合预测模型采用一阶Gaussian模型。其原理[14]为：
将水平位移测试数据
$ (t_i,y_i),(i=0,1\cdots ,n-1) $ 运用一阶Gaussian模型描述有：$$ {y_i} = {y_{\max }}\exp \left[ - \frac{{{{({t_i} - {t_{\max }})}^2}}}{S}\right] $$ (25) 式中，待估参数为ymax、tmax和S。代表的几何意义分别为高斯曲线的峰值、峰值位置和半宽度信息。
对式（25）两边取自然对数处理并进行化简，则有：
$$ \mathrm{ln}{y}_{i}=\left(\mathrm{ln}{y}_{\mathrm{max}}-\frac{{t}_{\mathrm{max}}{}^{2}}{S}\right)+\frac{2{t}_{i}{t}_{\mathrm{max}}}{S}-\frac{{t}_{i}{}^{2}}{S} $$ (26) 对式（26）进行广义最小二乘求解即可得到待估参数ymax、tmax和S。
应用一阶Gaussian模型对测试数据拟合后的表达式如下:
$$ y（t） = 24.81{{\mathrm{e}}^{ - \tfrac{{{{(t - 944.6)}^2}}}{{{{725.2}^2}}}}} $$ (27) 同时，对比试验中的BP神经网络预测模型原理如下：
BP 神经网络预测模型的原理是将时间变量以一定的权重与偏执传入输入层，然后经过神经网络隐含层各节点映射后得到输出层[15]。将输出数据与原始数据做对比，得到误差损失函数，如下：
$$ E = \frac{1}{2}{({y_k} - {y_i})^2} $$ (28) 式中：yk——输出数据；
yi——原始数据；
E——误差损失函数值。
通过误差损失函数对权重与偏执系数进行梯度下降修正，直到满足预测设置要求。
预测模型以Bayesian-regularization为训练方法，模型的训练集、验证集与测试集数据占比分别为0.7、0.15、0.15，预测神经元数量为15，预测范围随机。当测试数据训练至误差较小、数据曲线与蠕变模型曲线类似时，训练停止。
经计算，得到三种预测模型的测试数据拟合曲线，如图10。
将水平位移测试数据与预测数据分别代入遗传算法拟合预测模型、Gaussian拟合预测模型以及BP神经网络预测模型。得到三种模型的原始数据拟合曲线与预测数据拟合曲线如图11—12。
![]()
图 11 三种预测模型的原始数据拟合曲线Figure 11. Fitting curves of original data for three prediction models![]()
图 12 三种预测模型的预测数据拟合曲线Figure 12. Fitting curves of predicted data for three prediction models计算三种预测模型的绝对误差值，得到的三种预测模型的拟合绝对误差统计如图13。
![]()
图 13 三种预测模型绝对误差统计Figure 13. Statistical analysis of absolute errors for three prediction models据图13，三种模型拟合绝对误差均在误差控制区间（−10, 10）内，且经计算所得，三种预测模型的拟合优度指标RNL均在0.8以上，可认为三种预测模型的拟合效果较好。
在满足拟合优度与误差控制度的基础上，为了进一步对比遗传算法拟合预测模型、Gaussian拟合预测模型和BP神经网络预测模型的预测效果，计算三种预测模型预测区域内的统计学指标：均方根误差RMSE、统一决定系数RNL、角余弦系数FR以及线性原始决定系数R2，计算结果见表5。
表 5 三种预测模型预测区域统计学指标Table 5. Statistical metrics for prediction regions of three prediction models预测方法 遗传算法拟合预测 高斯拟合预测 BP神经网络预测 统计学
指标RNL 0.897 5 0.817 4 0.888 2 RMSE 2.596 7 4.639 1 2.790 4 FR 0.994 9 0.992 7 0.994 8 R2 0.991 2 −1.216 2 0.826 7 在三种预测模型拟合优度以及误差控制度均满足要求，无法对比预测效果的情况下，为了进一步评价三种模型的预测效果，需建立预测区域评价指标。
考虑到单项预测效果评价指标可能造成的预测效果评价不精确，评价效果差的情况。建立综合预测区域评价指标，如下：
在已有的综合预测模型评价方法[16 − 18]的基础上，根据计算所得的三种模型预测区域统计学指标，建立综合预测效果指数Kpi，确定方式如下：
$$ K_{pi} = \dfrac{{w_1\dfrac{{R_{{{\mathrm{NL}}}(i)}}}{{R_{{{\mathrm{NL}}}{{(M)}}}}} + w_2\dfrac{{RMS E_{(i)}}}{{RMS E_{{(M)}}}} + w_3\dfrac{{FR_{(i)}}}{{FR_{{(M)}}}} + w_4\dfrac{{R^2_{(i)}}}{{R^2_{{(M)}}}}}}{{\displaystyle\sum\limits_{n = 1}^4 {w_n} }} $$ (29) 式中：i=1, 2, 3，分别代表三种预测模型；wn表示各项参数表征预测效果权重值，正向影响参数权重取正，负向影响参数权重取负；（M）表示各项指标标准值，其中，相关系数类型取0.8，均方根误差取2.5，角余弦系数取1.0。
考虑到三种预测模型均为非线性预测模型，R2对非线性预测模型的预测效果表征性差，且FR为辅助验证RNL的几何表征参数[10]。则有，设定FR与R2为辅助型预测效果评价指标，RNL与RMSE为主导型预测效果评价指标。根据熵权法下的预测评价权重确定方法[16]，主辅预测效果评价指标权重偏置，权重选取经验以及各项统计学指标的预测表征程度，确定各项参数表征预测效果权重
$ w_1、w_2、w_3、w_4 $ 经验值，如下：$$ \left\{ \begin{split} & w_1 = 1.2 \\ & w_2 = - 0.8 \\ & w_3 = 0.6 \\ & w_4 = 0.6 \\ \end{split} \right. $$ (30) 经计算得到三种预测模型的综合预测效果指数如下：
$$ \left\{ \begin{split} &K_{p1} = 1.030{\text{ }}0 \\ &K_{p2} = - 0.591{\text{ }}3 \\ &K_{p3} = 0.896{\text{ }}6 \\ \end{split} \right. $$ (31) 遗传算法拟合预测模型、Gaussian拟合预测模型、BP神经网络预测模型的综合预测效果指数分别为：1.0300、−0.5913、0.8966。
综合预测效果指数是正向指数，根据计算结果可得，遗传算法拟合预测模型的预测效果最好。并且，遗传算法拟合预测模型相较Gaussian拟合预测模型与BP神经网络预测模型，预测效果分别提高了274.2%、14.9%。
综上所述，遗传算法拟合预测模型相较于其他两个预测模型，预测精度更高，误差更小，预测效果更好。但是，当应急处理滑坡监测水平位移数据量增多时，可能会陷入局部最优状况，无法得到全局最优的拟合结果。同时，由强降雨等其他极端天气使得滑坡产生阶跃位移时，优化所得预测结果并不准确。
3. 结语
本文结合遗传算法与西原蠕变模型，建立了一种新型的基于遗传算法优化情况下的滑坡蠕滑位移预测模型。以鲁家坡滑坡累计水平位移数据为例进行拟合预测分析，并将模型预测结果与一阶高斯拟合预测模型、BP神经网络预测模型预测结果做对比分析。分析结果表明，相较其他两种预测模型，新模型的预测效果有所提升。但是，当滑坡水平位移数据量增多时，可能会出现拟合结果局部最优的情况；且当滑坡遭遇极端天气以及地震等突发灾害致使滑坡产生阶跃位移时，预测结果不准确。因此，如何解决数据量增多时的局部最优问题与阶跃位移预测问题将是下一步的主要研究方向。
文中提出的新型预测模型应用案例仅有鲁家坡滑坡一例，模型是否可以广泛应用于重力蠕变型滑坡位移的预测还有待于更多实例验证。
-
![]()
图 5 监测点水平位移-时间散点分布
Figure 5. Scatter distribution of horizontal displacement vs. time at monitoring points
![]()
图 6 监测点水平位移-时间散点区域分布
Figure 6. Scatter area distribution of horizontal displacement vs. time at monitoring points
![]()
图 7 测试数据统一决定系数迭代过程
Figure 7. Iteration process of determination for the test data iterative process
![]()
图 11 三种预测模型的原始数据拟合曲线
Figure 11. Fitting curves of original data for three prediction models
![]()
图 12 三种预测模型的预测数据拟合曲线
Figure 12. Fitting curves of predicted data for three prediction models
![]()
图 13 三种预测模型绝对误差统计
Figure 13. Statistical analysis of absolute errors for three prediction models
表 1 遗传算法迭代参数
Table 1 Iteration parameter of genetic algorithm
参数名称 符号 种群数量 npop 迭代次数 maxit 染色体数 nv 交叉概率 npc 变异概率 nmu 子代数量 nc 
下载: 导出CSV
表 2 遗传算法迭代参数设定表
Table 2 Genetic algorithm iteration parameter configuration table
迭代参数 数值 npop 30 maxit 500 nvar 23 npc 0.9 nmu 0.1 nc 27
下载: 导出CSV
表 3 测试数据拟合模型迭代进化表
Table 3 Iterative evolution table of test data fitting models
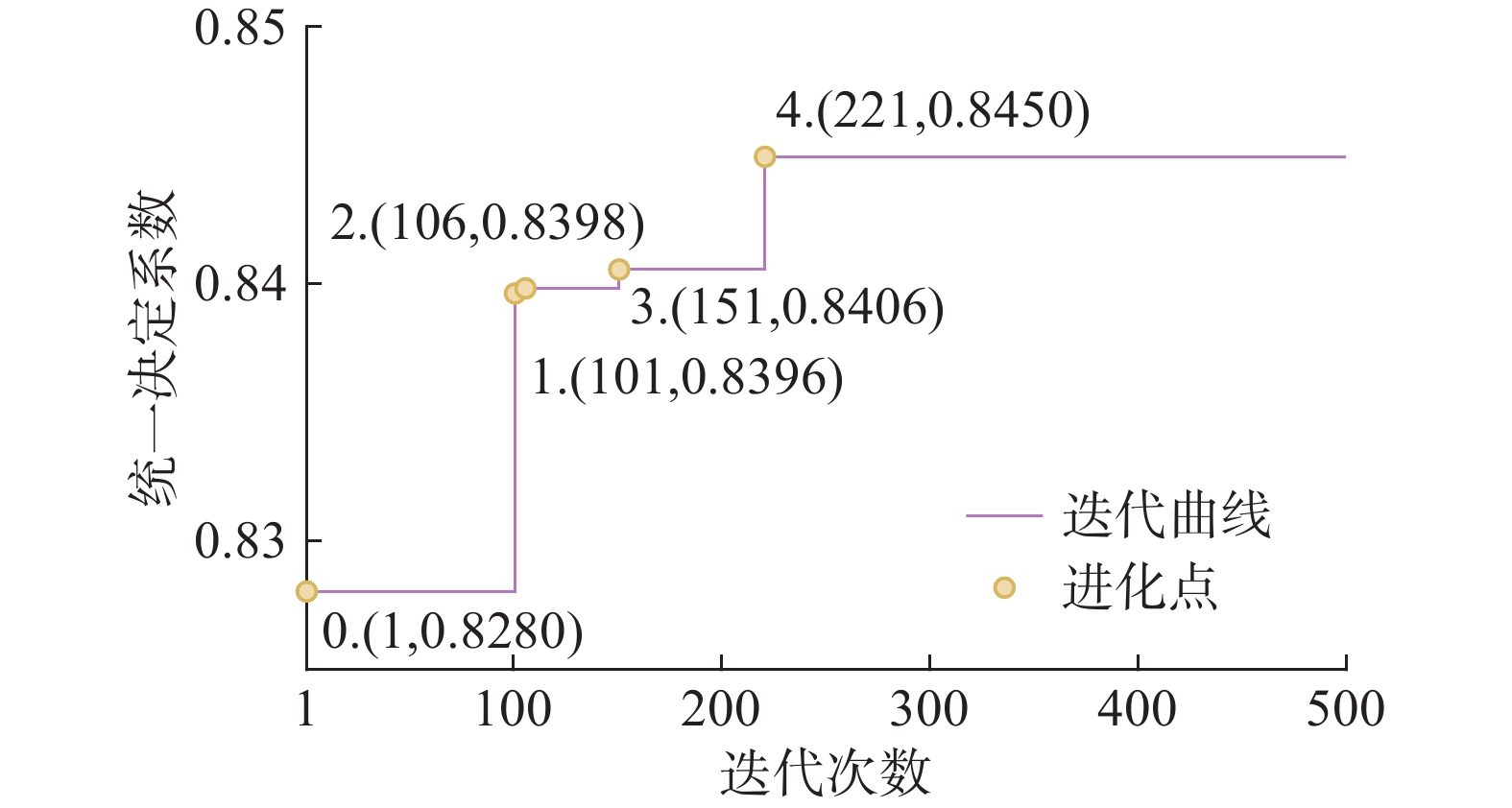
进化阶段 迭代次数 统一决定系数RNL 0 1 0.828 0 1 101 0.839 6 2 106 0.839 8 3 151 0.840 6 4 221 0.845 0
下载: 导出CSV
表 4 拟合模型各进化阶段求解参数
Table 4 Parameters solutions at each evolution stage of the fit model
参数 a1 b1 c1 d1 D RNL 进化阶段 0 +388.3 −1.351×10−2 −3.786×101 +2.179×10−2 −383.2 0.828 0 1 +421.8 −1.937×10−1 −1.003×10−3 −1.770×10−2 −351.0 0.839 6 2 +454.2 −9.954×10−2 −1.257×10−3 −5.410×10−3 −411.1 0.839 8 3 +136.4 −8.182×10−1 −1.667×10−3 −2.010×10−2 −72.96 0.840 6 4 +6.379 −2.524×104 −4.264×10−2 +1.620×10−2 +3.167 0.845 0
下载: 导出CSV
表 5 三种预测模型预测区域统计学指标
Table 5 Statistical metrics for prediction regions of three prediction models
预测方法 遗传算法拟合预测 高斯拟合预测 BP神经网络预测 统计学
指标RNL 0.897 5 0.817 4 0.888 2 RMSE 2.596 7 4.639 1 2.790 4 FR 0.994 9 0.992 7 0.994 8 R2 0.991 2 −1.216 2 0.826 7
下载: 导出CSV
-
[1] 吴明辕,罗明,刘岁海. 基于光学遥感与InSAR技术的潜在滑坡与老滑坡综合识别——以滇西北地区为例[J]. 中国地质灾害与防治学报,2022,33(3):84 − 93. [WU Mingyuan,LUO Ming,LIU Suihai. Comprehensive identification of potential and old landslides based on optical remote sensing and InSAR technologies:A case study in northwestern Yunnan Province[J]. The Chinese Journal of Geological Hazard and Control,2022,33(3):84 − 93. (in Chinese with English abstract)] WU Mingyuan, LUO Ming, LIU Suihai . Comprehensive identification of potential and old landslides based on optical remote sensing and InSAR technologies: A case study in northwestern Yunnan Province［J］. The Chinese Journal of Geological Hazard and Control,2022 ,33 （3 ）:84 −93 . （in Chinese with English abstract）[2] 曹博,汪帅,宋丹青,等. 基于蚁群算法优化极限学习机模型的滑坡位移预测[J]. 水资源与水工程学报,2022,33(2):172 − 178. [CAO Bo,WANG Shuai,SONG Danqing,et al. Landslide displacement prediction based on extreme learning machine optimized by ant colony algorithm[J]. Journal of Water Resources and Water Engineering,2022,33(2):172 − 178. (in Chinese with English abstract)] CAO Bo, WANG Shuai, SONG Danqing, et al . Landslide displacement prediction based on extreme learning machine optimized by ant colony algorithm［J］. Journal of Water Resources and Water Engineering,2022 ,33 （2 ）:172 −178 . （in Chinese with English abstract）[3] 陈嘉伟. 基于ARIMA模型与PSO-BP神经网络算法的滑坡位移预测及研究[D]. 宜昌:三峡大学,2020. [CHEN Jiawei. Displacement forecast and research based on ARIMA model and PSO-BP neural network[D]. Yichang:China Three Gorges University,2020. (in Chinese with English abstract)] CHEN Jiawei. Displacement forecast and research based on ARIMA model and PSO-BP neural network[D]. Yichang: China Three Gorges University, 2020. （in Chinese with English abstract）
[4] 王江荣. 高斯函数模型在变形监测数据处理中的应用[J]. 金属矿山,2015(4):178 − 181. [WANG Jiangrong. Application of the Gauss function model in data processing of deformation monitoring[J]. Metal Mine,2015(4):178 − 181. (in Chinese with English abstract)] WANG Jiangrong . Application of the Gauss function model in data processing of deformation monitoring［J］. Metal Mine,2015 （4 ）:178 −181 . （in Chinese with English abstract）[5] 杨伟东,王再旺,赵涵卓,等. 基于APSO-SVR-GRU模型的白水河滑坡周期项位移预测[J]. 中国地质灾害与防治学报,2022,33(6):20 − 28. [YANG Weidong,WANG Zaiwang,ZHAO Hanzhuo,et al. Displacement prediction of periodic term of Baishuihe landslide based on APSO-SVR-GRU model[J]. The Chinese Journal of Geological Hazard and Control,2022,33(6):20 − 28. (in Chinese with English abstract)] YANG Weidong, WANG Zaiwang, ZHAO Hanzhuo, et al . Displacement prediction of periodic term of Baishuihe landslide based on APSO-SVR-GRU model［J］. The Chinese Journal of Geological Hazard and Control,2022 ,33 （6 ）:20 −28 . （in Chinese with English abstract）[6] 袁于思,冯小鹏,李勇,等. 基于PSO-DSRVM的边坡变形预测[J]. 中国地质灾害与防治学报,2023,34(1):1 − 7. [YUAN Yusi,FENG Xiaopeng,LI Yong,et al. Prediction of mine slope deformation based on PSO-DSRVM[J]. The Chinese Journal of Geological Hazard and Control,2023,34(1):1 − 7. (in Chinese with English abstract)] YUAN Yusi, FENG Xiaopeng, LI Yong, et al . Prediction of mine slope deformation based on PSO-DSRVM［J］. The Chinese Journal of Geological Hazard and Control,2023 ,34 （1 ）:1 −7 . （in Chinese with English abstract）[7] 胡鹏,文章,胡新丽,等. 基于遗传算法-支持向量机的滑坡渗透系数反演[J]. 水文地质工程地质,2021,48(4):160 − 168. [HU Peng,WEN Zhang,HU Xinli,et al. Estimation of hydraulic conductivity of landslides based on support vector machine method optimized with genetic algorithm[J]. Hydrogeology & Engineering Geology,2021,48(4):160 − 168. (in Chinese with English abstract)] HU Peng, WEN Zhang, HU Xinli, et al . Estimation of hydraulic conductivity of landslides based on support vector machine method optimized with genetic algorithm［J］. Hydrogeology & Engineering Geology,2021 ,48 （4 ）:160 −168 . （in Chinese with English abstract）[8] 张艳,宦飞. 一种应用遗传算法的彩色图像分割方法[J]. 计算机应用与软件,2011,28(3):237 − 239. [ZHANG Yan,HUAN Fei. A colour image segmentation method using genetic algorithm[J]. Computer Applications and Software,2011,28(3):237 − 239. (in Chinese with English abstract)] ZHANG Yan, HUAN Fei . A colour image segmentation method using genetic algorithm［J］. Computer Applications and Software,2011 ,28 （3 ）:237 −239 . （in Chinese with English abstract）[9] 王晓峰,石东伟. 数值分析[M]. 郑州:河南大学出版社,2019. [WANG Xiaofeng,SHI Dongwei. Numerical analysis[M]. Zhengzhou,China:Henan University Press,2019. (in Chinese)] WANG Xiaofeng, SHI Dongwei. Numerical analysis[M]. Zhengzhou, China: Henan University Press, 2019. （in Chinese）
[10] 张世强. 曲线回归的拟合优度指标的探讨[J]. 中国卫生统计,2002,19(1):9 − 11. [ZHANG Shiqiang. Approach on the fitting optimization index of curve regression[J]. Chinese Journal of Health Statistics,2002,19(1):9 − 11. (in Chinese with English abstract)] ZHANG Shiqiang . Approach on the fitting optimization index of curve regression［J］. Chinese Journal of Health Statistics,2002 ,19 （1 ）:9 −11 . （in Chinese with English abstract）[11] 张倬元,王士天,王兰生. 工程地质分析原理[M]. 4版. 北京:地质出版社,2016. [ZHANG Zhuoyuan,WANG Shitian,WANG Lansheng. Principles of engineering geological analysis[M]. 4th ed. Beijing:Geological Publishing House,2016. (in Chinese)] ZHANG Zhuoyuan, WANG Shitian, WANG Lansheng. Principles of engineering geological analysis[M]. 4th ed. Beijing: Geological Publishing House, 2016. （in Chinese）
[12] 许强,汤明高,黄润秋,等. 大型滑坡监测预警与应急处置[M]. 北京:科学出版社,2015. [XU Qiang,TANG Minggao,HUANG Runqiu,et al. Monitoring,early warning and emergency disposal of large landslide[M]. Beijing:Science Press,2015. (in Chinese)] XU Qiang, TANG Minggao, HUANG Runqiu, et al. Monitoring, early warning and emergency disposal of large landslide[M]. Beijing: Science Press, 2015. （in Chinese）
[13] 陈浩,杨春和,任伟中. 蠕动滑坡变形机制的理论分析与模型试验研究[J]. 岩石力学与工程学报,2008,27(增刊2):3705 − 3711. [CHEN Hao,YANG Chunhe,REN Weizhong. Theoretical analysis and model test study on deformation mechanism of creep landslide[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(Sup 2):3705 − 3711. (in Chinese with English abstract)] CHEN Hao, YANG Chunhe, REN Weizhong. Theoretical analysis and model test study on deformation mechanism of creep landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27（Sup 2）: 3705 − 3711. （in Chinese with English abstract）
[14] 石达顺,唐朝晖. 基于统计高斯拟合的圆形光斑中心定位方法[J]. 测控技术,2020,39(7):51 − 56. [SHI Dashun,TANG Zhaohui. Circular spot center location method based on statistical Gaussian fitting[J]. Measurement & Control Technology,2020,39(7):51 − 56. (in Chinese with English abstract)] SHI Dashun, TANG Zhaohui . Circular spot center location method based on statistical Gaussian fitting［J］. Measurement & Control Technology,2020 ,39 （7 ）:51 −56 . （in Chinese with English abstract）[15] 陈航,张贝贝,旷华江,等. 基于BP神经网络反演分析的隧道塌方机理研究[J]. 水文地质工程地质,2023,50(3):149 − 158. [CHEN Hang,ZHANG Beibei,KUANG Huajiang,et al. A study of the tunnel collapse mechanism based on the BP neural network inversion analysis[J]. Hydrogeology & Engineering Geology,2023,50(3):149 − 158. (in Chinese with English abstract)] CHEN Hang, ZHANG Beibei, KUANG Huajiang, et al . A study of the tunnel collapse mechanism based on the BP neural network inversion analysis［J］. Hydrogeology & Engineering Geology,2023 ,50 （3 ）:149 −158 . （in Chinese with English abstract）[16] 邵毅明,钟颖,吴文文,等. 基于熵权TOPSIS法的短时交通流预测模型性能综合评价[J]. 重庆理工大学学报(自然科学),2020,34(7):205 − 211. [SHAO Yiming,ZHONG Ying,WU Wenwen,et al. Comprehensive evaluation of short-term traffic flow prediction model based on entropy TOPSIS model[J]. Journal of Chongqing University of Technology (Natural Science),2020,34(7):205 − 211. (in Chinese with English abstract)] SHAO Yiming, ZHONG Ying, WU Wenwen, et al . Comprehensive evaluation of short-term traffic flow prediction model based on entropy TOPSIS model［J］. Journal of Chongqing University of Technology （Natural Science）,2020 ,34 （7 ）:205 −211 . （in Chinese with English abstract）[17] 严干贵,宋薇,杨茂,等. 风电场风功率实时预测效果综合评价方法[J]. 电网与清洁能源,2012,28(5):1 − 6. [YAN Gangui,SONG Wei,YANG Mao,et al. A comprehensive evaluation method of the real-time prediction effects of wind power[J]. Power System and Clean Energy,2012,28(5):1 − 6. (in Chinese with English abstract)] YAN Gangui, SONG Wei, YANG Mao, et al . A comprehensive evaluation method of the real-time prediction effects of wind power［J］. Power System and Clean Energy,2012 ,28 （5 ）:1 −6 . （in Chinese with English abstract）[18] 殷坤龙. 滑坡灾害预测预报[M]. 武汉:中国地质大学出版社,2004:1 − 3. [YIN Kunlong. Landslide hazard prediction and evaluation[M]. Wuhan:China University of Geosciences Press,2004:1 − 3. (in Chinese)] YIN Kunlong. Landslide hazard prediction and evaluation[M]. Wuhan: China University of Geosciences Press, 2004: 1 − 3. （in Chinese）
-
期刊类型引用(2)
1. 石化波，王刚，曾怀恩. 一种ICEEMDAN-CNN-SVR滑坡位移组合预测模型. 三峡大学学报(自然科学版). 2025(01): 37-43 . 
百度学术
2. 李龙灿，吴鑫，刘永红，海英，张满，张龙梅，黄成佳. 松散堆积体斜坡变形-滑移过程的声发射特征参数演化规律. 中国地质灾害与防治学报. 2024(05): 151-159 . 本站查看
其他类型引用(1)
计量
- 文章访问数: 117
- HTML全文浏览量: 25
- PDF下载量: 92
- 被引次数: 3
邮件订阅
RSS