Study on the method for determining the position of landslide slip surface based on “D” type inclinometer curve
-
摘要:
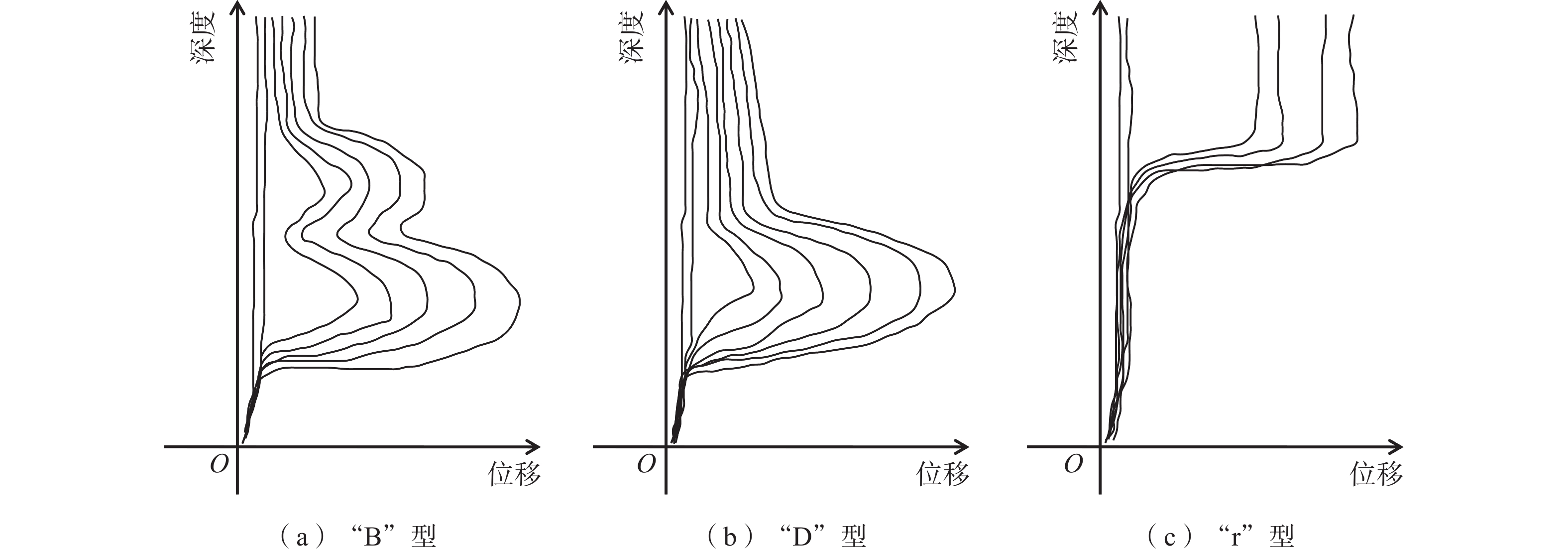
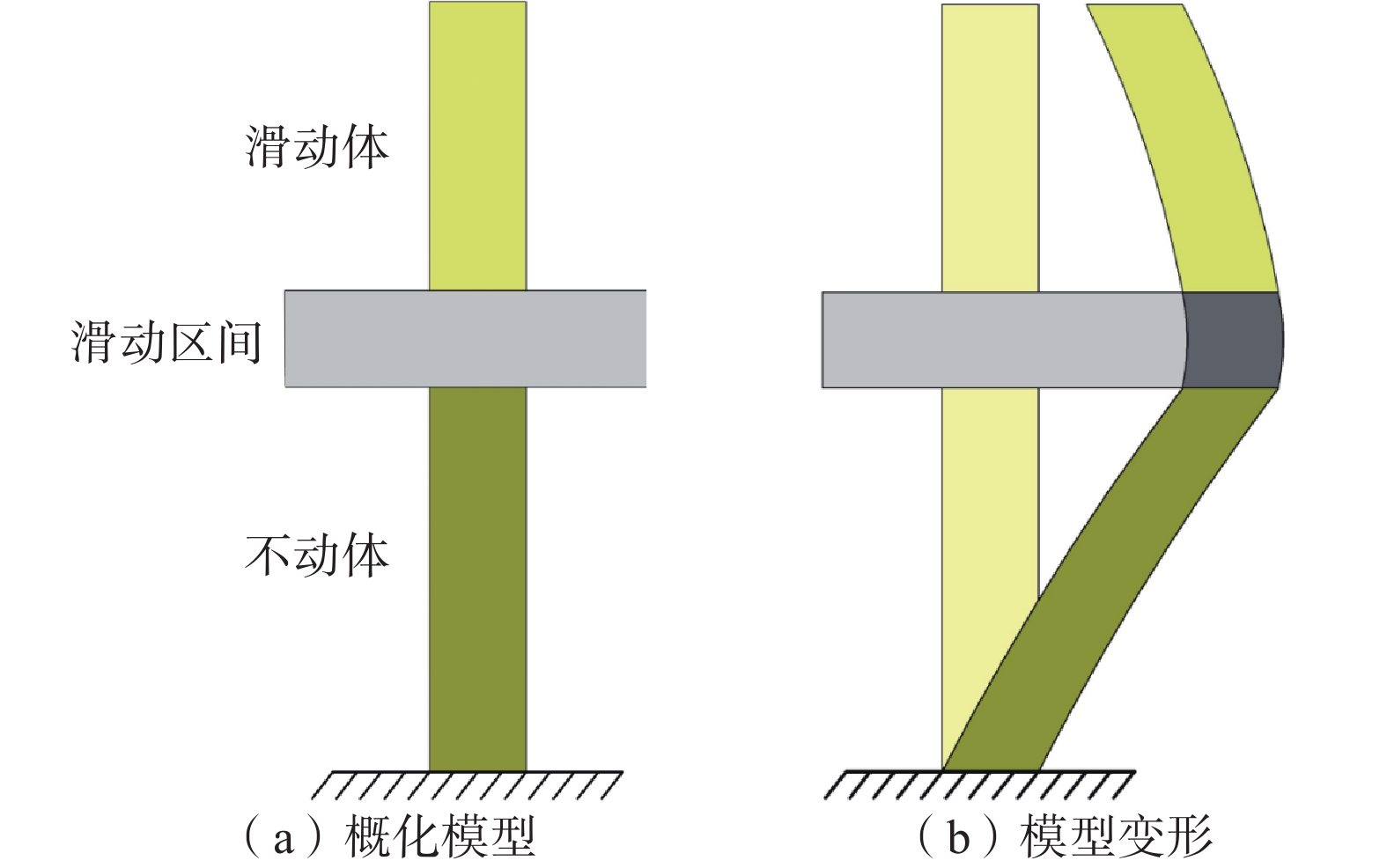
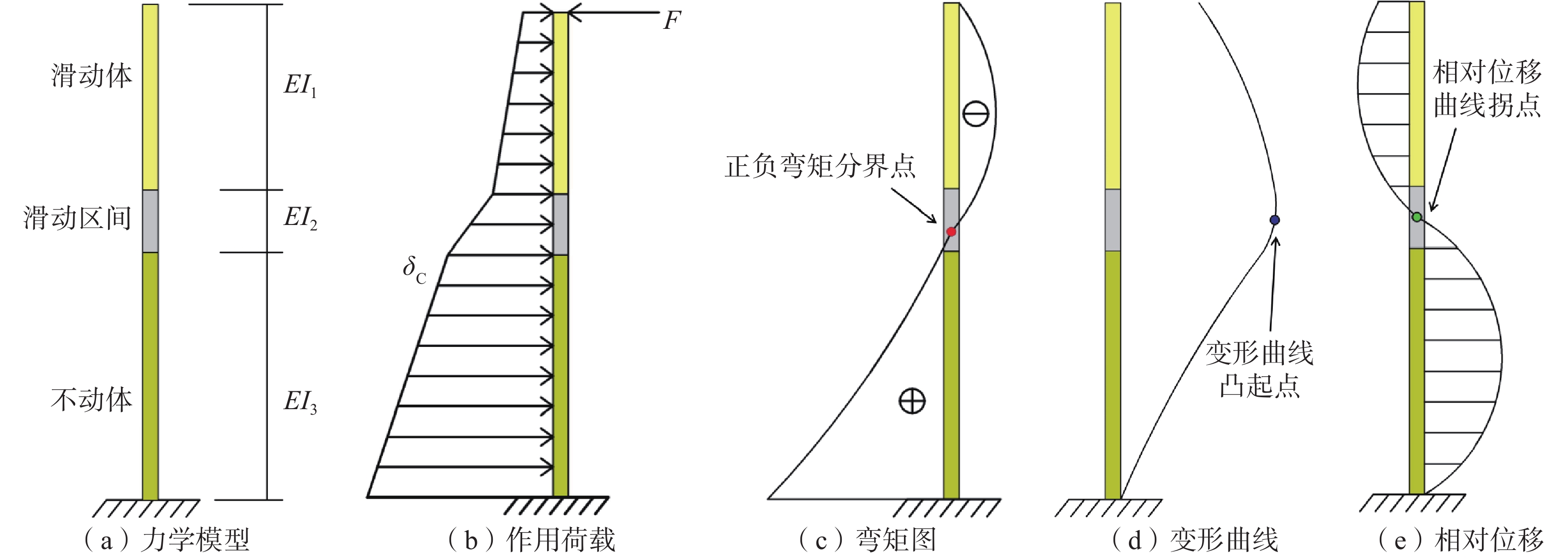
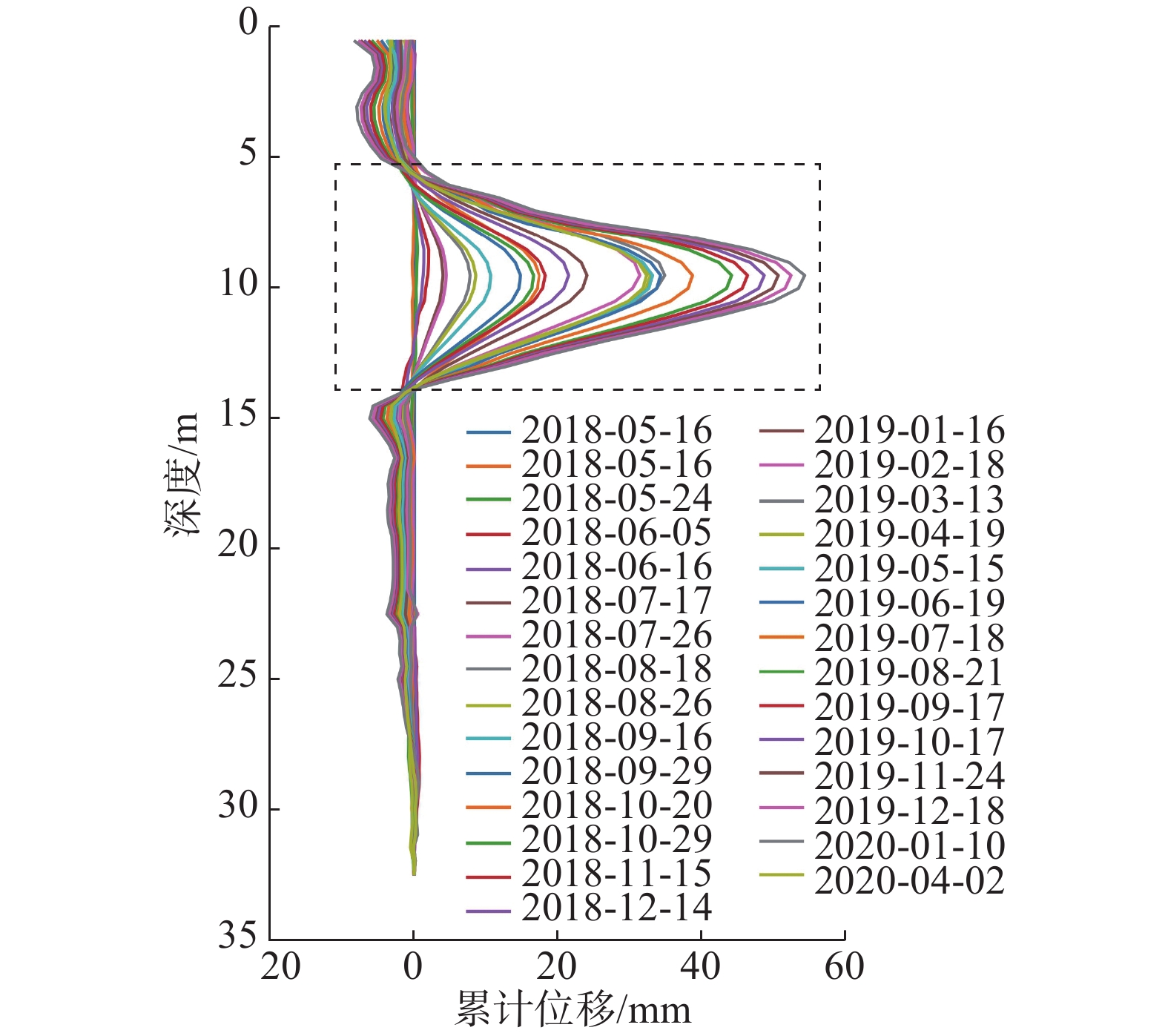
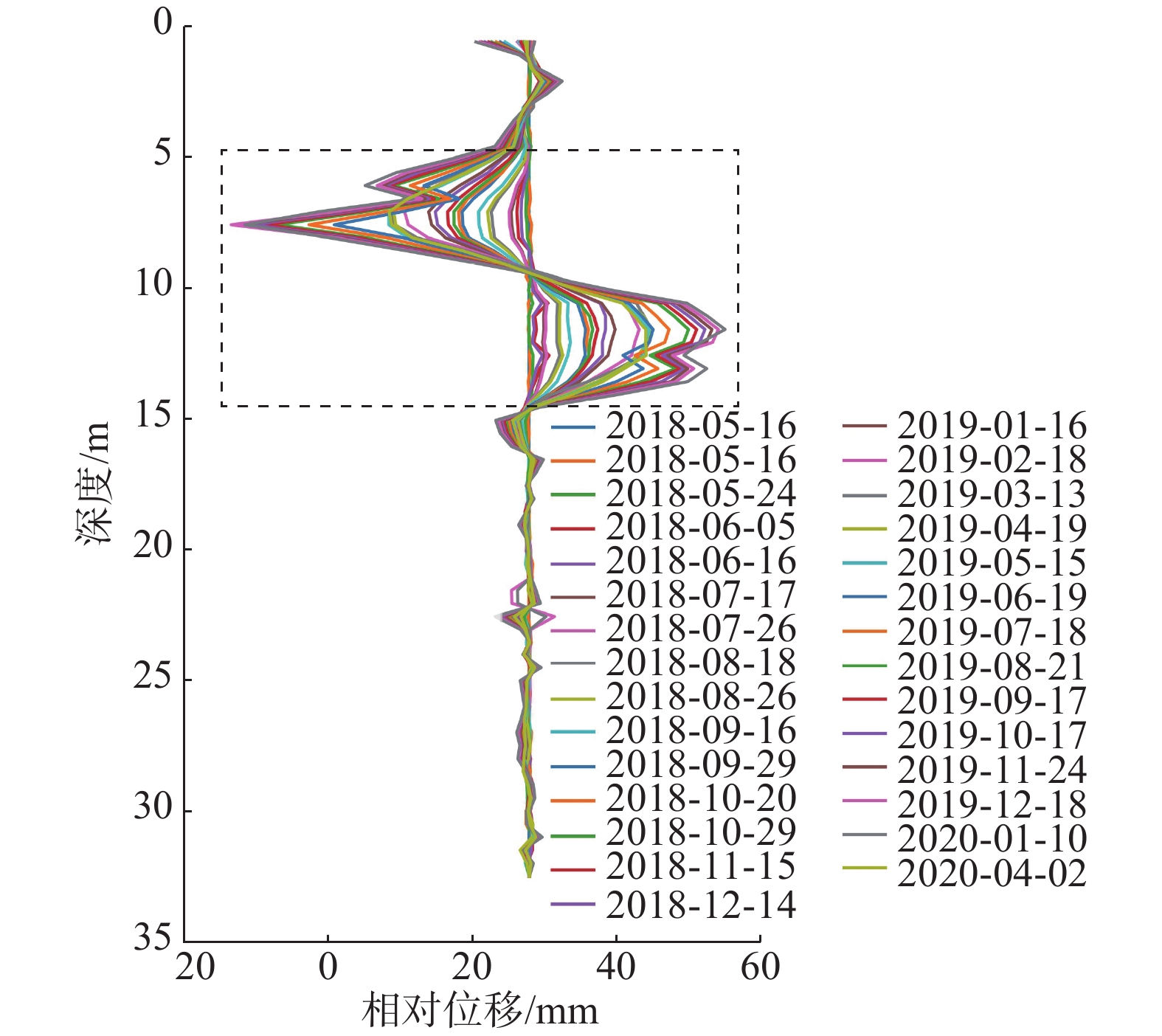
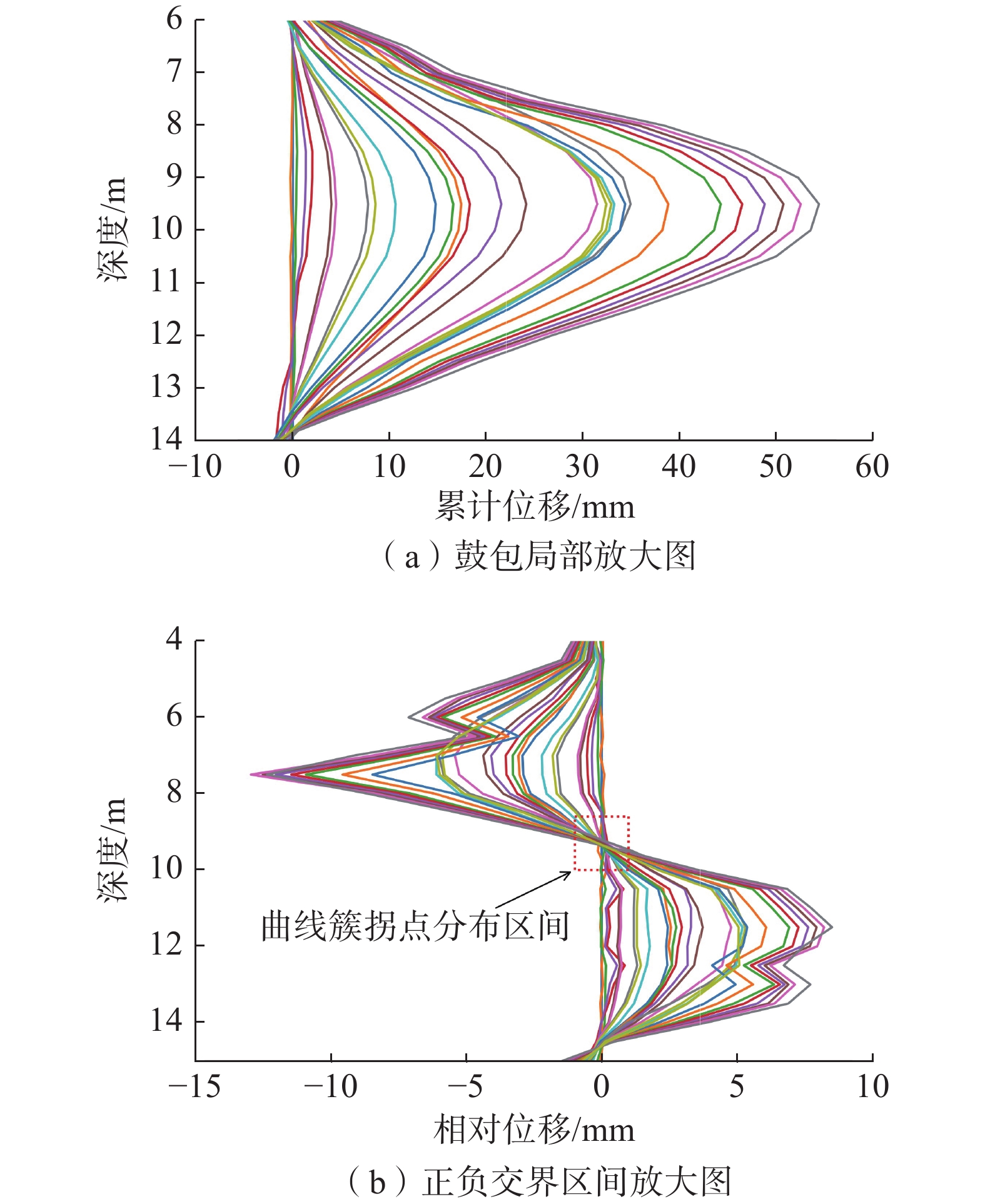
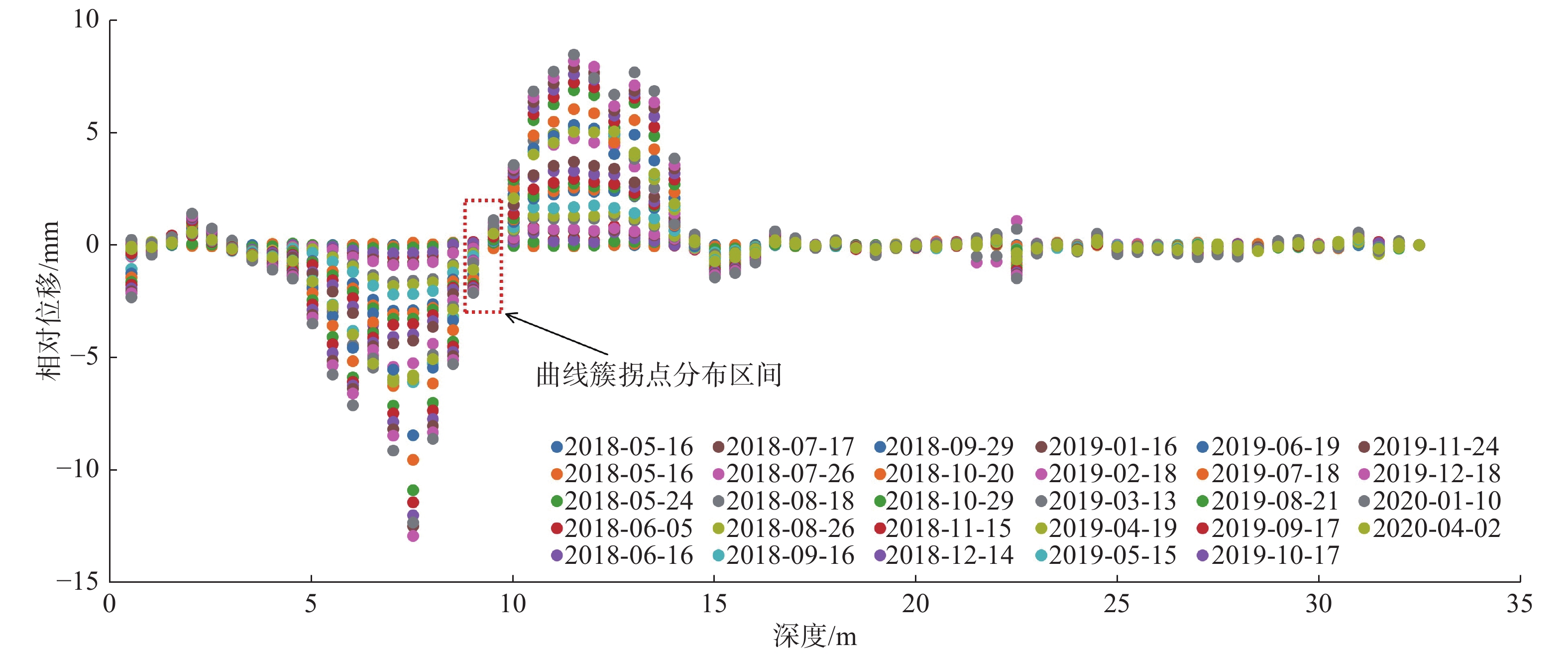
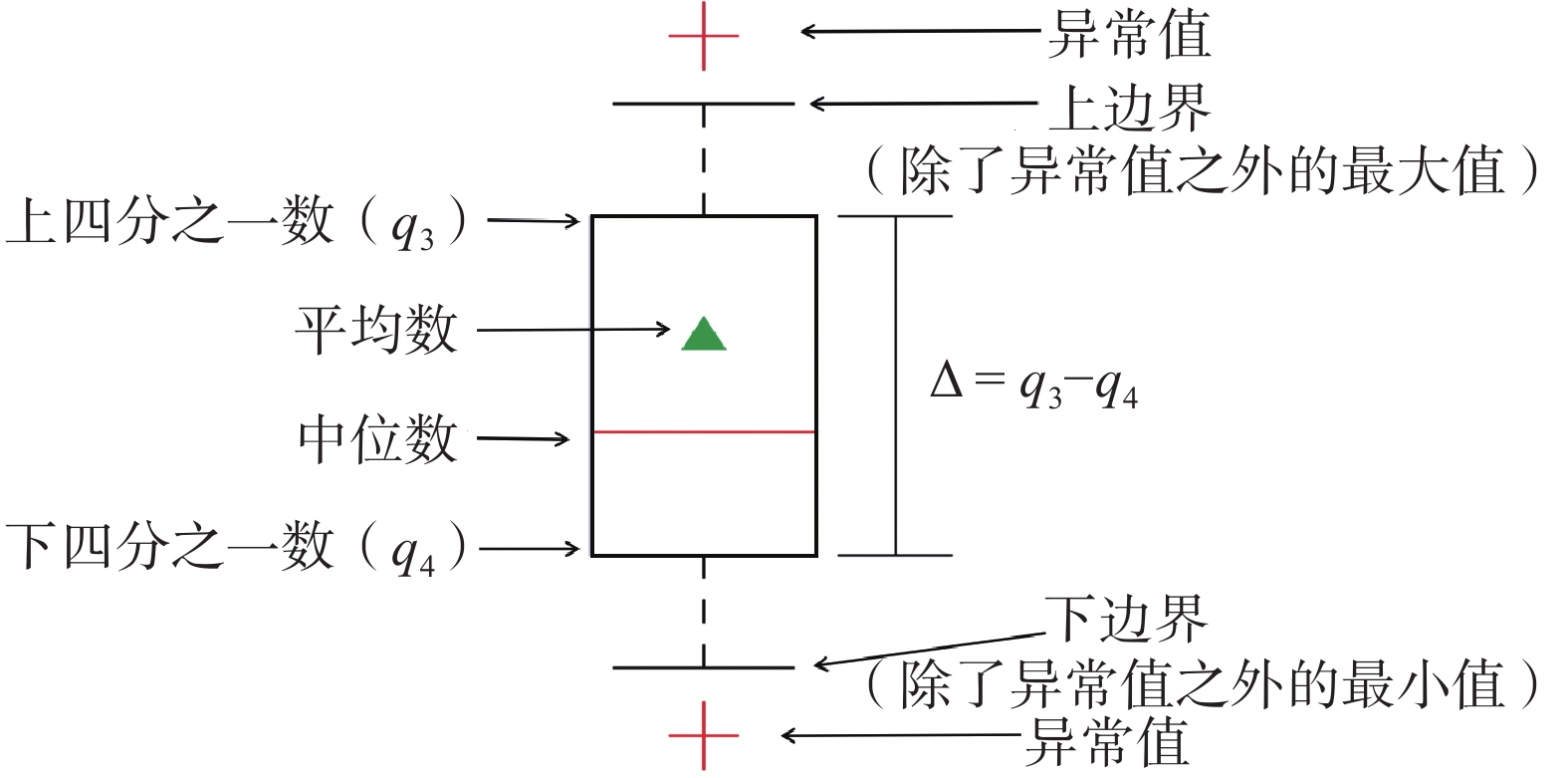
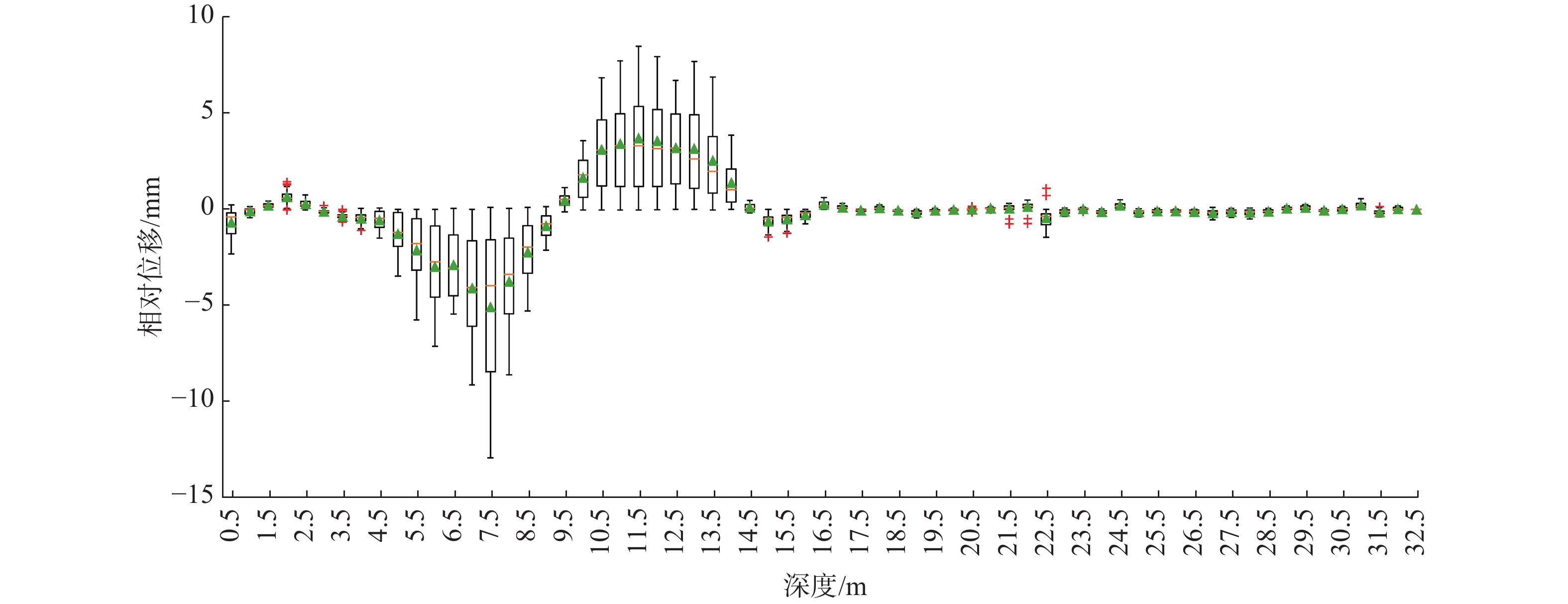
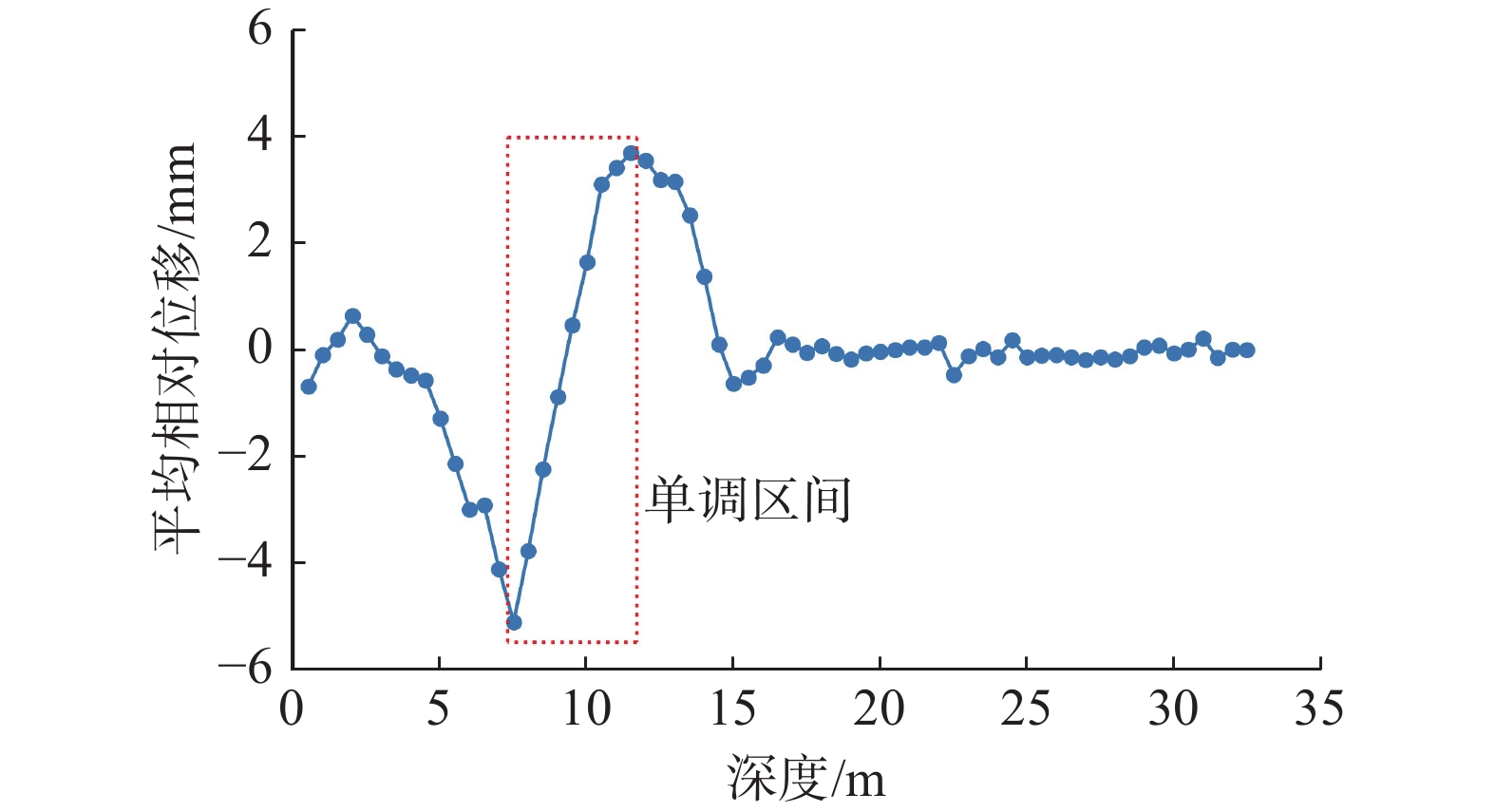
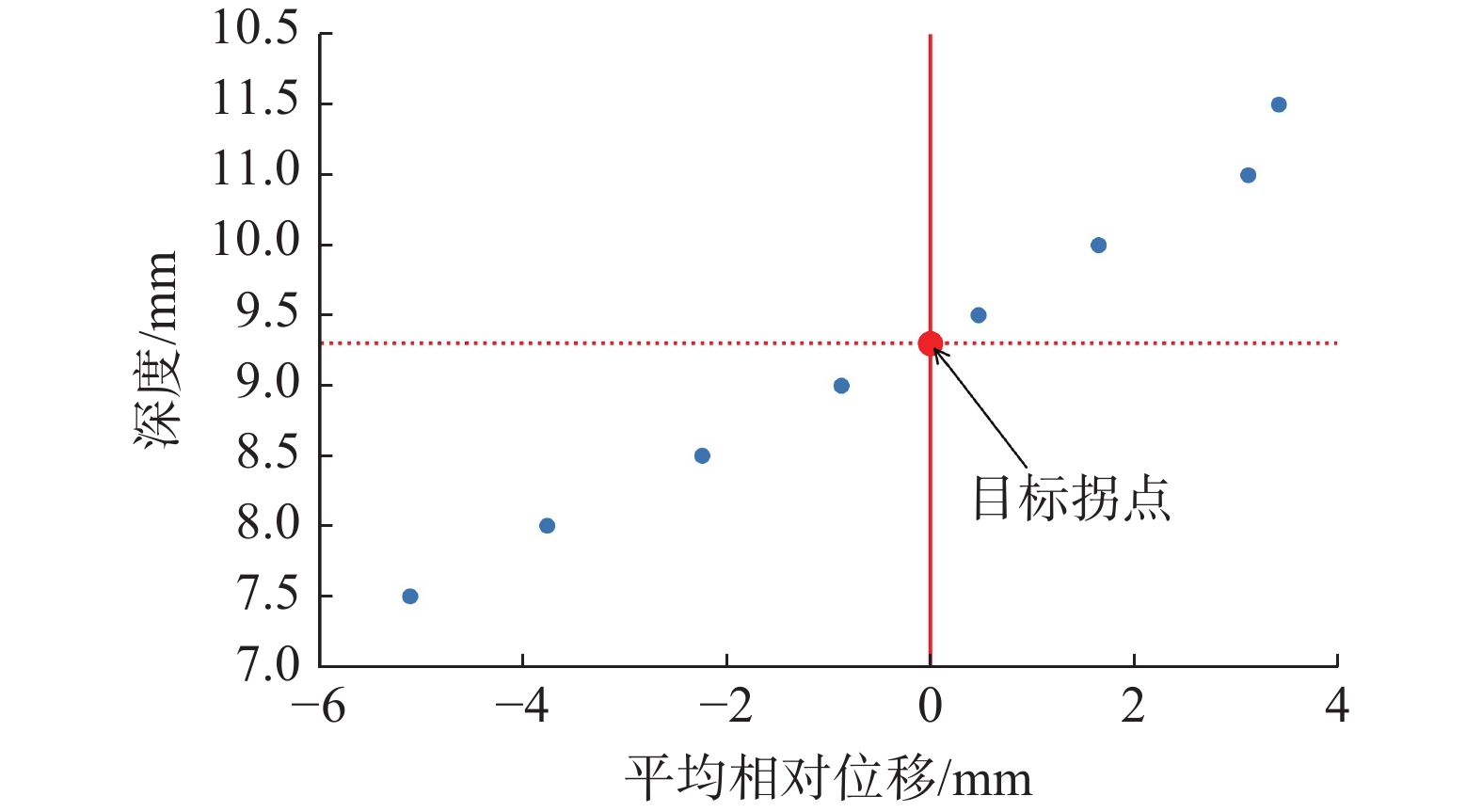
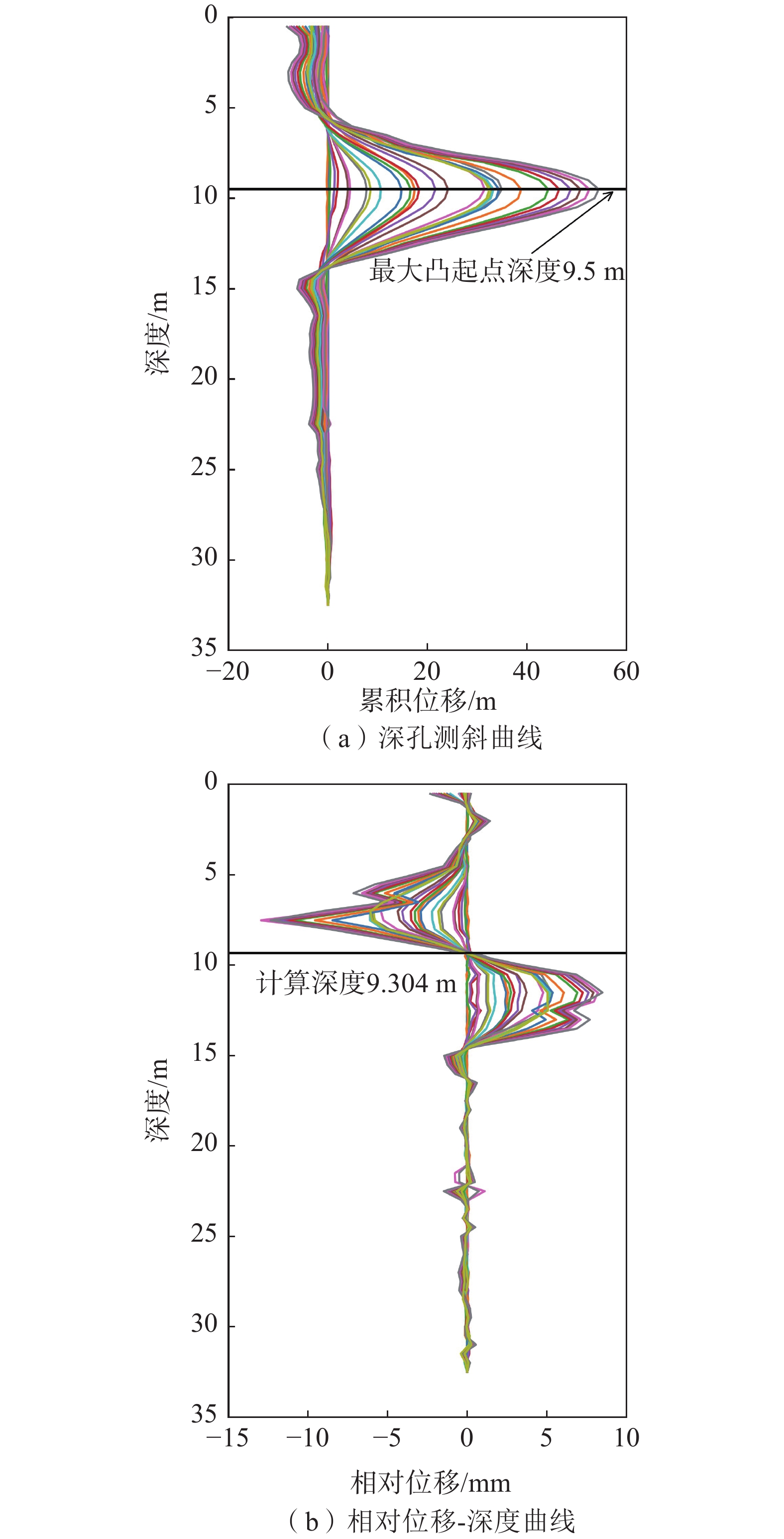
在实际的深孔位移监测中，测斜曲线的突变特征是滑动面辨识的关键依据，前人通过大量的研究总结将滑动面迹象显著的测斜曲线类型分为了“B”型、“D”型、“r”型等几种。其中，对于“D”型测斜曲线通常是将曲线的鼓包凸起点作为滑动面的位置，但这种方法容易受到测点布置间隔和横纵坐标观测尺度的影响，存在滑面位置定义不清晰、数值不确定的问题。为了能够有效地克服这些缺点，提升测斜曲线滑动面辨识的准确度，基于“D”型测斜曲线变化特征，将滑坡抽象为由“滑动体”“滑动区间”以及“不动体”三者组成的概化模型，根据三者抗弯刚度的差异建立外界荷载作用下的杆件力学模型，深入分析滑坡运动过程中不同深度处土体的变形特点。研究表明，由于“D”型曲线滑动面并未完全贯通，使得土体沿深度方向变形连续无突变，力学模型中杆件正负弯矩的分界点是变形曲线水平位移最大处，能够真实地反映滑坡变形特点以及滑动面的位置。将土体累计位移转化为相对位移，则“D”型深孔测斜曲线变为了“S”型相对位移-深度曲线，且“S”型曲线的拐点与滑动面的位置相近；通过提取监测期内不同深度处土体的平均相对位移，运用三次样条插值法计算“S”型区段内拐点的深度值，能够更加精准地确定滑动面位置，更好地提升深孔位移监测的可靠度和准确度，具有较大的实用价值。
Abstract:In borehole monitoring for deep displacement, the abrupt characteristics of inclinometer curves are the key basis for identifying the sliding surface. Previous studies have summarized several types of inclinometer curve patterns that exhibit significant sliding surface signals, including “B” “D”and “r” types. For “D” type inclinometer curves, the convex point of the curve is typically used as the position of the sliding surface. However, this method is susceptible to the influence of observation points spacing and coordinate observation scales, which can result in an unclear definition of the sliding surface position and uncertain numerical values. To overcome these drawbacks and improve the accuracy of sliding surface identification in inclinometer curves, a generalized model of landslides composed of “sliding body” “sliding interval” and “immovable body” was developed based on the variation characteristics of the “D” type inclinometer curve. A mechanical strut model subjected to external loads was established based on the different flexural rigidity of the three members, and the deformation characteristics of soil at different depths during landslide movement were analyzed in depth. The study found that the sliding surface of “D” curve does not entirely penetrate, leading to continuous soil deformation along the depth direction without abrupt change. The demarcation point of the positive and negative bending moments in the mechanical model is a location where the horizontal displacement of deformation curve is the largest, which can reflect the real deformation characteristics of the landslide and the position of the sliding surface. By converted the accumulated soil displacement into relative displacement, the “D” type inclinometer curve is transformed into “S” type relative displacement-depth curve, and the inflection point of the “S” type curve is close to the position of the sliding surface. By extracting the average relative displacement of soil at different depths during the monitoring period and calculating the depth value of the inflection point in the “S” type segment by using the cubic spline interpolation method, the position of the sliding surface can be determined more accurately, which can greatly improve the reliability and accuracy of deep displacement monitoring and has significant practical value.
-
0. 引言
堵塞效应在泥石流运动过程中是一种常见的现象，当泥石流流量不足以克服其阻力运动时，只有通过流量的积累以克服阻力，便产生了泥石流堵溃效应[1]。主支沟交汇[2-3]，沟道地形突变[4-6]以及沟道内的崩滑堆积体[7-9]均可使泥石流在局部产生堵溃效应，其宏观表现形式为沟道短暂断流与阵流现象[10-12]。汶川地震以后，由于沟道内大量崩滑体堵塞沟道，沟道断面束窄形成局部卡口地貌，泥石流的堵溃效应加显著，泥石流的堵塞系数相比震前显著增大[13]，泥石流堵塞系数取值范围由1～2.5 增大到2.0～5.5[14]，在计算泥石流防治工程设计流量时，胡卸文等[15]建议堵塞系数取值至少取值1.5，最大值可达4.0以上。崔鹏等[16]把震后泥石流堵塞系数普遍提高的主要原因归结于沟道微地貌的突变，主沟串珠状崩滑堰塞体级联溃决以及沟道束窄形成的卡口效应是导致泥石流发生堵溃效应和规模放大的核心因素[17]。另外，是否有支沟泥石流汇入或卡口处巨石堵塞也是泥石流规模放大的关键因素[18-19]。近几年以来，部分学者开始对堵溃效应及其产生的流量放大效应进行研究[20-21]，从冲刷系数、泥石流流量与流速、地形突变段长度以及泥石流级配对泥石流堵溃效应的影响等方面开展了理论探讨和试验研究。
天然泥石流沟道为一系列弯道与顺直段，宽窄相同的地貌组合，尤其在构造活动强烈，岩性软硬相间的地质条件下，更有利于卡口这种微地貌的形成。宽窄组合的卡口地形特征，更易引发泥石流的局部堵塞与溃决现象，从而产生泥石流流量放大效应[22-25]，泥石流造成的危害也更加严重。泥石流堵塞系数是表征泥石流堵溃效应的特征参数，也是泥石流防治工程勘察设计规范中配方法计算泥石流流量的关键参数。现行规范中往往以卡口的多少作为泥石流堵塞程度的判定依据，具有明显的经验性，未考虑泥石流体性质、泥石流的运动特征以及卡口微地貌形态对卡口堵溃效应和堵塞系数的影响，导致泥石流流量计算存在较大的不确定性，从而影响泥石流防治工程的效果与运行安全。
文中尝试通过模型试验的方法，探索不同卡口地形和泥石流特征条件下，泥石流发生堵溃的临界条件，分析卡口段泥石流流量的放大效应，对于完善泥石流防灾减灾技术规程，提高对泥石流运动堆积过程的认知，具有重要的理论意义和应用前景。
1. 泥石流卡口堵溃试验设计
1.1 桦头尖泥石流概况
1.1.1 气象与水文条件
什邡市位于四川盆地边缘及边缘山区，属亚热带湿润季风气候，区内气候随地势变化差别较大。总体特征是天气温湿、雨量充沛、四季分明。夏季多暴雨；秋季气温降幅大，多连绵阴雨；冬季长，气温低日照少，常有低温、冰雹等自然灾害发生。
根据什邡市气象站多年观测资料，区内多年平均气温13.6 °C。年最冷为1月，平均气温3.7 °C，极端最低气温−8 °C（1984年）；最热为7—8月，平均气温23 °C，极端最高气温35.5 °C（1996年）。多年平均月最大降水量为254.36 mm，多年平均月最小降水量4.49 mm（表1），年均总降水量938.9 mm。每年降雨多集中在5—8月，占全年降水量的76%。降雨分配极度不均匀，局部地段暴雨频繁，且随地势增高，降雨量明显增加，山区降雨和平原区形成较大差异。
表 1 什邡市多年平均月降水量统计表（1971—2002年）Table 1. Statistical table of annual average monthly precipitation in Shifang City （1971—2002）月份 l 2 3 4 5 6 7 8 9 10 11 12 降水量/mm 11.85 20.34 44.58 75.81 114.67 254.36 202.44 141.69 36.31 15.77 4.49 11.85 根据《四川省中小流域暴雨洪水计算手册》所附暴雨量等值线图，什邡市红白镇地区的1/6 h、1 h、24 h多年最大暴雨量平均值分别为8.3 mm、20 mm、60 mm，变异系数分别为0.51、0.35、0.48, 查皮尔逊Ⅲ型曲线得到不同频率下模比系数并求得不同频率下的雨强值统计见表2。
表 2 研究区不同频率下雨强值计算表Table 2. Calculation table of rain intensity values at different frequencies in the study area频率/% 10 min雨强 1 h雨强 6 h雨强 24 h雨强 平均值
/mm变异
系数模比
系数设计雨强
/mm平均值
/mm变异
系数模比
系数设计雨强
/mm平均值
/mm变异
系数模比
系数设计雨强
/mm平均值
/mm变异
系数模比
系数设计雨强
/mm1 12.5 0.4 2.31 28.88 45 0.35 2.11 94.95 100 0.5 2.74 274.00 160 0.58 3.1 496.00 2 2.08 26.00 1.92 86.40 2.42 242.00 2.69 430.40 5 1.78 22.25 1.67 75.15 1.99 199.00 2.16 345.60 10 1.53 19.13 1.47 66.15 1.66 166.00 1.75 280.00 四川山区泥石流激发雨量一般为一次雨量48～50 mm或10 min雨量8～12.2 mm。由于地震后，桦头尖沟内不良地质现象发育，松散物源量大增，其激发雨量还可能更低。桦头尖沟区域内降雨较丰沛，且雨量集中，其雨强完全可以满足激发泥石流的条件，暴雨是该泥石流的主要引发因素。
桦头尖沟为常年流水溪沟，主要接受大气降水补给，流量受降水量控制，冬春季节有融雪补给，但融雪补给水量较少，泥石流均为雨季暴发，融雪不构成泥石流主要水源。
1.1.2 地质环境条件
桦头尖沟流域属深切割构造侵蚀低山和中山地形，“V”型谷，沟谷平面上较为顺直，沟道总体比较狭窄，一般在5～10 m，出山口后沟道有所展宽，在10～20 m。主沟长1.6 km，流域内最高点高程为1720 m，沟口与唐家河交汇处高程为1096 m，相对高差624 m，主沟平均纵坡降392.3‰，其中上游沟道陡峻，切割深度较大，平均纵坡400‰以上，下游沟段纵坡略缓，平均纵坡190‰～310‰。地形陡峻，地形临空条件发育，为流域内崩塌、滑坡等不良地质现象的发育，以及为泥石流松散固体物源的汇集提供了有利条件。特别是在5.12地震后，沟内新产生了大量的崩滑等不良地质体，为泥石流的发育提供了大量松散固体物源。
沟道上游，沟谷较为狭窄，纵坡较陡，水流湍急，且动态变化较大，具陡涨陡落的山溪沟谷特征。森林植被在地震中遭到严重破坏，覆盖率有所降低，地震中不良地质现象极其严重，松散堆积层覆盖较厚，主要为基岩斜坡崩塌堆积物，可参与泥石流活动的松散物源量相对较多。
沟道中游，两侧岸坡陡峻，为砂岩、粉砂岩泥岩互层，岸坡坡度一般50°～60°，局部沟道直立甚至反角；沟内发育多处陡坎和深潭，沟床基岩出露，沟床粗糙，沟内有巨石和携带的树木堆积以及茂密的灌丛，植被覆盖较好；崩滑不良地质体较为发育，主要为第四系残坡积滑坡及坡面侵蚀堆积物；沟道堆积物主要为巨大漂石，大部分沟床基岩裸露；崩滑体发育处沟道堵塞严重，堆积物厚1～3 m。
沟道下游，为泥石流和冲洪积堆积扇形地，形状比较规则，保存较好。堆积扇前缘有唐家河通过，沟口距唐家河高差约为20 m。
1.2 试验装置
试验水槽装置主要由三部分组成：泥石流供料箱、试验水槽及集水池（图1）。
供料箱：位于顶部，为横截 边长50 cm的正方形，高80 cm，供料箱上部设置最大开度20 cm的闸门与试验水槽相接，下部焊接锥形漏斗，最大供料体积150 L。每次试验时，记录供料箱内物料的高度，从而计算出泥石流的流量过程。
试验水槽：位于中部，为双面钢化玻璃水槽，长4.5 m，横截面高40 cm，宽30 cm，纵坡可通过龙门架在6°～12°之间调节，水槽卡口部位两侧贴透明网格纸，通过高速摄像机记录泥石流的运动参数。
集水池：位于尾部，为长80 cm、宽80 cm、高60 cm的砖砌水池，用以收集泥石流堆积体。
供料箱及集水池通过水位传感器记录水位变化，并通过体积法分别计算入口和出口处泥石流的流量，其中Qe/（L·s−1）为入口流量，Q/（L·s−1）为出口流量。
1.3 卡口模型的制作
卡口模型采用混凝土制作，并使用模具制作成不同的形态，在试验中共制作了3中不同形态的卡口，即V形卡口、矩形卡口和梯形卡口，并通过卡口宽度（w）和倾角（α）控制卡口的大小，卡口以水槽中轴线对称布置于水槽出口处上游1/3处。
1.4 泥石流试样的配制
泥石流试样模型砂的配制主要参考桦头尖2011年4种不同泥石流堆积物的级配特征，并按照1∶100的几何相似性比尺进行缩放；考虑到颗粒级配的连续性与分形相似性，试验中选取粒径小于20 mm的部分进行试验；同时，为了在试验中能够更好地观测松散颗粒的堵塞和运动过程，对不同粒径组的泥沙颗粒分别进行染色处理。泥石流试样的容重采用称重法确定，试验中采用的模型砂级配曲线如图2所示。
1.5 试验方法和步骤设计
利用水槽试验，探讨沟域特征和不同性质下的泥石流，通过不同的形态卡口时泥石流的堵溃过程与流量放大效应。试验步骤如下：
①按照预定级配与泥石流容重，分别对模型砂与水进行称重，通过搅拌机充分，然后通过标准工具测量容重；
②调整水槽坡度至试验预定值；
③准备好所有测量仪器与记录装置；
④首先不设置卡口，分析顺直沟道泥石流的运动过程。
a. 试验开始时利用数码摄像机录制试验过程，以测量泥石流泥深，龙头流速及流态，并记录床沙启动过程；
b. 使用数码摄像机和水位计记录集水池的水位变化以获得泥石流的流量过程，并于未设置卡口时的流量过程进行对比分析；
c. 测量水槽内泥石流的冲淤测量，摄影并绘制冲蚀—堆积关系图。
d. 对水槽内的泥石流冲蚀—堆积物进行取样，送试验室分析。
⑤在试验水槽设置卡口，重复④a—d；
⑥改变其他试验条件，重复①—⑥。
卡口段泥石流堵溃过程试验从2020年6月开始至2021年10月，共进行试验9组31次。其中无卡口对比试验6次（SY0-1—SY0-6），正式试验8组25次，各组次试验参数如表3所示。其中变量为卡口宽度（w）、卡口扩展角（a）、束窄率（Ar）、卡口长度（L）、颗粒中值粒径（D50）、泥石流容重（γd）、松散物源（Vs）。
表 3 试验组次安排表Table 3. Schedule of test groups组次 卡口形态 泥石流特征 沟域特征 松散物源
/（10−3m3）卡口形状 卡口宽度
/cm卡口扩展角
/（°）束窄率 卡口长度
/cm颗粒中值
粒径/mm泥石流容重
/（kN·m−3）沟道纵坡
/（°）SY0-1 3.458 18.27 6 无 SY0-2 3.458 18.27 9 无 SY0-3 3.458 18.27 12 无 SY0-4 3.458 18.27 6 无 SY0-5 3.458 18.27 9 无 SY0-6 3.458 18.27 12 无 SY1-1 矩形 12.5 — 0.250 30 3.458 18.27 9 无 SY1-2 10 — 0.333 SY1-3 7.5 — 0.417 SY2-1 V形 60 0.268 30 3.458 18.27 9 无 SY2-2 45 0.413 SY2-3 30 0.567 SY3-1 梯形 （10,20） 0.5 30 3.458 18.27 9 无 SY3-2 （10,10） 0.67 SY4-1 梯形 （10,20） 0.5 20 3.458 18.27 9 无 SY4-2 30 SY4-3 40 SY5-1 梯形 （10,20） 0.5 30 3.458 16.85 9 无 SY5-2 18.27 SY5-3 19.62 SY5-4 20.35 SY6-1 梯形 （10,20） 0.5 30 1.734 18.27 9 无 SY6-2 3.458 SY6-3 5.264 SY6-4 9.935 SY7-1 梯形 （10,20） 0.5 30 3.458 18.27 6 无 SY7-2 9 SY7-3 12 SY8-1 梯形 （10,20） 0.5 30 3.458 18.27 9 3.37 SY8-2 6.74 SY8-3 10.11 注：（10，20）分别代表梯形卡口底宽与顶宽。 2. 卡口段泥石流堵溃过程的影响因素
卡口段泥石流的堵塞与溃决过程与卡口的几何形态、泥石流流体特征以及沟域特征有密切的关系，文章通过单因素试验的方法，探讨上述因素对卡口段泥石流运动与堆积过程的影响。
2.1 卡口几何形态
泥石流流经卡口段时，泥石流的运动状态与参数发生明显改变，且与卡口形态和卡口束窄率具有较大的相关性。
2.1.1 洪峰流量衰减
泥石流流经卡口段时，由于沟道过流断面变小，在卡口内存在急流冲刷现象，但在卡口段上游大量堆积物从泥石流流体中析出，固体颗粒大量沉积，
泥位变大，并有显著表面粗化现象；通过卡口后，泥石流的固体物质出现轻微分选，出口处泥石流峰值流量相对于无卡口段时，出现了显著的衰减（图3）。为了探讨泥石流通过卡口段流量的变化大小，定义无量纲参数流量比Qpr：
![]()
图 3 不同形态卡口条件下泥石流的流量过程线Figure 3. Discharge hydrograph of debris flow through different bayonets(1) 式中：Qpo——闸门出口处泥石流峰值流量/（L·s−1）；
Qpi——料箱泥石流出流峰值流量/（L·s−1）。
不同类型的卡口对泥石流通过卡口前后峰值流量的影响有所不同，矩形卡口流量比0.512～0.765，V形卡口流量比0.534～0.844，梯形卡口流量比0.788～0.909。同时，试验结果表明，卡口段泥石流流量的衰减与卡口断面的束窄率呈负相关关系，即卡口处断面相对于上游沟道变窄程度越大，泥石流流量衰减程度越高，可近似采用线型关系表示（图4）：
![]()
图 4 卡口束窄率与流量比的关系Figure 4. The relation between narrowing rate of bayonet and discharge ratio(2) (3) 式中：Ar——卡口束窄率；
Ak——卡口段水槽横断面面积/cm2；
Ag——无卡口水槽断面面积/cm2。
从试验结果可知，泥石流流经卡口微地形时，泥石流流量会发生衰减，且卡口处地形断面相对于沟道上游断面变化越大，则流量越易产生衰减。
2.1.2 洪峰展平
相对于无卡口时，各组次试验泥石流通过卡口后，流量过程线均出现洪峰展平的现象（图3），一次泥石流过程持续时间延长，洪峰出现时刻延后，且延后时间（Td/s）与流量比以及卡口断面束窄率呈正相关关系，即卡口处断面束窄程度越大，泥石流峰值流量滞后时间越长，可近似采用指数关系表示（图5）：
![]()
图 5 卡口束窄率与峰值流量延迟时间的关系Figure 5. The relation between narrowing rate of bayonet and delay time of peak discharge(4) 试验中采用了三种不同纵向长度的卡口，用以探讨卡口段长度的变化对泥石流运动参数的影响，试验结果显示：卡口的长度的增加会增大泥石流流量衰减的过程，会减缓峰值流量出现时时刻，但不同卡口段长度时，泥石流通过卡口段的流量过程线并无明显区别，卡口段长度对泥石流运动参数的影响较小（图6）。
![]()
图 6 不同卡口长度的泥石流流量过程线Figure 6. Discharge hydrograph of debris flow with different bayonet lengths2.2 泥石流流体特征
2.2.1 泥石流容重
试验结果表明（图7），泥石流容重与固体颗粒体积比浓度越大，其运动阻力越大，流速越慢，泥石流在遭遇卡口段时，越易产生堆积作用，泥石流在卡口段的流量衰减过程越显著；同时，随着泥石流容重的增大，泥石流峰值流量出现时刻也越晚，洪峰展平的现象也越显著。
![]()
图 7 不同容重泥石流通的流量过程线Figure 7. Discharge hydrograph of debris flow with different bulk density2.2.2 泥石流级配
泥石流颗粒级配对卡口段的泥石流运动过程也有较大影响（图8）。颗粒粒径越粗，同等水力条件下，遭遇到卡口后，卡口上游段泥石流固体可以更易发生堆积作用，致使通过卡口段的泥石流流量发生衰减，泥石流过流总量减小，但泥石流级配对卡口处泥石流峰值流量出现时刻的无较明显影响。
![]()
图 8 不同级配泥石流的流量过程线Figure 8. Discharge hydrograph of debris flow with different gradation2.3 沟域特征
从试验结果来看，水槽纵坡较大时，如图9（a），J=12°），泥石流排泄速度越快，卡口的存在对泥石流的运动过程影响较小，泥石流流量过程线越趋向于尖瘦型，泥石流固体物质在卡口段前不易发生堆积作用，卡口处出现急流冲刷现象，相应的泥石流通过卡口段时的流量衰减越小，卡口段前后流量比也越大，洪峰展平现象越不显著；水槽纵坡较小时,如图9（c）中曲线J=6°，卡口的存在致使一次泥石流持续时间延长，卡口段前部固体物质大量堆积，峰值流量出现时刻显著延后，洪峰展平现象也更为显著。通过分析不同坡度条件下，卡口段泥石流峰值流量的衰减率，可以发现：泥石流峰值流量的衰减与沟道坡度负相关、如图10所示，即沟道坡度越大，越不易产生流量衰减，相应的沟道坡度越小，则越易产生沟道局部堵塞的现象。
![]()
图 9 不同坡度条件下泥石流的流量过程线Figure 9. Discharge hydrograph of debris flow with different inclination同时，水槽纵坡也会影响峰值流量延迟的时间，坡度越大延迟时间越短，泥石流流量过程洪峰展平的迹象也越不显著。
2.4 沟道堆积物
野外调查表明，卡口段泥石流的堵溃过程与流量放大效应与滑坡堆积体、支沟泥石流堆积扇等坡地重力作用形成的半堵塞、全堵塞沟道密切相关，松散堆积物常堆积与沟道一侧，沟道多向对岸偏移或沟道局部侵蚀基准面抬高，从而形成堆积型卡口。试验中在水槽两侧堆放不同体积的堆积物，按照长度为20 cm的V形卡口布置于试验水槽卡口段，模拟堆积型卡口对泥石流堵溃作用的影响。
从试验结果来看（图11），当沟道内存在堆积型卡口时，虽然堆积型卡口的存在会耗散泥石流运动的动能，但由于堆积物大量进入泥石流浆体，泥石流流量有显著增大的趋势，峰值流量出现时刻延后，一次泥石流总量也显著增大。
![]()
图 11 不同体积的堆积型卡口段的流量过程线Figure 11. Discharge hydrograph through sediment bayonet with different volumes3. 卡口段泥石流的流量比
试验结果表明，泥石流流经卡口段时，若沟道内无松散物源的补给，则会产生流量衰减过流，泥石流峰值流量出现时刻延后，洪峰过程线展平；泥石流通过卡口段时其流量比主要与以下3个无量纲参数有关：γs/γd、w/D50、J/Ar，定义无量纲参数K综合表示，通过试验数据回归分析，卡口段泥石流流量比Qpr可表示为（图12）：
(5) 式中：γs/γd——泥石流相对容重；
w/D50——泥石流固体颗粒代表粒径与卡口的相对 大小；
J/Ar——泥石流潜在动能与卡口段能量耗散之间的 比值；
K——无量纲参数。
对于单位宽度、单位长度的水体在单位时间内所泥石流运动所提供的能量W可以表示为：
(6) 式中：γd——泥石流的容重/（kN·m−3）；
q——单宽流量/（L·s−1）；
J——能坡/（°）。
沟床床面的输沙浓度与水流提供的功率存在线性关系，即：
(7) 式中：Sv——以干容重计的单宽输沙率；
k——输砂常数；
We——特定粒径泥砂的启动功率，当坡度条件不变时，泥砂的启动功率为常数。
从式（6）可以得出，当泥石流流经卡口段时，沟道断面的突变，必然会引起由于克服卡口阻力而产生能量耗散，泥石流输砂浓度减小，泥石流固体物质析出，导致峰值流量衰减，因此式（5）中的K值实质上表征了泥石流流体动能与固体颗粒启动或堆积时的能量耗散之间的相互关系。
4. 结论
（1）文中通过试验分析了泥石流通过卡口段时，泥石流运动参数的变化以及卡口的堵塞效应。文中通过试验发现，泥石流通过卡口地形时，泥石流流量出现堵塞效应而产生的流量放大，或因为固体物质堆积而出现流量衰减，均与卡口部位的几何条件、泥石流特征、沟域特征、是否存在附加松散物源有关。当卡口附近无附加松散物源时，改变其他3个试验条件时，均出现了流量衰减的现象，即流量比Qpr<1；而堆积型卡口，由于有附加堆积物的，泥石流体积比浓度与一次泥石流总量的增大，3次试验中，有2次出现了流量的放大作用，即流量比Qpr>1（即试验S8-1—S8-3）。
（2）泥石流通过卡口段时，由于过流断面的减小，卡口上游段必然产生涌塞，局部流速减小，泥石流固体物质析出而堆积于沟道之上，致使泥石流通过卡口后出现流量衰减。从能量耗散的角度来看，卡口地形改变了泥石流运动的边界条件，导致能量的耗散；当无附加能坡或固体物质时，则必然会出现流量衰减的现象。
（3）泥石流流量计算方法的研究最早始于20世纪30年代，M.斯里勃內依采用雨洪修正法计算泥石流流量，并采用附加流量表示沟道堵塞效应，或通过堵塞系数表征泥石流流量的这种叠加效应，并在我国泥石流研究与防治工程设计中广泛应用。但对于某一具体流域的堵塞系数仍然是未知数，在定量取值上有很大的主观性和不确定性，目前一般认为泥石流的堵塞系数取值范围为1.0～3.0。文中所定义的流量比Qpr实质上即为泥石流在特定断面的堵塞系数，其取值在很多条件下并不是大于1的；因此，在沟道纵坡较小，卡口束窄率较大，而沟道内又无较多可活动物源的条件下，笼统地将堵塞系数取值大于1，缺乏合理性，容易引起泥石流防治工程超标设计，造成极大的投资浪费。
（4）卡口段泥石流堵塞现象成因复杂，本试验以野外试验成果级配构成基本试验参数，在野外调配基本浆体,但野外调配级配时并未考虑泥石流规模和固体物质来源方式与大颗粒物质等因素的影响，试验数据因大颗粒物质含量过少，明显的堵溃与冲淤现象在试验组次中相较野外原型可能存在数量变少的情况，从而对推导流量比产生间接影响。但通过文中的试验现象揭露，卡口的存在多为泥石流流量衰减的正面因素，而是否存在松散物质的加入则是卡口段泥石流的堵塞效应发生的关键因素。因此，在泥石流调查研究和防治工程勘查设计时，应更加侧重于堆积型卡口的形态、规模以及参与泥石流活动的方式，以期获得更加合理的泥石流运动参数。
-
![]()
图 1 深孔测斜曲线的特征类型
Figure 1. Schematic view of the characteristic types of deep-hole inclinometer curve
![]()
图 11 单调区间平均相对位移-深度散点图
Figure 11. Average relative displacement-depth scatter plot in Monotonic interval
![]()
图 13 “r”型曲线平均相对位移点线图
Figure 13. Point line diagram of the average relative displacement of the "r" curve
表 1 深孔测斜曲线典型类型
Table 1 Typical types of deep-hole inclinometer curve
曲线类型 坡体破坏类型 曲线特征 滑坡变形破坏情况 滑动面发展程度 钟摆型 倾倒变形 累计位移在整个深度范围内于初测值附近摆动，
摆动幅度一般小于10 mm滑坡岩土体的深部位移很小，
边坡处于稳定状态未贯通 “V”型 顺层溃屈 上部位移较大而底部位移很小，曲线总体呈线性特征 滑坡内部没有形成明显的滑动面，
处于蠕动变形阶段未贯通 “r”型 切层滑移、顺层滑移、崩塌 累计位移在一个较浅的位置产生较为明显的突变，
而其下部的位置则相对较小滑坡岩土体在浅部形成明显的滑动面 贯通 “D”型 切层滑移、顺层溃屈 累计位移在某一个较深的位置产生突变，
而其上部产生近似整体的移动滑坡深部产生了一个明显的滑动面 接近贯通 “B”型 顺层滑移 累计位移在多个位置产生较为明显的突变，
曲线呈现类似“阶梯”或“波浪”状滑坡岩土体内部形成了多个滑动面 接近贯通 
下载: 导出CSV
-
[1] 徐邦栋. 滑坡分析与防治[M]. 北京: 中国铁道出版社, 2001 XU Bangdong. Landslide analysis and prevention[M]. Beijing: China Railway Publishing House, 2001. （in Chinese）
[2] 陈开圣,彭小平. 测斜仪在滑坡变形监测中的应用[J]. 岩土工程技术,2006,20(1):39 − 41. [CHEN Kaisheng,PENG Xiaoping. Applications of inclinometer in monitoring deformations of landslide[J]. Geotechnical Engineering Technique,2006,20(1):39 − 41. (in Chinese with English abstract) CHEN Kaisheng, PENG Xiaoping. Applications of inclinometer in monitoring deformations of landslide[J]. Geotechnical Engineering Technique, 2006, 20（1）: 39-41. （in Chinese with English abstract）
[3] ZHAO Xin,LI Guo,ZHAO Zhifang,et al. Identifying the spatiotemporal characteristics of individual red bed landslides:A case study in western Yunnan,China[J]. Journal of Mountain Science,2022,19(6):1748 − 1766. DOI: 10.1007/s11629-022-7339-0
[4] JIN Xiaoguang, HONG Wei, ZHU Ling, et al. Study on time-space motivation and operation mechanic of landslide: A case of Zhenzilin landslide in Sichuan-Tibet highway[J]. Advanced Materials Research, 2011, 243/244/245/246/247/248/249: 2811-2818.
[5] HAI Dongjiang. Study on statistical characteristics of deep displacement of monitoring data for soil slope[J]. Environmental and Earth Sciences Research Journal,2015,2(4):11 − 16.
[6] 靳晓光,王兰生,李晓红. 滑坡滑动面位置的确定及超前预测[J]. 中国地质灾害与防治学报,2001,12(1):10 − 12. [JIN Xiaoguang,WANG Lansheng,LI Xiaohong. Determination and advanced forcasting on slide plane position for landslide[J]. The Chinese Journal of Geological Hazard and Control,2001,12(1):10 − 12. (in Chinese with English abstract) JIN Xiaoguang, WANG Lansheng, LI Xiaohong. Determination and advanced forcasting on slide plane position for landslide[J]. The Chinese Journal of Geological Hazard and Control, 2001, 12（1）: 10-12. （in Chinese with English abstract）
[7] FEARNHEAD N,MANISCALCO K,STANDING J R,et al. Deep excavations:Monitoring mechanisms of ground displacement[J]. Proceedings of the Institution of Civil Engineers - Geotechnical Engineering,2014,167(2):117 − 129. DOI: 10.1680/geng.13.00047
[8] 陈贺, 汤华, 葛修润, 等. 基于深部位移的蠕滑型滑坡预警指标及预警预报研究[J]. 岩石力学与工程学报, 2019, 38（增刊1）: 3015 − 3024 CHEN He, TANG Hua, GE Xiurun, et al. Research on early warning of creep landslide by early-warning indictors based on deep displacements[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38（Sup 1）: 3015 − 3024. （in Chinese with English abstract）
[9] 李聪,朱杰兵,汪斌,等. 滑坡不同变形阶段演化规律与变形速率预警判据研究[J]. 岩石力学与工程学报,2016,35(7):1407 − 1414. [LI Cong,ZHU Jiebing,WANG Bin,et al. Critical deformation velocity of landslides in different deformation phases[J]. Chinese Journal of Rock Mechanics and Engineering,2016,35(7):1407 − 1414. (in Chinese with English abstract) LI Cong, ZHU Jiebing, WANG Bin, et al. Critical deformation velocity of landslides in different deformation phases[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35（7）: 1407-1414. （in Chinese with English abstract）
[10] 许强,曾裕平,钱江澎,等. 一种改进的切线角及对应的滑坡预警判据[J]. 地质通报,2009,28(4):501 − 505. [XU Qiang,ZENG Yuping,QIAN Jiangpeng,et al. Study on a improved tangential angle and the corresponding landslide pre-warning criteria[J]. Geological Bulletin of China,2009,28(4):501 − 505. (in Chinese with English abstract) XU Qiang, ZENG Yuping, QIAN Jiangpeng, et al. Study on a improved tangential angle and the corresponding landslide pre-warning criteria[J]. Geological Bulletin of China, 2009, 28（4）: 501-505. （in Chinese with English abstract）
[11] 吴香根,夏阳,邢志会. 深孔位移监测技术在滑坡勘察中的应用[J]. 路基工程,2010(5):195 − 198. [WU Xianggen,XIA Yang,XING Zhihui. Application of deep hole displacement monitoring technique in landslide survey[J]. Subgrade Engineering,2010(5):195 − 198. (in Chinese with English abstract) WU Xianggen, XIA Yang, XING Zhihui. Application of deep hole displacement monitoring technique in landslide survey[J]. Subgrade Engineering, 2010（5）: 195-198. （in Chinese with English abstract）
[12] 陈云生,刘光彬,张一铭,等. 阳鹿高速公路K52新滑坡变形特征与成因机理分析[J]. 中国地质灾害与防治学报,2022,33(1):83 − 91. [CHEN Yunsheng, LIU Guangbin, ZHANG Yiming, et al. Deformation characteristics and genetic mechanism of a new landslide at K52 of Luyang freeway[J]. The Chinese Journal of Geological Hazard and Control,2022,33(1):83 − 91. (in Chinese with English abstract) CHEN Yunsheng, LIU Guangbin, ZHANG Yiming, et al. Deformation characteristics and genetic mechanism of a new landslide at K52 of Luyang freeway[J]. The Chinese Journal of Geological Hazard and Control, 2022, 33(1): 83-91.(in Chinese with English abstract)
[13] 张位华,刘勇,彭小平. 钻孔测斜成果曲线在贵州省晴隆滑坡稳定性判识中的应用[J]. 中国地质灾害与防治学报,2009,20(1):108 − 112. [ZHANG Weihua,LIU Yong,PENG Xiaoping. Application of borehole deep displacement measuring production curve in stability discrimination of Qinglong landslide[J]. The Chinese Journal of Geological Hazard and Control,2009,20(1):108 − 112. (in Chinese with English abstract) ZHANG Weihua, LIU Yong, PENG Xiaoping. Application of borehole deep displacement measuring production curve in stability discrimination of Qinglong landslide[J]. The Chinese Journal of Geological Hazard and Control, 2009, 20（1）: 108-112. （in Chinese with English abstract）
[14] 靳晓光,李晓红,王兰生,等. 滑坡深部位移曲线特征及稳定性判识[J]. 山地学报,2000,18(5):440 − 444. [JIN Xiaoguang,LI Xiaohong,WANG Lansheng,et al. Characteristics of landslide deep displacement curve and stability discriminant[J]. Journal of Mountain Science,2000,18(5):440 − 444. (in Chinese with English abstract) Jin Xiaoguang, Li Xiaohong, Wang Lansheng, et al. Characteristics of landslide deep displacement curve and stability discriminant[J]. Journal of Mountain Science, 2000, 18（5）: /span>440-444spanstyle=color: rgb（51. （in Chinese with English abstract）
[15] 胡瑞林,王珊珊. 滑坡滑面(带)的辩识[J]. 工程地质学报,2010,18(1):35 − 40. [HU Ruilin,WANG Shanshan. Main features and identification method of sliding-surfaces in soil and rock slopes[J]. Journal of Engineering Geology,2010,18(1):35 − 40. (in Chinese with English abstract) HU Ruilin, WANG Shanshan. Main features and identification method of sliding-surfaces in soil and rock slopes[J]. Journal of Engineering Geology, 2010, 18（1）: 35-40. （in Chinese with English abstract）
[16] 潘惠芳. 基于深部位移曲线形态的边坡变形特征分析[J]. 福建建筑,2019(5):54 − 61. [PAN Huifang. Analysis of slope deformation characteristics based on deep displacement curves[J]. Fujian Architecture & Construction,2019(5):54 − 61. (in Chinese with English abstract) PAN Huifang. Analysis of slope deformation characteristics based on deep displacement curves[J]. Fujian Architecture & Construction, 2019（5）: 54-61. （in Chinese with English abstract）
[17] 朱泽奇,胡琪堂,龚擎玉,等. 基于深部位移曲线特征的公路边坡稳定性评价方法研究[J]. 公路,2019,64(1):13 − 19. [ZHU Zeqi,HU Qitang,GONG Qingyu,et al. Evaluation method of highway slope stability based on deep displacement curve characteristics[J]. Highway,2019,64(1):13 − 19. (in Chinese with English abstract) ZHU Zeqi, HU Qitang, GONG Qingyu, et al. Evaluation method of highway slope stability based on deep displacement curve characteristics[J]. Highway, 2019, 64（1）: 13-19. （in Chinese with English abstract）
[18] 中国铁道科学研究院集团有限公司, 红层地区典型地质灾害失稳机理与新型防治方法技术研究[R]. 2019 China Academy of Railway Sciences, Study on instability mechanism and new prevention methods and technologies of typical geological disasters in red bed area[R]. 2019. （in Chinese））
[19] 孙志彬,杨小礼. 基于深部位移的边坡滑动特征分析[J]. 长沙理工大学学报(自然科学版),2010,7(2):43 − 47. [SUN Zhibin,YANG Xiaoli. Sliding characteristics analysis of land slide based on the deep displacement[J]. Journal of Changsha University of Science & Technology (Natural Science),2010,7(2):43 − 47. (in Chinese with English abstract) SUN Zhibin, YANG Xiaoli. Sliding characteristics analysis of land slide based on the deep displacement[J]. Journal of Changsha University of Science & Technology （Natural Science）, 2010, 7（2）: 43-47. （in Chinese with English abstract）
[20] 靳晓光. 山区公路建设中的岩土工程监测与信息化控制[D]. 成都: 成都理工大学, 2000 JIN Xiaoguang. Geotechnical engineering monitoring and information controlling in intermontane highway construction[D]. Chengdu: Chengdu University of Technology, 2000. （in Chinese with English abstract）
[21] 朱琪. 高次插值的龙格现象的测试[J]. 湖南科技学院学报,2005,26(11):206 − 208. [ZHU Qi. The runger phenomenal test of the high order interpolation[J]. Journal of Hunan University of Science and Engineering,2005,26(11):206 − 208. (in Chinese with English abstract) ZHU Qi. The Runger phenomenal test of the high order interpolation[J]. Journal of Hunan University of Science and Engineering, 2005, 26（11）: 206-208. （in Chinese with English abstract）
[22] 陈辉. 插值法在测斜数据处理中的应用[J]. 福建建设科技,2020(2):19 − 20. [CHEN Hui. Application of interpolation method in inclinometer data processing[J]. Fujian Construction Science & Technology,2020(2):19 − 20. (in Chinese with English abstract) CHEN Hui. Application of interpolation method in inclinometer data processing[J]. Fujian Construction Science & Technology, 2020（2）: 19-20. （in Chinese with English abstract）
[23] 李守定,李晓,吴疆,等. 大型基岩顺层滑坡滑带形成演化过程与模式[J]. 岩石力学与工程学报,2007,26(12):2473 − 2480. [LI Shouding,LI Xiao,WU Jiang,et al. Evolution process and pattern of sliding zone in large consequent bedding rock landslide[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(12):2473 − 2480. (in Chinese with English abstract) LI Shouding, LI Xiao, WU Jiang, et al. Evolution process and pattern of sliding zone in large consequent bedding rock landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26（12）: 2473-2480. （in Chinese with English abstract）
[24] 许强. 滑坡的变形破坏行为与内在机理[J]. 工程地质学报,2012,20(2):145 − 151. [XU Qiang. Theoretical studies on prediction of landslides using slope deformation process data[J]. Journal of Engineering Geology,2012,20(2):145 − 151. (in Chinese with English abstract) XU Qiang. Theoretical studies on prediction of landslides using slope deformation process data[J]. Journal of Engineering Geology, 2012, 20（2）: 145-151. （in Chinese with English abstract）
[25] 叶咸,高瑜,李果,等. 滑坡深部位移监测孔合位移计算与分析[J]. 公路,2020,65(10):5 − 10. [YE Xian,GAO Yu,LI Guo,et al. Calculation and analysis of combined displacement of deep displacement monitoring holes in landslide[J]. Highway,2020,65(10):5 − 10. (in Chinese with English abstract) YE Xian, GAO Yu, LI Guo, et al. Calculation and analysis of combined displacement of deep displacement monitoring holes in landslide[J]. Highway, 2020, 65（10）: 5-10. （in Chinese with English abstract）
[26] 陈贺, 李亚军, 房锐, 等. 滑坡深部位移监测新技术及预警预报研究[J]. 岩石力学与工程学报, 2015, 34（增刊2）: 4063 − 4070 CHEN He, LI Yajun, FANG Rui, et al. A novel technique for monitoring deep displacement and early-warning of landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34（Sup 2）: 4063 − 4070. （in Chinese with English abstract）
[27] 董秀军,许强,唐川,等. 滑坡位移-时间曲线特征的物理模拟试验研究[J]. 工程地质学报,2015,23(3):401 − 407. [DONG Xiujun,XU Qiang,TANG Chuan,et al. Characteristics of landslide displacement-time curve by physical simulation experiment[J]. Journal of Engineering Geology,2015,23(3):401 − 407. (in Chinese with English abstract) DONG Xiujun, XU Qiang, TANG Chuan, et al. Characteristics of landslide displacement-time curve by physical simulation experiment[J]. Journal of Engineering Geology, 2015, 23（3）: 401-407. （in Chinese with English abstract）
[28] 熊超,孙红月. 基于多因素-多尺度分析的阶跃型滑坡位移预测[J]. 吉林大学学报(地球科学版),2023,53(4):1175 − 1184. [XIONG Chao, SUN Hongyue. Step-like landslide displacement prediction based on multi-factor and multi-scale analysis[J]. Journal of Jilin University (Earth Science Edition),2023,53(4):1175 − 1184. (in Chinese with English abstract) XIONG Chao, SUN Hongyue. Step-like landslide displacement prediction based on multi-factor and multi-scale analysis[J]. Journal of Jilin University (Earth Science Edition), 2023, 53(4): 1175-1184.(in Chinese with English abstract)
[29] 顾春生,杨磊,闵望,等. 江苏常州地面沉降监测与发展趋势分析[J]. 中国地质灾害与防治学报,2023,34(2):82 − 91. [GU Chunsheng, YANG Lei, MIN Wang, et al. Monitoring and analyzing the development trend of land subsidence in Changzhou City, Jiangsu Province[J]. The Chinese Journal of Geological Hazard and Control,2023,34(2):82 − 91. (in Chinese with English abstract) GU Chunsheng, YANG Lei, MIN Wang, et al. Monitoring and analyzing the development trend of land subsidence in Changzhou City, Jiangsu Province[J]. The Chinese Journal of Geological Hazard and Control, 2023, 34(2): 82-91.(in Chinese with English abstract)
[30] 赵振宇. 基于数值计算的测斜仪监测误差分析[J]. 水文地质工程地质,2021,48(3):157 − 161. [ZHAO Zhenyu. Error analysis of an inclinometer based on numerical analysis[J]. Hydrogeology & Engineering Geology,2021,48(3):157 − 161. (in Chinese with English abstract) ZHAO Zhenyu. Error analysis of an inclinometer based on numerical analysis[J]. Hydrogeology & Engineering Geology, 2021, 48(3): 157-161.(in Chinese with English abstract)
[31] 杨志华,吴瑞安,郭长宝,等. 川西巴塘断裂带地质灾害效应与典型滑坡发育特征[J]. 中国地质,2022,49(2):355 − 368. [YANG Zhihua, WU Ruian, GUO Changbao, et al. Geo-hazard effects and typical landslide characteristics of the Batang fault zone in the western Sichuan[J]. Geology in China,2022,49(2):355 − 368. (in Chinese with English abstract) YANG Zhihua, WU Ruian, GUO Changbao, et al. Geo-hazard effects and typical landslide characteristics of the Batang fault zone in the western Sichuan[J]. Geology in China, 2022, 49(2): 355-368.(in Chinese with English abstract)
[32] HERRERA G,FERNÁNDEZ-MERODO J A,MULAS J,et al. A landslide forecasting model using ground based SAR data:The Portalet case study[J]. Engineering Geology,2009,105(3/4):220 − 230.
[33] N D ROSE,O HUNGR. Forecasting potential rock slope failure in open pit minesusing the inverse-velocity method[J]. International Journal of Rock Mechanics and Mining Sciences,2007,44:308 − 320. DOI: 10.1016/j.ijrmms.2006.07.014
[34] 朱赛楠,魏英娟,王平,等. 大型单斜层状基岩滑坡变形特征与失稳机制研究—以重庆石柱县龙井滑坡为例[J]. 岩石力学与工程学报,2021,40(4):739 − 750. [ZHU Sainan,WEI Yingjuan,WANG Ping,et al. Research on deformation characteristics and instability mechanisms of large monoclinal layered bedrock landslides:A case study of the Longjing landslide in Shizhu County,Chongqing[J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(4):739 − 750. (in Chinese with English abstract) ZHU Sainan, WEI Yingjuan, WANG Ping, et al. Research on deformation characteristics and instability mechanisms of large monoclinal layered bedrock landslides: a case study of the Longjing landslide in Shizhu County, Chongqing[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40（4）: 739-750. （in Chinese with English abstract）
[35] 黄秋香, 汪家林, 邓建辉. 基于多点位移计监测成果的坡体变形特征分析[J]. 岩石力学与工程学报, 2009, 28（增刊1）: 2667 − 2673 HUANG Qiuxiang, WANG Jialin, DENG Jianhui. Slope deformation character analysis based on monitoring results of multiple multi-point borehole extensometer[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28（Sup 1）: 2667 − 2673. （in Chinese with English abstract）
[36] CROSTA G B,AGLIARDI F. How to obtain alert velocity thresholds for large rockslides[J]. Physics and Chemistry of the Earth,Parts A/B/C,2002,27(36):1557 − 1565. DOI: 10.1016/S1474-7065(02)00177-8
[37] 焦龙进,李磊,姜德民. 滑坡勘查中滑动面判定方法分析[J]. 建筑技术开发,2019,46(11):134 − 135. [JIAO Longjin,LI Lei,JIANG Demin. Simple analysis of sliding surface determination method in landslide exploration[J]. Building Technology Development,2019,46(11):134 − 135. (in Chinese with English abstract) JIAO Longjin, LI Lei, JIANG Demin. Simple analysis of sliding surface determination method in landslide exploration[J]. Building Technology Development, 2019, 46（11）: 134-135. （in Chinese with English abstract）
[38] VAN ASCH T W J,VAN BEEK L P H,BOGAARD T A. Problems in predicting the mobility of slow-moving landslides[J]. Engineering Geology,2007,91(1):46 − 55. DOI: 10.1016/j.enggeo.2006.12.012
[39] HE Chuncan,HU Xinli,TANNANT D D,et al. Response of a landslide to reservoir impoundment in model tests[J]. Engineering Geology,2018,247:84 − 93. DOI: 10.1016/j.enggeo.2018.10.021
[40] SONG Jian,FAN Qingqing,FENG Tugen,et al. A multi-block sliding approach to calculate the permanent seismic displacement of slopes[J]. Engineering Geology,2019,255:48 − 58. DOI: 10.1016/j.enggeo.2019.04.012
[41] STEAD D,WOLTER A. A critical review of rock slope failure mechanisms:the importance of structural geology[J]. Journal of Structural Geology,2015,74:1 − 23. DOI: 10.1016/j.jsg.2015.02.002
[42] HUNGR O,LEROUEIL S,PICARELLI L. The Varnes classification of landslide types,an update[J]. Landslides,2014,11(2):167 − 194. DOI: 10.1007/s10346-013-0436-y
[43] ZHANG Shilin,ZHU Zhaohui,QI Shunchao,et al. Deformation process and mechanism analyses for a planar sliding in the Mayanpo massive bedding rock slope at the Xiangjiaba Hydropower Station[J]. Landslides,2018,15(10):2061 − 2073. DOI: 10.1007/s10346-018-1041-x
[44] ZHAN Liangtong,GUO Xiaogang,SUN Qianqian,et al. The 2015 Shenzhen catastrophic landslide in a construction waste dump:analyses of undrained strength and slope stability[J]. Acta Geotechnica,2021,16(4):1247 − 1263. DOI: 10.1007/s11440-020-01083-8
-
期刊类型引用(6)
1. 王勇，邢振涛，李锁，闫勇，司甜. 基于SBAS-InSAR和光学遥感的天津市北部山区潜在滑坡识别研究. 灾害学. 2025(01): 30-35 . 
百度学术
2. 谢哲，侯照方，谢杰. 基于钻探及室内试验的蒙城县地面沉降量预测. 能源技术与管理. 2025(01): 24-26 . 百度学术
3. 赵志远，葛超英，徐雯佳. 时序InSAR技术对淮扬区域地面沉降监测. 四川地质学报. 2025(01): 162-169 . 百度学术
4. 李幸丽，戴华阳，方军，张豪磊. 基于SBAS-InSAR技术的老采空区注浆充填地表变形时空分布特征分析. 中国矿业. 2024(11): 86-94 . 百度学术
5. 马恩华，李益敏，俞文轩，吕圣彬. 基于InSAR的玉溪市红塔区地面沉降时空分布特征. 人民长江. 2024(S2): 113-120 . 百度学术
6. 李松虎. 亳州市地下水超采现状及存在问题分析. 治淮. 2023(11): 7-9 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 2049
- HTML全文浏览量: 657
- PDF下载量: 187
- 被引次数: 7
邮件订阅
RSS