Evaluation methods for performance of post-construction settlement prediction models in thick loess filled ground
-
摘要: 工后沉降预测结果是黄土高填方场地变形稳定性评价和建筑物规划布局的重要参考依据。为遴选适合黄土高填方场地的工后沉降预测模型,基于某典型黄土高填方工程的实测沉降数据,分析了工后沉降曲线的变化规律和发展趋势,建立了17种回归参数模型,提出了模型预测效果的评价指标和方法。结果表明:(1)该工程填方区工后沉降历时曲线呈“缓变型”变化,土方填筑完工初期无陡增段,随时间增加沉降速率逐步降低,尚未出现沉降趋于稳定的水平段;(2)将外推预测误差、内拟合误差和后验误差比最小化作为综合控制目标,可遴选出理想的回归参数模型;(3)MMF模型(Ⅱ型)和双曲线模型具有较高的预测精度、较好的稳定性和较强的适应性,在17种模型中的预测效果最佳;(4)沉降数据的变化越平稳,模型预测效果越好;(5)增大建模数据的时间跨度,会提升预测精度,但增大至一定值后,预测精度提升效果不再显著。Abstract: The prediction of post-construction settlement is an important reference for the evaluation of deformation stability evaluation and building layout planning in thick loess filled ground. To choose suitable models for predicting post-construction settlement in thick loess filled grounds, the characteristics of post-construction settlement curves are analyzed based on the measured settlement of a thick loess fill ground project. Seventeen regression parameter models are established, and some evaluation indexes and methods for models are proposed. The best prediction models for post-construction settlement prediction are optimized. The results indicate that the post-construction settlement curves of the filling area change slowly, with no steep increase in the initial stage of earthwork filling. The settlement rate gradually decreases with time, and there is no horizontal section where the settlement tends to be stable. The optimal regression parameter model can be selected by minimizing the extrapolation prediction error, the internal fitting error, and the posteriori error ratio as the comprehensive control objective. The MMF model (TypeⅡ) and hyperbolic model show high prediction accuracy, good stability, and strong adaptability, with the prediction effect being the best among the 17 models. The more stable the settlement data changes, the better the model prediction effect. Increasing the time span of modeling data would improve the prediction accuracy, but the improvement effect on prediction accuracy would no longer be significant after reaching a certain value.
-
Keywords:
- loess /
- thick loess fill ground /
- post-construction settlement /
- prediction model /
- evaluation index
-
0. 引言
我国黄土丘陵沟壑区分布广,显著特点是地形起伏、沟壑纵横、平地较少。随着西部经济社会的快速发展,对工程建设用地的需求也越来越大,为了增加建设用地,多利用城市周边的低丘缓坡,采取“削峁填沟”方式造地,由此出现了越来越多的黄土高填方工程,这些工程涉及城市建设用地[1]、机场建设用地[2]和工业建设用地[3]等众多工程领域。由于黄土高填方场地跨越复杂的地形和地质单元,具有挖填交替、方量巨大、填料性质特殊、承受多场耦合作用和工程环境恶劣等特点,加之填方厚度大幅度变化、沟底原地基土的性质差异大、填筑体中水分长时间迁移变化等原因,会发生长时间的工后沉降。当土方填筑完成进入工后建设阶段,为了确定合理开工时间起点,避免因地基沉降过大造成建筑物开裂、倾斜、下沉过大等工程事故,必须科学准确预测和评估场地的工后沉降变形情况。
现有的沉降预测方法主要分为两大类[4-5]:第一类是依据固结理论、本构模型的理论方法;第二类是基于实测沉降资料推算沉降量与时间关系的经验方法。理论方法的物理力学意义明确,但受模型简化假定、参数测定及取值等因素影响大,沉降计算值往往与实测值相差较大,现阶段尚难以完全满足工程需求。相比而言,第二类经验方法是以实测沉降资料为依据,能够较为简便、快捷地推算后期沉降(包括最终沉降),如各类神经网络模型和回归参数模型等[6-8],已被广泛应用于各类工程。现有文献中关于沉降预测的经验模型有数十种,如何定量地评价模型的预测效果,从众多模型中筛选出比较可靠的模型,从而获得更加准确的预测结果,就显得尤为重要。以往由于建模数据样本选择缺陷以及预测效果定量化评价指标和方法不足,在实际工程中,一些工程技术人员在进行沉降预测时,常将已知的所有实测数据用于识别和估计模型参数,仅考虑内拟合效果,而忽视外推预测效果,实际应用时出现了内拟合效果好,但外推预测效果差的情况,容易造成对模型实际预测能力的误导性判断。究竟如何来评价经验模型的预测效果,哪些经验模型适合黄土高填方场地的工后沉降预测,国内外尚未有系统全面的总结和梳理。
本文根据陕北某沟谷地形中黄土高填方场地的工后沉降实测数据,在分析工后沉降曲线特征的基础上,建立了17种常用的回归参数模型,并给出了模型预测效果评价的建议模式,从中遴选出适合黄土高填方场地工后沉降预测的数学模型,相关成果可为西北地区类似黄土高填方工程的工后沉降预测提供参考与借鉴。
1. 典型工后沉降曲线特征
陕北某黄土高填方工程地处黄土丘陵沟壑区,原始场地内大小冲沟发育,地形破碎,呈现梁峁起伏,沟谷深切的特殊地形。梁峁区的主要地层自上而下为上更新统马兰黄土、中更新统离石黄土、新近系棕红色黏土、侏罗系砂岩及泥岩互层。冲沟区除可见梁峁区厚度有所不同的所有地层之外,还分布有第四系全新统地层,地质成因主要是冲洪积、淤积、崩积和滑坡堆积。沟谷原地基采用强夯法处理,填筑体主要采用分层碾压法+强夯补强处理,填料为挖填交接线以上土层,主要为
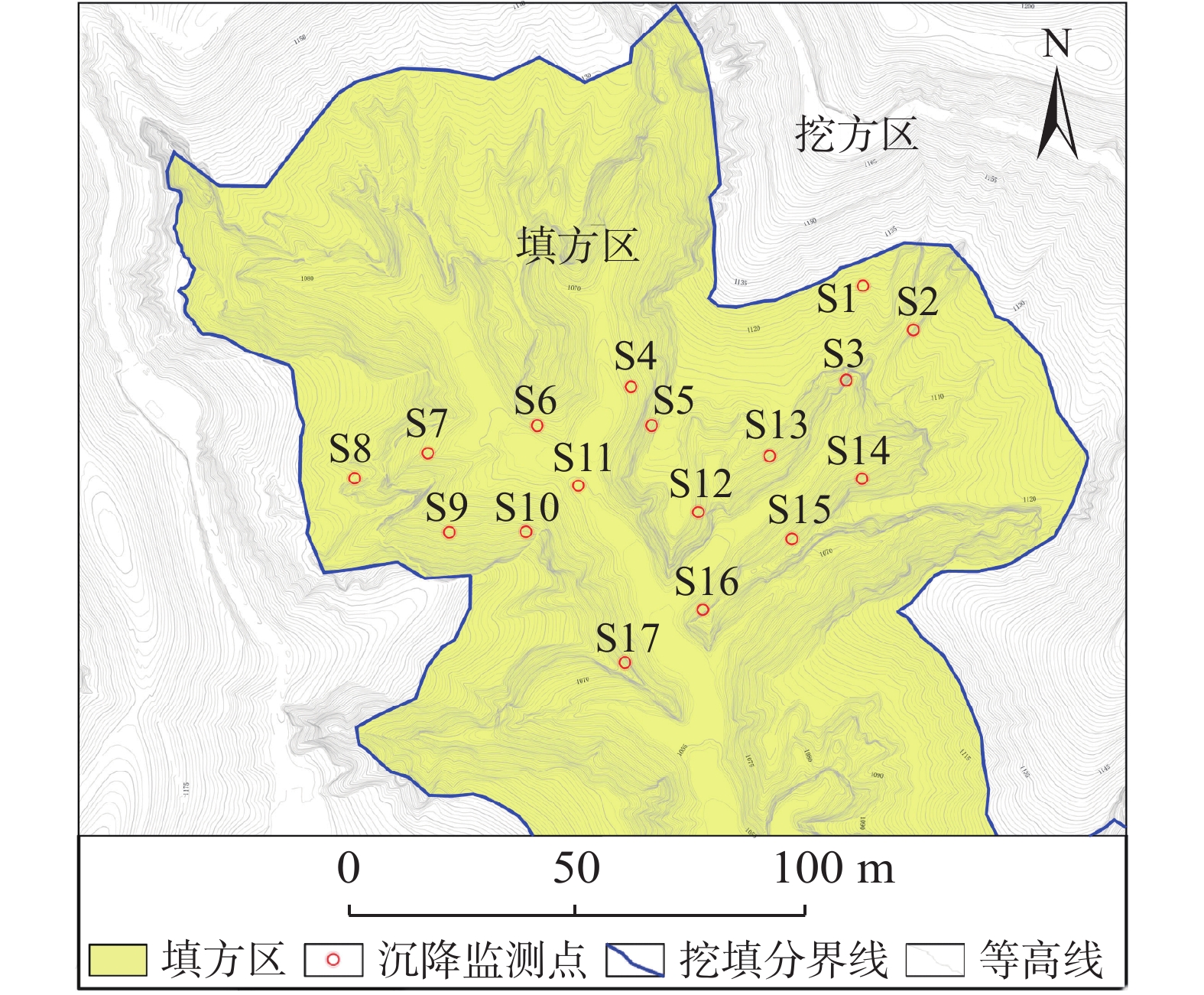
${\rm{Q}p}^{{{{eol+el}}}}$ 黄土及古土壤,填土的压实系数要求不小于0.93(最大干密度与最优含水率采用重型击实试验确定)。工程东北部试验场地内代表性地表沉降监测点的布置情况如图1所示。各监测点的工后沉降历时曲线如图2所示。监测点均位于填方区,填土厚度范围为2~52 m,相邻监测点的间距为50~100 m。工后沉降监测工作自土方填筑完成后开始,截至2019年12月13日,累积观测历时395 d。
由图2可知,该场地填方区的工后沉降曲线属于“缓变型”变化,随观测时长的增加,沉降曲线逐步趋向于平缓,尚未出现趋于稳定的水平段也并未出现明显的拐点。在历时395 d时,沉降量最大的监测点S12,沉降速率已由最初的0.41 mm/d降低至0.10 mm/d;沉降量最小的监测点S8,沉降速率已由最初的0.13 mm/d降低至0.01 mm/d;临近挖填交界线附近的监测点S1还发生了微小的回弹变形。土方建筑完成后,填土自重荷载不增加,原地基上覆荷载不变,沉降曲线在观测初期均无明显的陡增段,表明瞬时沉降已经完成,结合文献[9]的固结试验结果可知,此时主固结沉降尚未完成,土体的蠕变也伴随发生,沉降量还将继续增加,但沉降速率递减,这与土方分层慢速填筑、填土非饱和的特征相吻合。
2. 工后沉降预测的回归参数模型
回归参数模型是根据沉降曲线特征,选择与其相适应的数学模型,再对未来某时刻的沉降(包括最终沉降)进行预测。本文梳理出了17种常用回归参数模型,函数表达式如表1所示,其中:t为时间;t0为初始时间;
${\hat s_t}$ 为t时的沉降量;${\hat s'_t}$ 为t时的沉降速率;a、b、c、d为模型参数;e为自然常数。根据曲线形态特点,将表1中所列模型分为以下两类:①第Ⅰ类模型为“S”型曲线模型,主要包括:Logistic模型[10-11]、Gompertz模型[12-13]、Usher模型[14]、Weibull模型[15-16]、Morgan-Mercer-Flodin模型(简称MMF模型,包括Ⅰ型和Ⅱ型)[17]、Richards模型[18-19]、Knothe模型(包括Ⅰ型和Ⅱ型)[20-21]、Bertalanffy模型[22-23]、邓英尔模型[24];②第Ⅱ类模型为“J”型曲线模型,主要包括:Spillman模型[25]、指数曲线模型[26-28]、双曲线模型[29-30]、幂函数模型[31]、平方根函数模型[31]、对数函数模型[31]、对数抛物线模型[31]、星野法[32]。表1所列模型分为收敛模型和发散模型两种,其中收敛模型可直接预测最终沉降量,发散模型以达到某一较小沉降速率时(如参考现行《建筑变形测量规范》[33],取沉降速率小于0.01~0.04 mm/d作为稳定标准)的沉降量作为最终沉降量。表 1 沉降预测中常用的回归参数预测模型Table 1. Summary of regression parameter prediction models for settlement prediction类型 模型名称 数学表达式 沉降速率 备 注 第
Ⅰ
类
模
型Logistic ${\hat s_t} = a/(1 + b{{\text{e}}^{ - ct}})$ ${\hat s'_t} = abc{{\text{e}}^{ - ct}}/{(1 + b{{\text{e}}^{ - ct}})^2}$ 收敛模型 Gompertz ${\hat s_t} = a{{\text{e}}^{ - {{\text{e}}^{b - ct}}}}$ ${\hat s'_t} = ac{{\text{e}}^{ - {{\text{e}}^{b - ct}}}}{{\text{e}}^{b - ct}}$ 收敛模型 Usher ${\hat s_t} = a/{(1 + b{{\text{e}}^{ - ct}})^d}$ ${\hat s'_t} = abcd{{\text{e}}^{ - ct}}{(1 + b{{\text{e}}^{ - ct}})^{ - 1 - d}}$ 收敛模型 Weibull ${\hat s_t} = a(1 - b{{\text{e}}^{ - c{t^d}}})$ ${\hat s'_t} = abcd{{\text{e}}^{ - c{t^d}}}{t^{ - 1 + d}}$ 收敛模型 MMF-Ⅰ ${\hat s_t} = (ab + c{t^d})/(b + {t^d})$ ${\hat s'_t} = cd{t^{d - 1}}/(b + {t^d}) - d{t^{d - 1}} \cdot (ab + c{t^d})/{(b + {t^d})^2}$ 收敛模型 MMF-Ⅱ ${\hat s_t} = a{t^b}/(c + {t^b})$ ${\hat s'_t} = ab{t^{b - 1}}/(c + {t^b}) - ab{t^{2b - 1}}/{(c + {t^b})^2}$ 收敛模型 Richards ${\hat s_t} = a{(1 - b{{\text{e}}^{ - ct}})^{1/(1 - d)}}$ ${\hat s'_t} = abc{{\text{e}}^{ - ct}}{(1 - b{{\text{e}}^{ - ct}})^{d/(1 - d)}}/(1 - d)$ 收敛模型 Knothe-Ⅰ ${\hat s_t} = a{(1 - {{\text{e}}^{ - b{t^c}}})^d}$ ${\hat s'_t} = abcd{t^{c - 1}}{{\text{e}}^{ - b{t^c}}} \cdot {(1 - {{\text{e}}^{ - b{t^c}}})^{d - 1}}$ 收敛模型 Knothe-Ⅱ ${\hat s_t} = a{(1 - {{\text{e}}^{ - bt}})^c}$ ${\hat s'_t} = abc{{\text{e}}^{ - bt}}{(1 - {{\text{e}}^{ - bt}})^{c - 1}}$ 收敛模型 Bertalanffy ${\hat s_t} = {[{a^{1/3}} - {(a - b)^{1/3}} \cdot {{\text{e}}^{ - ct}}]^3}$ ${\hat s'_t} = 3{(a - b)^{1/3}}c{{\text{e}}^{ - ct}} \cdot {[{a^{1/3}} - {(a - b)^{1/3}} \cdot {{\text{e}}^{ - ct}}]^2}$ 收敛模型 邓英尔 ${\hat s_t} = a/(1 + b{{\text{e}}^{ - c{t^d}}})$ ${\hat s'_t} = abcd{{\text{e}}^{ - c{t^d}}}{t^{d - 1}}/{(1 + b{{\text{e}}^{ - c{t^d}}})^2}$ 收敛模型 第
Ⅱ
类
模
型Spillman ${\hat s_t} = a - (a - b){{\text{e}}^{ - ct}}$ ${\hat s'_t} = (a - b)c{{\text{e}}^{ - ct}}$ 收敛模型 指数曲线 ${\hat s_t} = a(1 - {{\text{e}}^{ - bt}})$ ${\hat s'_t} = ab{{\text{e}}^{ - bt}}$ 收敛模型 双曲线 ${\hat s_t} = t/(a + bt)$ ${\hat s'_t} = a/{(a + bt)^2}$ 收敛模型 幂函数 ${\hat s_t} = a{t^b}$ ${\hat s'_t} = ab{t^{b - 1}}$ 发散模型 平方根函数 ${\hat s_t} = a + b\sqrt t $ ${\hat s'_t} = b/2\sqrt t $ 发散模型 对数函数 ${\hat s_t} = a\ln t + b$ ${\hat s'_t} = a/t$ 发散模型 对数抛物线 ${\hat s_t} = a{(\lg t)^2} + b\lg t + c$ ${\hat s'_t} = \lg {\text{e}} \cdot (b + 2a\lg t) \cdot {t^{ - 1}}$ 发散模型 星野法 ${\hat s_t} = {s_0} + \dfrac{ {ab\sqrt {t - {t_0} } } }{ {\sqrt {1 + {b^2}\left( {t - {t_0} } \right)} } }$ ${\hat s'_t} = \dfrac{ {ab} }{ {2\sqrt {[1 + {b^2}(t - {t_0})](t - {t_0})} } } - \dfrac{ {a{b^3}\sqrt {t - {t_0} } } }{ {2{ {[1 + {b^2}(t - {t_0})]}^{3/2} } } }$ 收敛模型 3. 模型预测效果的评价方法
评价一个模型的预测效果,不但要看模型对已有实测数据的吻合程度,更要看模型的外推预测性能。若建模数据和检验数据均采用同一组数据,则仅能评价模型的内拟合效果,无法评估模型的外推预测效果。因此,应将已有实测沉降数据(n期)分为前后两部分,前一部分数据(m期,m<n)用来建模,后一部分数据(n−m期)用来检验模型的外推预测效果。根据前一部分数据获得模型的内拟合误差,后一部分数据获得模型的外推预测误差,其中前者为内误差,后者为外误差。
3.1 模型的内拟合效果评价指标
模型内拟合效果的评价采用决定系数(R2)、误差平方和(SSE)、均方根误差(RMSE)三个指标:
$$ R^{2}=1-\sum_{i=1}^{m}\left(s_{t_{i}}-s_{t_{i}}^{*}\right) / \sum_{i=1}^{m}\left(s_{t_{i}}-\frac{1}{m} \sum_{i=1}^{m} s_{t_{i}}^{*}\right)^{2} $$ (1) $$ S S E=\sum_{i=1}^{m}\left(s_{t_{i}}-s_{t_{i}}^{*}\right)^{2} $$ (2) $$ R M S E=\sqrt{\frac{1}{m} \sum_{i=1}^{m}\left(s_{t_{i}}-s_{t_{i}}^{*}\right)^{2}} $$ (3) 式(1)—(3)中,
${t_i}$ 为第 i 期数据对应的时间;${s_{{t_i}}}$ 为第 i 期的实测值($i =1,2,\cdots,m $ );$s_{{t_i}}^*$ 为第 i 期的内拟合值($i =1,2,\cdots,m $ )。上述评价指标中,R2能反映曲线拟合效果的好坏,其值越接近于1,则实测数据通过模型的解释性就越强;SSE、RMSE值能反映拟合值偏离实测值的程度,数值越接近于0,表示拟合效果越好。根据式(1)—(3)所列指标评价各模型对建模数据的解释程度,从中遴选出拟合值偏离实测值小、拟合优度高的模型。
3.2 模型的外推预测效果评价指标
模型外推预测效果的评价采用绝对误差(∆e)、相对误差(δ)、平均绝对百分比误差(MAPE)、平均绝对误差(MAD)、均平方误差(MSE)、平均预测误差(MFE)六个指标,计算公式如下:
$$ \Delta e=s_{t_{i}}-\hat{s}_{t_{i}}^{*} $$ (4) $$ \delta=\frac{\Delta e}{s_{t_{i}}}=\frac{s_{t_{i}}-\hat{s}_{t_{i}}^{*}}{s_{t_{i}}} \times 100 \% $$ (5) $$ { MAPE }=\frac{1}{n-m} \sum_{i=m+1}^{n} \frac{\left|s_{t_{i}}-\hat{s}_{t_{i}}^{*}\right|}{s_{t_{i}}} \times 100 \% $$ (6) $$ M A D=\frac{1}{n-m} \sum_{i=m+1}^{n}\left|s_{t_{i}}-\hat{s}_{t_{i}}^{*}\right| $$ (7) $$ M S E=\frac{1}{n-m} \sum_{i=m+1}^{n}\left(s_{t_{i}}-\hat{s}_{t_{i}}^{*}\right)^{2} $$ (8) $$ M F E=\frac{1}{n-m} \sum_{i=m+1}^{n}\left(s_{t_{i}}-\hat{s}_{t_{t}}^{*}\right) $$ (9) 式(4)—(9)中,
${s_{{t_i}}}$ 为第 i 期的实测值($i=m+1,m+ 2, \cdots , n$ );$\hat s_{{t_i}}^{\text{*}}$ 为第 i 期的外推预测值($i=m+1,m+2, \cdots , n$ )。△e、δ能反映某一期预测值偏离实测值的程度;MAPE为相对指标,能较好地反映总体预测精度,其值越小越好,极限为0,一般当MAPE<10%时,认为是较好的预测模型[34];MAD、MSE为绝对指标,能较好地反映模型的总体预测精度,但无法衡量无偏性;MFE能较好地衡量预测模型的无偏性,但无法反映预测值偏离实测值的程度,其值越接近于0,则模型越是无偏,预测效果也越好。考虑到上述评价指标各有侧重,故将上述指标结合起来作为模型外推预测效果的综合评价指标。3.3 模型预测效果的内外误差关系评价指标
回归参数模型属于参数定常的静态预测模型,实际应用时常会出现内拟合误差较小,但外推预测误差较大的情况。因此,在评价模型预测效果时,既要考虑内拟合误差,也要考虑外推预测误差,后者比前者更能反映模型在外推时的预测效果。本文采用式(10)建立外推预测误差指标Mi与内拟合误差指标
$M_i^*$ 之间的联系,这里称之为模型的“后验误差比Ci”,该值反映了模型外推预测误差相对于内拟合误差的变化情况。$$ C_i=M_i/M_i^* $$ (10) 式(10)中,Mi、
$M_i^*$ 为同一种误差评价指标,考虑到计算内拟合误差和外推预测误差所用实测数据量可能不同,Mi、$M_i^*$ 值不宜采用绝对指标,而应采用相对指标,故采用平均绝对百分比误差值来进行计算,即:$$ C_i=\frac{M_i}{M_i^*}=\frac{MAPE}{MAPE^{*}} $$ (11) 式中,
${MAPE^{*}} $ 表示内拟合值的平均绝对百分比误差值。当采用式(6)计算内拟合误差的MAPE值时,将预测值
$\hat s_{{t_i}}^{\text{*}}$ 采用内拟合值$s_{{t_i}}^*$ 替换。当建模数据和检验数据一定时,在某一外推预测时段内,若Ci>1则表明外推预测误差相对内拟合误差在增大;若Ci<1则表明外推预测误差相对于内拟合误差在减小。3.4 模型预测效果评价指标的使用建议
当对比不同模型对同一监测点沉降数据的外推预测效果,检验模型的稳定性时,建议采用MAPE、MAD、MSE,结合Ci及MFE作为评价指标。当评价同一模型对不同监测点沉降数据的预测效果,检验模型的适应性时,考虑到不同监测点沉降数据的量级可能存在较大差别,若采用绝对指标MAD、MSE不利于模型预测效果的定量化和规范化比较,故建议采用相对指标MAPE结合MFE及Ci作为评价指标。同理,当不同模型对同一监测点沉降数据的内拟合效果评价时,建议采用R2、SSE、RMSE作为评价指标;当评价同一模型对不同监测点沉降数据的内拟合效果时,建议采用相对指标R2。
4. 模型预测效果的工程实例分析
4.1 回归参数模型预测效果的对比分析
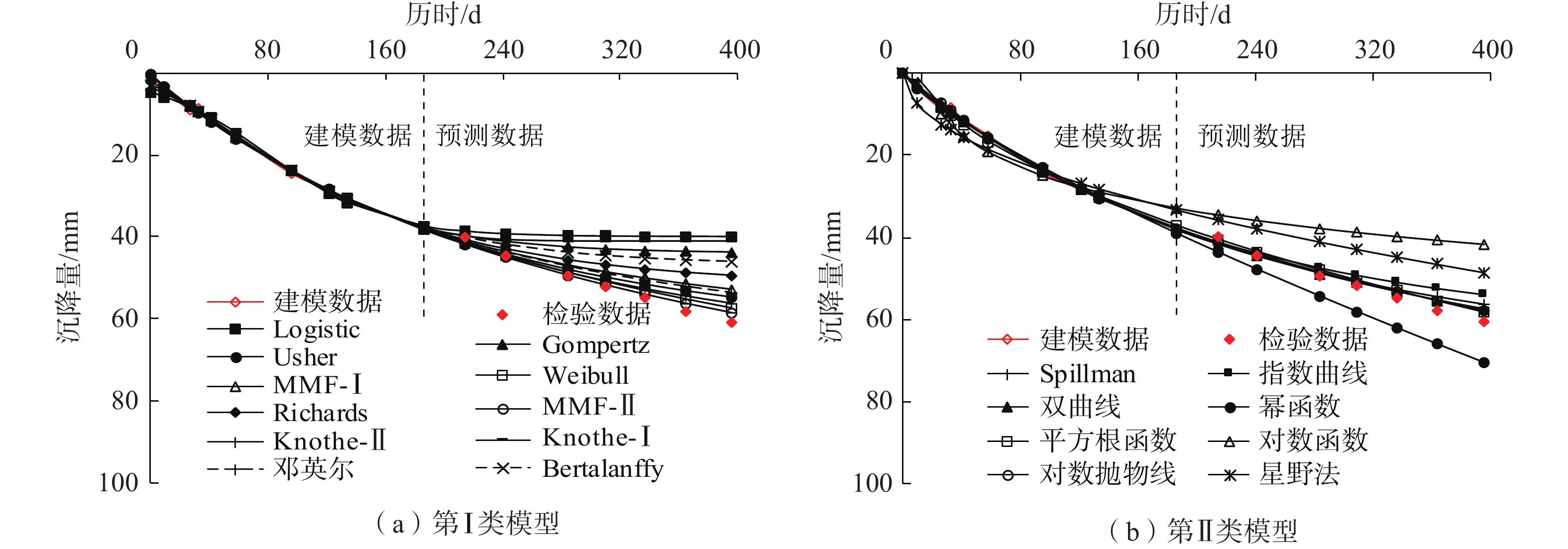
本次以试验场地内的监测点S6为例,对各模型的预测效果进行对比分析。该监测点处的填土厚度约52 m,观测历时395 d,共有17期实测数据。采用表1中所列回归参数模型,利用前10期(0~186 d)实测数据求解模型参数,后7期(214~395 d)实测数据检验模型的外推预测效果,外推预测数据时长与总数据时长之比为0.54。各模型的内拟合及外推预测曲线如图3所示,对应内拟合及外推预测误差曲线如图4所示。各模型对监测点S6实测数据的内拟合及外推预测结果如表2所示。
表 2 各模型对典型监测点S6实测数据的内拟合及外推预测结果Table 2. Internal-fitting and extrapolation prediction results of each model for the measured settlement data at a typical monitoring point S6类型 模型名称 模型参数 内拟合效果 外推预测效果 后验误差
比Cia b c d MAPE* /% SSE RMSE R2 MAPE /% MAD MSE MFE 第
Ⅰ
类
模
型Logistic 39.7540 7.6080 0.0252 — 9.88 8.06 0.95 0.9928 21.66 11.77 179.32 11.77 2.19 Gompertz 43.7854 0.9395 0.0150 — 6.10 3.09 0.59 0.9973 16.39 8.99 111.11 8.99 2.69 Usher 64.0873 −0.9931 0.0049 −1.0149 5.16 2.72 0.52 0.9981 5.03 2.74 10.97 2.31 0.98 Weibull 3.3377 −52.2248 14.7577 −0.4232 3.58 2.04 0.45 0.9986 3.09 1.65 3.87 1.21 0.86 MMF-Ⅰ 2.4888 869.7498 68.8715 1.3199 3.26 1.71 0.44 0.9985 7.18 3.93 21.54 3.62 2.20 MMF-Ⅱ 113.9160 0.9777 329.4676 — 5.84 3.04 0.55 0.9979 2.05 1.05 1.77 0.41 0.35 Richards 51.8874 0.8687 0.0085 0.3724 3.18 1.66 0.43 0.9985 9.98 5.49 42.78 5.25 3.13 Knothe-Ⅰ 41.0949 0.0000 4.0687 0.2098 4.49 2.17 0.49 0.9981 18.75 10.31 147.80 10.31 4.18 Knothe-Ⅱ 68.6817 240.2071 0.9562 — 5.65 2.87 0.56 0.9975 3.79 2.05 6.41 1.58 0.67 Bertalanffy 46.8972 36.1948 0.0116 — 4.45 2.03 0.47 0.9982 13.42 7.39 76.86 7.32 3.02 邓英尔 3.2623 −0.9558 28.7664 −1.2368 3.24 1.81 0.42 0.9987 6.32 3.45 16.62 3.11 1.95 第
Ⅱ
类
模
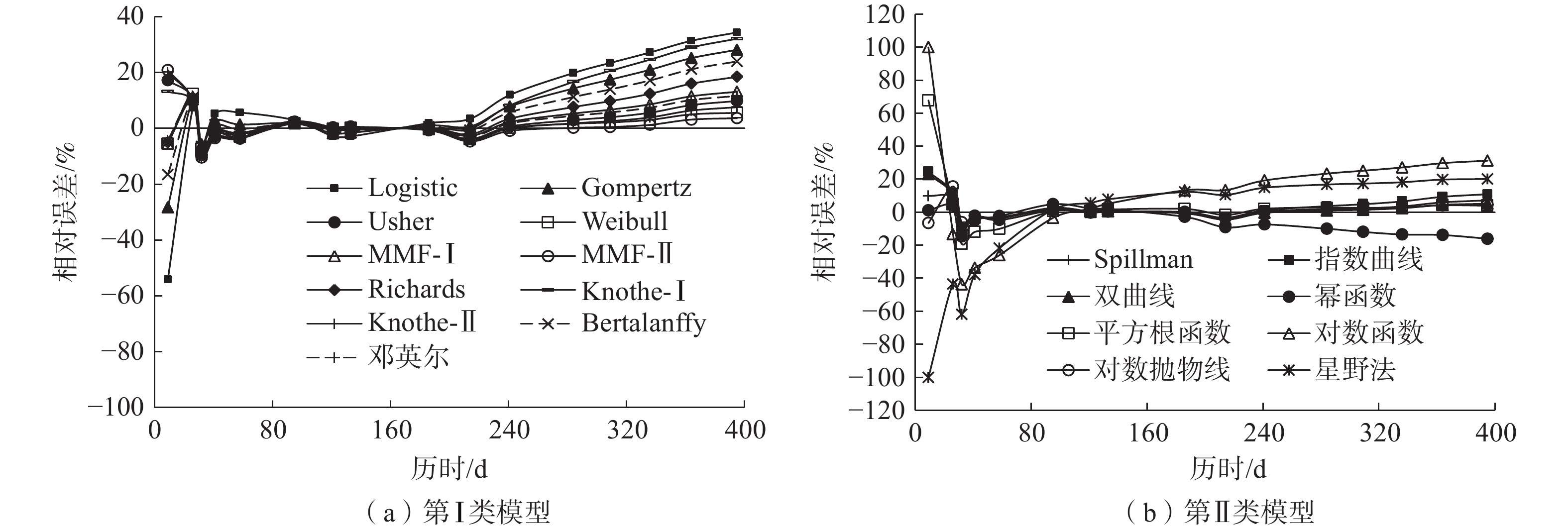
型Spillman 68.5727 0.7074 0.0043 — 4.50 2.47 0.52 0.9978 3.59 1.93 5.67 1.38 0.80 指数曲线 62.6226 0.0050 — — 5.95 3.01 0.58 0.9973 5.71 3.12 13.95 2.74 0.96 双曲线 3.1221 0.0095 — — 6.00 3.06 0.55 0.9979 2.75 1.46 3.16 0.93 0.46 幂函数 0.6425 0.7852 — — 4.34 5.38 0.73 0.9963 11.67 6.15 42.57 -6.15 2.69 平方根函数 −8.9505 3.3748 — — 13.18 14.00 1.25 0.9876 2.90 1.54 2.78 1.36 0.22 对数函数 11.6931 −28.2990 — — 26.75 113.31 3.55 0.8993 24.20 12.77 182.58 12.77 0.90 对数抛物线 21.4982 −43.5385 25.8604 — 4.12 2.83 0.56 0.9975 2.75 1.46 2.83 1.07 0.67 星野法 1367.0000 0.0018 — — 32.50 114.39 3.38 0.9205 16.81 8.80 84.05 8.80 0.52 注:“—”表示无此参数。 由图3、图4可知,两类模型的外推预测误差均随着预测时长的增加而增大,第Ⅰ类模型的预测值较实测值总体偏小,第Ⅱ类模型中除幂函数模型的预测值较实测值总体偏大外,其余模型的预测值较实测值总体偏小。第Ⅰ类模型为“S”型曲线模型,该类模型具有初期增长缓慢、前期增长较快、中期增长放缓,后期趋于平稳的特征,实测沉降曲线与该类模型的中期、后期曲线形态相似,与其初期、前期不同,这导致模型在初期、前期的拟合值与实测值相差较大,但随观测时长的增加,拟合曲线与实测曲线逐渐吻合,内拟合误差总体呈逐步降低趋势。第Ⅱ类模型为“J”型曲线模型,该类模型的曲线增长逐步放缓,内拟合误差总体呈先减小后增大的趋势。
由表2可知,MAPE、MAD、MSE对模型外推预测效果的评价结果具有较好的一致性。对MAPE值小于10%的模型,按照预测误差由小到大排序如下:①第Ⅰ类模型:MMF-Ⅱ、Weibull、Knothe-Ⅱ、Usher、邓英尔、MMF-Ⅰ、Richards;②第Ⅱ类模型:双曲线、对数抛物线、平方根函数、Spillman、指数曲线。由排序可知,MMF-Ⅱ模型和双曲线模型分别代表了两类模型中总体预测效果最好的模型,其中MMF-Ⅱ模型对各单期沉降的预测误差范围为:
$\Delta e$ =−1.7~3.1 mm,$ \delta $ =−4.3%~5.2%;双曲线模型对各单期沉降的预测误差范围为:$\Delta e$ =−1.9~2.2 mm,$ \delta $ =−4.7%~3.7%。由表2可知,SSE、RMSE、R2对模型内拟合效果的评价也具有较好的一致性。虽然绝大多数模型的R2值均超过0.99,具有较高的拟合优度,但这些模型的外推预测误差相差较大,表明内拟合误差指标不能代替外推预测误差指标作为模型选择和评价的唯一标准。综上可知,MMF-Ⅱ模型和双曲线模型的平均绝对百分比误差MAPE<3%、平均预测误差MFE<1、决定系数R2>0.99,后验误差比Ci<1,能较准确地反映黄土高填方场地工后沉降的变化规律和发展趋势。4.2 优选模型对不同沉降数据的适应性检验
试验场地中监测点S1~S17的工后沉降观测时间相同,其中S1主要为回弹变形,不符合前述优选模型所代表的曲线形态特征。为了检验优选模型对不同沉降数据的适应性,本次对除S1外其它监测点S2—S17统一采用前10期(0~186 d)实测数据建模,后7期(214~395 d)实测数据检验模型的外推预测效果。优选模型对监测点S2—S17的内拟合和外推预测结果如表3所示。
表 3 优选模型对不同监测点沉降数据的内拟合和外推预测结果Table 3. Internal-fitting and extrapolation prediction of settlement data for different monitoring points using the optimal model监测点 模型名称 模型参数 内拟合效果
R2外推预测效果 后验误差比
Cia b c MAPE /% MFE S2 双曲线 15.8265 0.0747 — 0.9805 8.33 −0.60 0.58 MMF-Ⅱ 7.4942 1.5515 829.1400 0.9880 7.42 0.56 0.55 S3 双曲线 4.9610 0.0145 — 0.9969 3.28 1.31 0.73 MMF-Ⅱ 64.7724 1.0199 344.1345 0.9969 4.11 1.60 0.88 S4 双曲线 3.4475 0.0099 — 0.9973 0.78 0.56 0.12 MMF-Ⅱ 90.2525 1.0341 350.0908 0.9974 2.21 1.28 0.32 S5 双曲线 3.7677 0.0095 — 0.9990 2.34 1.29 0.64 MMF-Ⅱ 86.2061 1.0584 397.9812 0.9991 4.82 2.51 1.14 S6 双曲线 3.1247 0.0095 — 0.9978 1.42 0.92 0.24 MMF-Ⅱ 112.9076 0.9804 329.8660 0.9979 0.57 0.46 0.10 S7 双曲线 4.4275 0.0108 — 0.9944 2.15 −0.75 0.22 MMF-Ⅱ 71.2408 1.0794 416.6811 0.9946 1.30 0.64 0.13 S8 双曲线 9.8039 0.1899 — 0.9419 31.96 2.24 3.26 MMF-Ⅱ −1.0396 0.1205 −2.3030 0.9814 0.55 −0.05 0.11 S9 双曲线 7.9448 0.0288 — 0.9816 8.11 1.79 0.54 MMF-Ⅱ 35.3201 0.9936 274.5082 0.9999 7.88 1.74 0.53 S10 双曲线 5.5294 0.0167 — 0.9908 4.16 1.37 0.40 MMF-Ⅱ 166.3711 0.8423 540.3470 0.9917 3.30 −0.98 0.36 S11 双曲线 4.0073 0.0100 — 0.9981 3.51 1.75 0.69 MMF-Ⅱ 143.1599 0.9305 451.8395 0.9982 0.26 0.22 0.06 S12 双曲线 3.0885 0.0101 — 0.9981 5.40 3.11 1.01 MMF-Ⅱ 139.2267 0.9179 325.7170 0.9984 1.82 1.14 0.40 S13 双曲线 3.6537 0.0104 — 0.9989 2.59 1.37 0.68 MMF-Ⅱ 145.9022 0.9138 397.9244 0.9992 1.51 −0.60 0.72 S14 双曲线 4.4223 0.0123 — 0.9986 3.52 1.52 0.73 MMF-Ⅱ 74.2716 1.0255 358.6842 0.9986 4.61 1.96 0.94 S15 双曲线 3.8173 0.0093 — 0.9982 1.93 1.12 0.38 MMF-Ⅱ 77.3464 1.1049 426.3157 0.9986 6.28 3.26 1.20 S16 双曲线 3.3989 0.0084 — 0.9967 1.54 1.02 0.22 MMF-Ⅱ 160.0072 0.9428 447.0479 0.9968 1.24 −0.51 0.20 S17 双曲线 3.2720 0.0110 — 0.9968 5.66 3.08 0.78 MMF-Ⅱ 100.1378 0.9706 296.3921 0.9968 4.46 2.46 0.63 注:“—”表示无此参数。 由表3可知,除监测点S8因检验数据与建模数据变化不平稳,沉降曲线发展趋势发生明显变化,导致双曲线模型的外推预测误差较大外,其余监测点外推预测的MAPE值均小于10%,MFE值在−0.6~3.3,内拟合优度R2>0.98,多数监测点采用MMF-Ⅱ模型和双曲线模型的后验误差比均小于1,表明优选的MMF-Ⅱ模型、双曲线模型对不同监测点的沉降数据也具有较好的外推预测精度和内拟合优度,模型的适应性较强。
4.3 建模数据的时间跨度对预测结果的影响
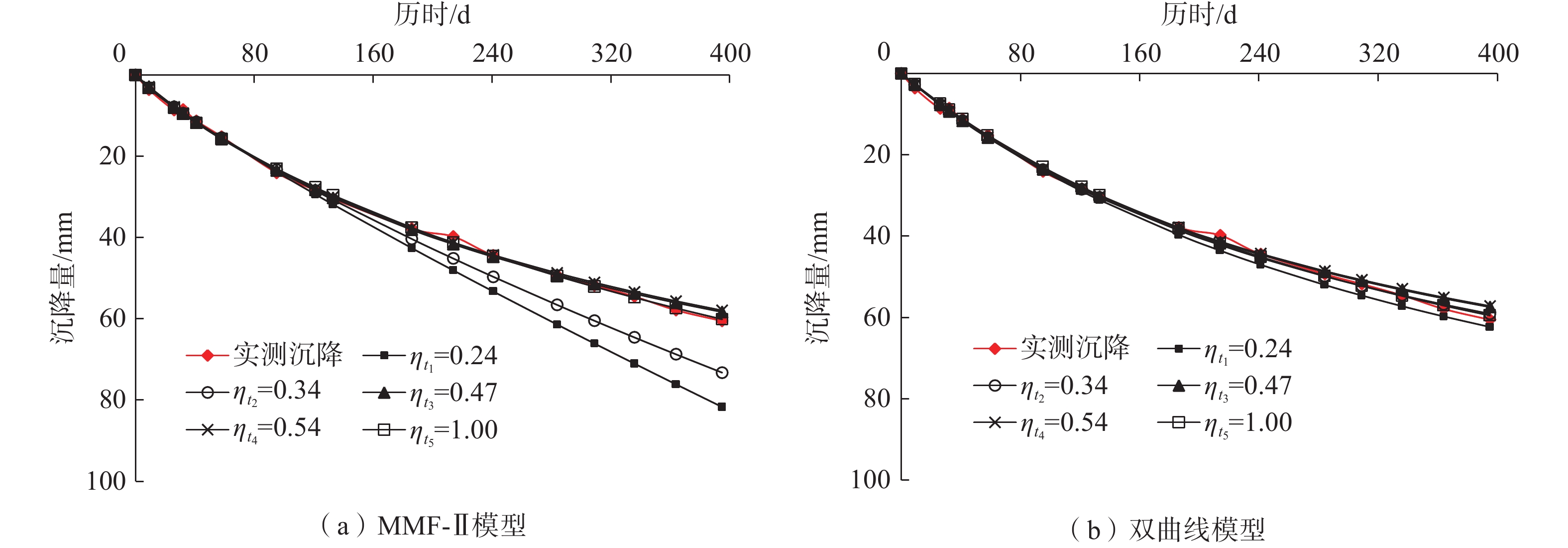
本实例中沉降观测时间为非等时间间隔,由于工后沉降曲线的变化与时间关系密切,仅以建模数据量的多少难以反映数据样本的选择不同对预测结果的影响。设建模数据时长与总数据时长之比为
$ \eta_{t_i} $ (i=1,2,···,n),本次分别取0.24、0.34、0.47、0.54、1.00,对应建模数据时长$t_i $ 为95 d、133 d、186 d、284 d、395 d。MMF-Ⅱ模型、双曲线模型的建模数据在不同时间跨度时预测结果如图5所示。由图5(a)可知,当$ \eta_{t_i} $ 为0.24、0.34时,MMF-Ⅱ模型的预测值较实测值偏大,当$ \eta_{t_i} $ 增大至0.47、0.54后,预测值较实测值总体偏小。当$ \eta_{t_i} $ 由0.24增大至0.34、0.47时,预测精度有明显提升,但是当$ \eta_{t_i} $ 由0.47增大至0.54时,预测精度变化不显著。由图5(b)可知,双曲线模型的$ \eta_{t_i} $ 为0.24时,预测值较实测值总体偏大,当$ \eta_{t_i} $ 增大至0.34、0.47、0.54后,预测值较实测值总体偏小,当$ \eta_{t_i} $ 由0.34增大至0.47和0.54时,预测精度提升不明显,表明该模型的适应性和稳定性好,能够较好地反映沉降曲线变化规律和发展趋势。当$ \eta_{t_i} $ =1.00时,此时为实测值的拟合曲线,此时可用于向外预测。总体而言,建模数据的时间跨度越大,模型从数据中提取的趋势信息越多,预测精度越高,但预测值趋向于偏小,数据的时间跨度增加到一定程度后,对预测效果的提升不再显著。5. 结论
(1)黄土高填方场地填方区的工后沉降曲线在土方填筑完成初期无陡增段,随时间增加沉降速率逐步降低,但观测期内尚未出现沉降趋于稳定的水平段;当遴选沉降预测模型时,建议将已有实测数据分成两部分,前一部分数据用于识别、估计模型及评价内拟合效果,后一部分数据用于检验模型外推预测的优劣程度,并将外推预测误差、内拟合误差和后验误差比最小化作为综合控制目标,可遴选出较理想的回归参数模型。
(2)当评价不同模型对相同沉降数据样本的预测效果时,建议外推预测效果评价指标采用MAPE、MAD、MSE结合MFE,内拟合效果评价指标采用SSE、RMSE、R2。当评价同一模型对不同沉降数据样本的适应性时,建议外推预测效果评价指标采用MAPE结合MFE,内拟合效果评价指标采用R2。
(3)MMF模型(Ⅱ型)和双曲线模型的外推预测误差小、内拟合优度高、后验误差比小,具有较高的预测精度、较好的稳定性和较强的适应性,能够较准确地反映黄土高填方场地工后沉降的变化规律和发展趋势,分别代表了“S”型曲线模型和“J”型曲线模型中预测效果较好的两种模型。
(4)MMF模型(Ⅱ型)和双曲线模型对本实例中“缓变型”沉降曲线的预测结果显示,实测数据的变化越平稳,模型的预测效果越好;建模数据的时间跨度越大,模型从数据中提取的信息越多,预测效果也越好,但时间跨度增大至一定程度后,对预测精度的提升不再显著。
-
表 1 沉降预测中常用的回归参数预测模型
Table 1 Summary of regression parameter prediction models for settlement prediction
类型 模型名称 数学表达式 沉降速率 备 注 第
Ⅰ
类
模
型Logistic ${\hat s_t} = a/(1 + b{{\text{e}}^{ - ct}})$ ${\hat s'_t} = abc{{\text{e}}^{ - ct}}/{(1 + b{{\text{e}}^{ - ct}})^2}$ 收敛模型 Gompertz ${\hat s_t} = a{{\text{e}}^{ - {{\text{e}}^{b - ct}}}}$ ${\hat s'_t} = ac{{\text{e}}^{ - {{\text{e}}^{b - ct}}}}{{\text{e}}^{b - ct}}$ 收敛模型 Usher ${\hat s_t} = a/{(1 + b{{\text{e}}^{ - ct}})^d}$ ${\hat s'_t} = abcd{{\text{e}}^{ - ct}}{(1 + b{{\text{e}}^{ - ct}})^{ - 1 - d}}$ 收敛模型 Weibull ${\hat s_t} = a(1 - b{{\text{e}}^{ - c{t^d}}})$ ${\hat s'_t} = abcd{{\text{e}}^{ - c{t^d}}}{t^{ - 1 + d}}$ 收敛模型 MMF-Ⅰ ${\hat s_t} = (ab + c{t^d})/(b + {t^d})$ ${\hat s'_t} = cd{t^{d - 1}}/(b + {t^d}) - d{t^{d - 1}} \cdot (ab + c{t^d})/{(b + {t^d})^2}$ 收敛模型 MMF-Ⅱ ${\hat s_t} = a{t^b}/(c + {t^b})$ ${\hat s'_t} = ab{t^{b - 1}}/(c + {t^b}) - ab{t^{2b - 1}}/{(c + {t^b})^2}$ 收敛模型 Richards ${\hat s_t} = a{(1 - b{{\text{e}}^{ - ct}})^{1/(1 - d)}}$ ${\hat s'_t} = abc{{\text{e}}^{ - ct}}{(1 - b{{\text{e}}^{ - ct}})^{d/(1 - d)}}/(1 - d)$ 收敛模型 Knothe-Ⅰ ${\hat s_t} = a{(1 - {{\text{e}}^{ - b{t^c}}})^d}$ ${\hat s'_t} = abcd{t^{c - 1}}{{\text{e}}^{ - b{t^c}}} \cdot {(1 - {{\text{e}}^{ - b{t^c}}})^{d - 1}}$ 收敛模型 Knothe-Ⅱ ${\hat s_t} = a{(1 - {{\text{e}}^{ - bt}})^c}$ ${\hat s'_t} = abc{{\text{e}}^{ - bt}}{(1 - {{\text{e}}^{ - bt}})^{c - 1}}$ 收敛模型 Bertalanffy ${\hat s_t} = {[{a^{1/3}} - {(a - b)^{1/3}} \cdot {{\text{e}}^{ - ct}}]^3}$ ${\hat s'_t} = 3{(a - b)^{1/3}}c{{\text{e}}^{ - ct}} \cdot {[{a^{1/3}} - {(a - b)^{1/3}} \cdot {{\text{e}}^{ - ct}}]^2}$ 收敛模型 邓英尔 ${\hat s_t} = a/(1 + b{{\text{e}}^{ - c{t^d}}})$ ${\hat s'_t} = abcd{{\text{e}}^{ - c{t^d}}}{t^{d - 1}}/{(1 + b{{\text{e}}^{ - c{t^d}}})^2}$ 收敛模型 第
Ⅱ
类
模
型Spillman ${\hat s_t} = a - (a - b){{\text{e}}^{ - ct}}$ ${\hat s'_t} = (a - b)c{{\text{e}}^{ - ct}}$ 收敛模型 指数曲线 ${\hat s_t} = a(1 - {{\text{e}}^{ - bt}})$ ${\hat s'_t} = ab{{\text{e}}^{ - bt}}$ 收敛模型 双曲线 ${\hat s_t} = t/(a + bt)$ ${\hat s'_t} = a/{(a + bt)^2}$ 收敛模型 幂函数 ${\hat s_t} = a{t^b}$ ${\hat s'_t} = ab{t^{b - 1}}$ 发散模型 平方根函数 ${\hat s_t} = a + b\sqrt t $ ${\hat s'_t} = b/2\sqrt t $ 发散模型 对数函数 ${\hat s_t} = a\ln t + b$ ${\hat s'_t} = a/t$ 发散模型 对数抛物线 ${\hat s_t} = a{(\lg t)^2} + b\lg t + c$ ${\hat s'_t} = \lg {\text{e}} \cdot (b + 2a\lg t) \cdot {t^{ - 1}}$ 发散模型 星野法 ${\hat s_t} = {s_0} + \dfrac{ {ab\sqrt {t - {t_0} } } }{ {\sqrt {1 + {b^2}\left( {t - {t_0} } \right)} } }$ ${\hat s'_t} = \dfrac{ {ab} }{ {2\sqrt {[1 + {b^2}(t - {t_0})](t - {t_0})} } } - \dfrac{ {a{b^3}\sqrt {t - {t_0} } } }{ {2{ {[1 + {b^2}(t - {t_0})]}^{3/2} } } }$ 收敛模型 表 2 各模型对典型监测点S6实测数据的内拟合及外推预测结果
Table 2 Internal-fitting and extrapolation prediction results of each model for the measured settlement data at a typical monitoring point S6
类型 模型名称 模型参数 内拟合效果 外推预测效果 后验误差
比Cia b c d MAPE* /% SSE RMSE R2 MAPE /% MAD MSE MFE 第
Ⅰ
类
模
型Logistic 39.7540 7.6080 0.0252 — 9.88 8.06 0.95 0.9928 21.66 11.77 179.32 11.77 2.19 Gompertz 43.7854 0.9395 0.0150 — 6.10 3.09 0.59 0.9973 16.39 8.99 111.11 8.99 2.69 Usher 64.0873 −0.9931 0.0049 −1.0149 5.16 2.72 0.52 0.9981 5.03 2.74 10.97 2.31 0.98 Weibull 3.3377 −52.2248 14.7577 −0.4232 3.58 2.04 0.45 0.9986 3.09 1.65 3.87 1.21 0.86 MMF-Ⅰ 2.4888 869.7498 68.8715 1.3199 3.26 1.71 0.44 0.9985 7.18 3.93 21.54 3.62 2.20 MMF-Ⅱ 113.9160 0.9777 329.4676 — 5.84 3.04 0.55 0.9979 2.05 1.05 1.77 0.41 0.35 Richards 51.8874 0.8687 0.0085 0.3724 3.18 1.66 0.43 0.9985 9.98 5.49 42.78 5.25 3.13 Knothe-Ⅰ 41.0949 0.0000 4.0687 0.2098 4.49 2.17 0.49 0.9981 18.75 10.31 147.80 10.31 4.18 Knothe-Ⅱ 68.6817 240.2071 0.9562 — 5.65 2.87 0.56 0.9975 3.79 2.05 6.41 1.58 0.67 Bertalanffy 46.8972 36.1948 0.0116 — 4.45 2.03 0.47 0.9982 13.42 7.39 76.86 7.32 3.02 邓英尔 3.2623 −0.9558 28.7664 −1.2368 3.24 1.81 0.42 0.9987 6.32 3.45 16.62 3.11 1.95 第
Ⅱ
类
模
型Spillman 68.5727 0.7074 0.0043 — 4.50 2.47 0.52 0.9978 3.59 1.93 5.67 1.38 0.80 指数曲线 62.6226 0.0050 — — 5.95 3.01 0.58 0.9973 5.71 3.12 13.95 2.74 0.96 双曲线 3.1221 0.0095 — — 6.00 3.06 0.55 0.9979 2.75 1.46 3.16 0.93 0.46 幂函数 0.6425 0.7852 — — 4.34 5.38 0.73 0.9963 11.67 6.15 42.57 -6.15 2.69 平方根函数 −8.9505 3.3748 — — 13.18 14.00 1.25 0.9876 2.90 1.54 2.78 1.36 0.22 对数函数 11.6931 −28.2990 — — 26.75 113.31 3.55 0.8993 24.20 12.77 182.58 12.77 0.90 对数抛物线 21.4982 −43.5385 25.8604 — 4.12 2.83 0.56 0.9975 2.75 1.46 2.83 1.07 0.67 星野法 1367.0000 0.0018 — — 32.50 114.39 3.38 0.9205 16.81 8.80 84.05 8.80 0.52 注:“—”表示无此参数。 表 3 优选模型对不同监测点沉降数据的内拟合和外推预测结果
Table 3 Internal-fitting and extrapolation prediction of settlement data for different monitoring points using the optimal model
监测点 模型名称 模型参数 内拟合效果
R2外推预测效果 后验误差比
Cia b c MAPE /% MFE S2 双曲线 15.8265 0.0747 — 0.9805 8.33 −0.60 0.58 MMF-Ⅱ 7.4942 1.5515 829.1400 0.9880 7.42 0.56 0.55 S3 双曲线 4.9610 0.0145 — 0.9969 3.28 1.31 0.73 MMF-Ⅱ 64.7724 1.0199 344.1345 0.9969 4.11 1.60 0.88 S4 双曲线 3.4475 0.0099 — 0.9973 0.78 0.56 0.12 MMF-Ⅱ 90.2525 1.0341 350.0908 0.9974 2.21 1.28 0.32 S5 双曲线 3.7677 0.0095 — 0.9990 2.34 1.29 0.64 MMF-Ⅱ 86.2061 1.0584 397.9812 0.9991 4.82 2.51 1.14 S6 双曲线 3.1247 0.0095 — 0.9978 1.42 0.92 0.24 MMF-Ⅱ 112.9076 0.9804 329.8660 0.9979 0.57 0.46 0.10 S7 双曲线 4.4275 0.0108 — 0.9944 2.15 −0.75 0.22 MMF-Ⅱ 71.2408 1.0794 416.6811 0.9946 1.30 0.64 0.13 S8 双曲线 9.8039 0.1899 — 0.9419 31.96 2.24 3.26 MMF-Ⅱ −1.0396 0.1205 −2.3030 0.9814 0.55 −0.05 0.11 S9 双曲线 7.9448 0.0288 — 0.9816 8.11 1.79 0.54 MMF-Ⅱ 35.3201 0.9936 274.5082 0.9999 7.88 1.74 0.53 S10 双曲线 5.5294 0.0167 — 0.9908 4.16 1.37 0.40 MMF-Ⅱ 166.3711 0.8423 540.3470 0.9917 3.30 −0.98 0.36 S11 双曲线 4.0073 0.0100 — 0.9981 3.51 1.75 0.69 MMF-Ⅱ 143.1599 0.9305 451.8395 0.9982 0.26 0.22 0.06 S12 双曲线 3.0885 0.0101 — 0.9981 5.40 3.11 1.01 MMF-Ⅱ 139.2267 0.9179 325.7170 0.9984 1.82 1.14 0.40 S13 双曲线 3.6537 0.0104 — 0.9989 2.59 1.37 0.68 MMF-Ⅱ 145.9022 0.9138 397.9244 0.9992 1.51 −0.60 0.72 S14 双曲线 4.4223 0.0123 — 0.9986 3.52 1.52 0.73 MMF-Ⅱ 74.2716 1.0255 358.6842 0.9986 4.61 1.96 0.94 S15 双曲线 3.8173 0.0093 — 0.9982 1.93 1.12 0.38 MMF-Ⅱ 77.3464 1.1049 426.3157 0.9986 6.28 3.26 1.20 S16 双曲线 3.3989 0.0084 — 0.9967 1.54 1.02 0.22 MMF-Ⅱ 160.0072 0.9428 447.0479 0.9968 1.24 −0.51 0.20 S17 双曲线 3.2720 0.0110 — 0.9968 5.66 3.08 0.78 MMF-Ⅱ 100.1378 0.9706 296.3921 0.9968 4.46 2.46 0.63 注:“—”表示无此参数。 -
[1] 高建中, 郑建国, 魏弋锋, 等. 延安新区黄土丘陵沟壑区域工程造地实践[M]. 北京: 中国建筑工业出版社, 2019 GAO Jianzhong, ZHENG Jianguo, WEI Yifeng, et al. Engineering practice of land reclamation in loess hilly gully areas in Yan’an an new district[M]. Beijing: China Architecture & Building Press, 2019. (in Chinese with English abstract)
[2] 朱才辉,李宁,刘明振,等. 吕梁机场黄土高填方地基工后沉降时空规律分析[J]. 岩土工程学报,2013,35(2):293 − 301. [ZHU Caihui,LI Ning,LIU Mingzhen,et al. Spatiotemporal laws of post-construction settlement of loess-filled foundation of LYUliang Airport[J]. Chinese Journal of Geotechnical Engineering,2013,35(2):293 − 301. (in Chinese with English abstract) ZHU Caihui, LI Ning, LIU Mingzhen, et al. Spatiotemporal laws of post-construction settlement of loess-filled foundation of Lüliang Airport[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 293-301. (in Chinese with English abstract)
[3] 姚仰平,黄建,张奎,等. 机场高填方蠕变沉降的数值反演预测[J]. 岩土力学,2020,41(10):3395 − 3404. [YAO Yangping,HUANG Jian,ZHANG Kui,et al. Numerical back-analysis of creep settlement of airport high fill[J]. Rock and Soil Mechanics,2020,41(10):3395 − 3404. (in Chinese with English abstract) DOI: 10.16285/j.rsm.2020.0402 YAO Yangping, HUANG Jian, ZHANG Kui, et al. Numerical back-analysis of creep settlement of airport high fill[J]. Rock and Soil Mechanics, 2020, 41(10): 3395-3404. (in Chinese with English abstract) DOI: 10.16285/j.rsm.2020.0402
[4] 宰金珉,梅国雄. 全过程的沉降量预测方法研究[J]. 岩土力学,2000,21(4):322 − 325. [ZAI Jinmin,MEI Guoxiong. Forecast method of settlement during the complete process of construction and operation[J]. Rock and Soil Mechanics,2000,21(4):322 − 325. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-7598.2000.04.003 ZAI Jinmin, MEI Guoxiong. Forecast method of settlement during the complete process of construction and operation[J]. Rock and Soil Mechanics, 2000, 21(4): 322-325. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-7598.2000.04.003
[5] 刘射洪, 袁聚云, 赵昕. 地基沉降预测模型研究综述[J]. 工业建筑, 2014, 44(增刊1): 738 − 741 LIU Shehong, YUAN Juyun, ZHAO Xin. Review of settlement prediction models of foundation[J]. Industrial Construction, 2014, 44(Sup 1): 738 − 741. (in Chinese with English abstract)
[6] 周艳萍. 基于灰色Verhulst模型的山西太原地面沉降趋势分析[J]. 中国地质灾害与防治学报,2018,29(2):94 − 99. [ZHOU Yanping. Land subsidence trend of Taiyuan City,Shanxi based on Grey Verhust Model[J]. The Chinese Journal of Geological Hazard and Control,2018,29(2):94 − 99. (in Chinese with English abstract) DOI: 10.16031/j.cnki.issn.1003-8035.2018.02.15 ZHOU Yanping. Land subsidence trend of Taiyuan City, Shanxi based on Grey Verhust Model[J]. The Chinese Journal of Geological Hazard and Control, 2018, 29(2): 94-99. (in Chinese with English abstract) DOI: 10.16031/j.cnki.issn.1003-8035.2018.02.15
[7] 范珊珊,郭海朋,朱菊艳,等. 线性回归模型在北京平原地面沉降预测中的应用[J]. 中国地质灾害与防治学报,2013,24(1):70 − 74. [FAN Shanshan,GUO Haipeng,ZHU Juyan,et al. Application of linear regression model for land subsidence prediction in Beijing plain[J]. The Chinese Journal of Geological Hazard and Control,2013,24(1):70 − 74. (in Chinese with English abstract) DOI: 10.16031/j.cnki.issn.1003-8035.2013.01.016 FAN Shanshan, GUO Haipeng, ZHU Juyan, et al. Application of linear regression model for land subsidence prediction in Beijing plain[J]. The Chinese Journal of Geological Hazard and Control, 2013, 24(1): 70-74. (in Chinese with English abstract) DOI: 10.16031/j.cnki.issn.1003-8035.2013.01.016
[8] 韩相超,吕远强. 内蒙古黄旗海湿地软土路基的沉降规律分析[J]. 中国地质灾害与防治学报,2013,24(1):75 − 78. [HAN Xiangchao,LYU Yuanqiang. Settlement analysis of soft subgrade in Huangqihai wetlands,Inner Mongolia[J]. The Chinese Journal of Geological Hazard and Control,2013,24(1):75 − 78. (in Chinese with English abstract) DOI: 10.16031/j.cnki.issn.1003-8035.2013.01.005 HAN Xiangchao, LV Yuanqiang. Settlement analysis of soft subgrade in Huangqihai wetlands, Inner Mongolia[J]. The Chinese Journal of Geological Hazard and Control, 2013, 24(1): 75-78. (in Chinese with English abstract) DOI: 10.16031/j.cnki.issn.1003-8035.2013.01.005
[9] 葛苗苗,李宁,郑建国,等. 基于一维固结试验的压实黄土蠕变模型[J]. 岩土力学,2015,36(11):3164 − 3170. [GE Miaomiao,LI Ning,ZHENG Jianguo,et al. A creep model for compacted loess based on 1D oedometer test[J]. Rock and Soil Mechanics,2015,36(11):3164 − 3170. (in Chinese with English abstract) DOI: 10.16285/j.rsm.2015.11.017 GE Miaomiao, LI Ning, ZHENG Jianguo, et al. A creep model for compacted loess based on 1D oedometer test[J]. Rock and Soil Mechanics, 2015, 36(11): 3164-3170. (in Chinese with English abstract) DOI: 10.16285/j.rsm.2015.11.017
[10] 宰金珉,梅国雄. 泊松曲线的特征及其在沉降预测中的应用[J]. 重庆建筑大学学报,2001,23(1):30 − 35. [ZAI Jinmin,MEI Guoxiong. Feature of poisson curve and its application to displacement forecast[J]. Journal of Chongqing Jianzhu University,2001,23(1):30 − 35. (in Chinese with English abstract) ZAI Jinmin, MEI Guoxiong. Feature of Poisson curve and its application to displacement forecast[J]. Journal of Chongqing Jianzhu University, 2001, 23(1): 30-35. (in Chinese with English abstract)
[11] 曹文贵, 印鹏, 贺敏, 等. 考虑实测数据新旧程度的恭候澄江单项模型预测方法[J]. 水文地质工程地质, 2015, 42(6): 65 − 70 CAO Wengui, YIN Peng, HE Min, et al. A prediction method for post-construction settlement ofa single model with the consideration of the new or old degree of the measured data[J]. Hydrogeology & Engineering Geology, 2015, 42(6): 65 − 70. (in Chinese with English abstract)
[12] VAGHI C,RODALLEC A,FANCIULLINO R,et al. Population modeling of tumor growth curves and the reduced Gompertz model improve prediction of the age of experimental tumors[J]. PLoS Computational Biology,2020,16(2):e1007178. DOI: 10.1371/journal.pcbi.1007178
[13] 余闯,刘松玉. 路堤沉降预测的Gompertz模型应用研究[J]. 岩土力学,2005,26(1):82 − 86. [YU Chuang,LIU Songyu. A Study on prediction of embankment settlement with the gompertz model[J]. Rock and Soil Mechanics,2005,26(1):82 − 86. (in Chinese with English abstract) YU Chuang, LIU Songyu. A Study on prediction of embankment settlement with the gompertz model[J]. Rock and Soil Mechanics, 2005, 26(1): 82-86. (in Chinese with English abstract)
[14] 胡顺强,崔东文. 基于AEO-Schumacher-Usher模型的径流及地下水位预测[J]. 中国农村水利水电,2020(11):28 − 34. [HU Shunqiang,CUI Dongwen. Runoff and groundwater level prediction based on AEO-schumacher-usher model[J]. China Rural Water and Hydropower,2020(11):28 − 34. (in Chinese with English abstract) DOI: 10.3969/j.issn.1007-2284.2020.11.006 HU Shunqiang, CUI Dongwen. Runoff and groundwater level prediction based on AEO-schumacher-usher model[J]. China Rural Water and Hydropower, 2020(11): 28-34. (in Chinese with English abstract) DOI: 10.3969/j.issn.1007-2284.2020.11.006
[15] DE OLIVEIRA FERREIRA D J,DE MATTOS FIUZA M P,CARDOSO M,et al. Use of the Weibull model on sizing thickeners-Part I:Sedimentation curve representation[J]. The Canadian Journal of Chemical Engineering,2021,99(3):708 − 724. DOI: 10.1002/cjce.23904
[16] 刘国辉. Weibull模型在地基沉降预测中的应用[J]. 贵州大学学报(自然科学版),2011,28(2):111 − 114. [LIU Guohui. The application of weibull model to settlement prediction of foundation[J]. Journal of Guizhou University (Natural Sciences),2011,28(2):111 − 114. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-5269.2011.02.029 LIU Guohui. The application of weibull model to settlement prediction of foundation[J]. Journal of Guizhou University (Natural Sciences), 2011, 28(2): 111-114. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-5269.2011.02.029
[17] 王军保,刘新荣,李鹏,等. MMF模型在采空区地表沉降预测中的应用[J]. 煤炭学报,2012,37(3):411 − 415. [WANG Junbao,LIU Xinrong,LI Peng,et al. Study on prediction of surface subsidence in mined-out region with the MMF model[J]. Journal of China Coal Society,2012,37(3):411 − 415. (in Chinese with English abstract) DOI: 10.13225/j.cnki.jccs.2012.03.024 WANG Junbao, LIU Xinrong, LI Peng, et al. Study on prediction of surface subsidence in mined-out region with the MMF model[J]. Journal of China Coal Society, 2012, 37(3): 411-415. (in Chinese with English abstract) DOI: 10.13225/j.cnki.jccs.2012.03.024
[18] ZREIQ R,KAMEL S,BOUBAKER S,et al. Generalized Richards model for predicting COVID-19 dynamics in Saudi Arabia based on particle swarm optimization Algorithm[J]. AIMS Public Health,2020,7(4):828 − 843. DOI: 10.3934/publichealth.2020064
[19] HUANG Changfu,LI Qun,WU Shunchuan,et al. Application of the richards model for settlement prediction based on a bidirectional difference-weighted least-squares method[J]. Arabian Journal for Science and Engineering,2018,43(10):5057 − 5065. DOI: 10.1007/s13369-017-2909-0
[20] HU Qingfeng,CUI Ximin,WANG Guo,et al. Key technology of predicting dynamic surface subsidence based on knothe time function[J]. Journal of Software,2011,6(7):1273 − 1280.
[21] CHEN Lei,ZHANG Liguo,TANG Yixian,et al. Analysis of mining-induced subsidence prediction by exponent knothe model combined with insar and leveling[J]. ISPRS Annals of the Photogrammetry,Remote Sensing and Spatial Information Sciences,2018,IV-3:53 − 59.
[22] 高超,徐乃忠,孙万明,等. 基于Bertalanffy时间函数的地表动态沉陷预测模型[J]. 煤炭学报,2020,45(8):2740 − 2748. [GAO Chao,XU Naizhong,SUN Wanming,et al. Dynamic surface subsidence prediction model based on Bertalanffy time function[J]. Journal of China Coal Society,2020,45(8):2740 − 2748. (in Chinese with English abstract) GAO Chao, XU Naizhong, SUN Wanming, et al. Dynamic surface subsidence prediction model based on Bertalanffy time function[J]. Journal of China Coal Society, 2020, 45(8): 2740-2748. (in Chinese with English abstract)
[23] LEE L,ATKINSON D,HIRST A G,et al. A new framework for growth curve fitting based on the von Bertalanffy Growth Function[J]. Scientific Reports,2020,10(1):1 − 12. DOI: 10.1038/s41598-019-56847-4
[24] 邓英尔,谢和平. 全过程沉降预测的新模型与方法[J]. 岩土力学,2005,26(1):1 − 4. [DENG Yinger,XIE Heping. New model and method of forecasting settlement during complete process of construction and operation[J]. Rock and Soil Mechanics,2005,26(1):1 − 4. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-7598.2005.01.001 DENG Yinger, XIE Heping. New model and method of forecasting settlement during complete process of construction and operation[J]. Rock and Soil Mechanics, 2005, 26(1): 1-4. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-7598.2005.01.001
[25] 王志亮,吴克海,李永池,等. 一个预测路堤沉降的新经验公式模型[J]. 岩石力学与工程学报,2005,24(12):2013 − 2017. [WANG Zhiliang,WU Kehai,LI Yongchi,et al. A new empirical formula model for settlement prediction of embankments[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(12):2013 − 2017. (in Chinese with English abstract) DOI: 10.3321/j.issn:1000-6915.2005.12.003 WANG Zhiliang, WU Kehai, LI Yongchi, et al. A new empirical formula model for settlement prediction of embankments[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(12): 2013-2017. (in Chinese with English abstract) DOI: 10.3321/j.issn:1000-6915.2005.12.003
[26] REDDY B R,OJHA A. Performance of maintainabilityiindex prediction models:A feature selection based study[J]. Evolving Systems,2019,10(2):179 − 204. DOI: 10.1007/s12530-017-9201-0
[27] 方薇,陈向阳.考虑次固结的软基分级加载全过程沉降模型[J].中国地质灾害与防治学报, 2015, 26(2): 110-115 FANG Wei, CHEN Xiangyang.Foundation settlement model considering secondary consolidation during multi-stage loading[J]. The Chinese Journal of Geological Hazard andControl, 2015, 26(2): 110-115.(in Chinese with English abstract)
[28] 韩相超, 吕远强.内蒙古黄旗海湿地软土路基的沉降规律分析[J].中国地质灾害与防治学报, 2013, 24(1): 75-78. HAN Xiangchao, LYU Yuanqiang. Settlement analysis of soft subgrade in Huangqihai wetlands, Inner Mongolia[J]. The Chinese Journal of Geological Hazard and Control, 2013, 24(1): 75-78.(in Chinese with English abstract)
[29] LI Shouju,YU Shen,SHANGGUAN Zichang,et al. Estimating model parameters of rockfill materials based on genetic algorithm and strain measurements[J]. Geomechanics and Engineering,2016,10(1):37 − 48. DOI: 10.12989/gae.2016.10.1.037
[30] 甘友文,王志亮, 郑华.地基沉降预测中的双曲线模型修正[J].水文地质工程地质, 2004, 31(1): 98-100. GAN Youwen, WANG Zhiliang, ZHENG Hua. Modification of hyperbolic model in foundation settlement prediction[J]. Hydrogeology & Engineering Geology, 2004, 31(1): 98-100.(in Chinese)
[31] 刘宏,李攀峰,张倬元. 九寨黄龙机场高填方地基工后沉降预测[J]. 岩土工程学报,2005,27(1):90 − 93. [LIU Hong,LI Panfeng,ZHANG Zhuoyuan. Prediction of the post-construction settlement of the high embankment of Jiuzhai-Huanglong Airport[J]. Chinese Journal of Geotechnical Engineering,2005,27(1):90 − 93. (in Chinese with English abstract) DOI: 10.3321/j.issn:1000-4548.2005.01.015 LIU Hong, LI Panfeng, ZHANG Zhuoyuan. Prediction of the post-construction settlement of the high embankment of Jiuzhai-Huanglong Airport[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 90-93. (in Chinese with English abstract) DOI: 10.3321/j.issn:1000-4548.2005.01.015
[32] 王海英,常肖,阮祺,等. 建筑垃圾填埋路基沉降预测的三点-星野法[J]. 铁道科学与工程学报,2017,14(3):473 − 479. [WANG Haiying,CHANG Xiao,RUAN Qi,et al. Subsidence prediction of subgrade filled by construction waste based on three point-hoshino algorithm[J]. Journal of Railway Science and Engineering,2017,14(3):473 − 479. (in Chinese with English abstract) DOI: 10.3969/j.issn.1672-7029.2017.03.006 WANG Haiying, CHANG Xiao, RUAN Qi, et al. Subsidence prediction of subgrade filled by construction waste based on three point-hoshino algorithm[J]. Journal of Railway Science and Engineering, 2017, 14(3): 473-479. (in Chinese with English abstract) DOI: 10.3969/j.issn.1672-7029.2017.03.006
[33] 中华人民共和国住房和城乡建设部. 建筑变形测量规范: JGJ 8—2016[S]. 北京: 中国建筑工业出版社, 2016 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for deformation measurement of building and structure: JGJ 8—2016[S]. Beijing: China Architecture & Building Press, 2016. (in Chinese)
[34] LEWIS C D. Industrial and business forecasting methods: A practical guide to exponential smoothing and curve fitting[M]. London: Butterworth Scientific, 1982.




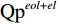
 下载:
下载:
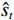
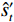
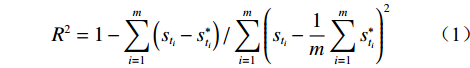
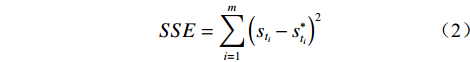
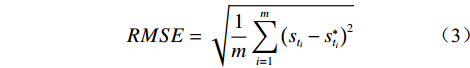
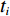
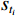
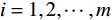
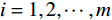
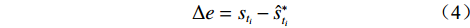
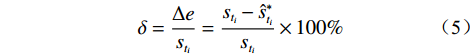
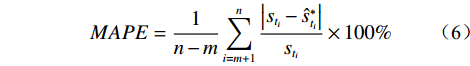
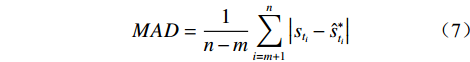
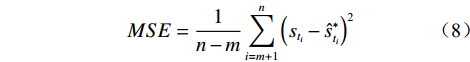
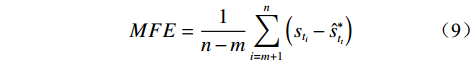
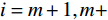
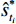
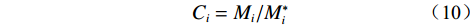
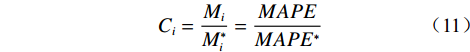
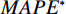
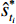
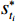
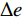
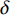
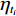
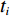
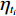
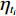
 邮件订阅
邮件订阅 RSS
RSS