0.   引言

南水北调中线工程渠首段位于河南省南阳市，渠段内土体多为膨胀土。膨胀土是在自然地质过程中形成的一种具有显著胀缩性且裂隙发育的特殊土体，对于环境变化、特别是湿热变化非常敏感，且膨胀土的存在会改变周围土体的工程地质特征。因此渠首段渠坡的渗透特性与一般的黏性土边坡不同，这会导致排水措施的效果与期望排水效果有差异^[1]。且相比于一般土体的渗透特性，膨胀土的裂隙发育程度会影响到其渗透性变化过程^[2]。因此，探究膨胀土裂隙发育特征与其渗透性之间的关系，从而确定渠坡段排水措施的实际排水效果是十分必要的。

国内外学者们对于土体渗流特性的研究已经十分深入。在最初进行的渗流场研究中，学者们的研究方向主要集中在饱和渗流场，如Henry Darcy发现的层流状态下饱和土体的渗透定律―达西定律。但对于非饱和区域的土体，达西定律的应用存在局限性。后续学者在达西研究的基础上进行了深度的研究，取得了一些成果。对于那些超出达西定律的流动，Forchheimer提出了非达西渗流运动方程，蒙学礼等^[3]在此基础上计算出了非线性系数及渗透率，雷怡等^[4]将剖面二维潜水运动方程作为控制方程，结合排水前坡体渗流场作为初始条件，理论推导并创新地得到了潜水面边界条件。Richard^[5]提出了Richard渗流控制方程，其将达西的线性渗流理论应用到非饱和渗流理论研究中，师文豪等^[6]基于等效连续介质模型和Louis经验公式建立的各向异性岩体渗流应力耦合模型，对顺倾向层状边坡的各向异性渗流规律进行了模拟和总结。Jacob^[7]基于质量守恒定律提出了渗流连续性方程，并在工程渗流计算中得到广泛应用。饱和情况下的渗流微分方程的解析解可直接得到；而对非饱和渗流，其渗流微分方程是非线性的，直接求解非常困难。随着计算机技术的发展，学者们开始应用有限元方法来进行渗流场的求解。Zienkiewicz^[8]等最早将有限元法引用到流体力学领域，Finn^[9]等将有限单元法运用到稳定渗流领域。Neuman^[10]等将有限元发展到非稳定渗流计算中。Fredlund^[11]在达西定律的基础上推导了饱和-非饱和渗流微分控制方程，并将其应用到几个瞬态渗流问题的数值分析中。

对于非饱和膨胀土来讲，基质吸力是影响其渗透性的重要因素，Thakur等^[12]与Al-Mahbashi等^[13]都对土的基质吸力进行了相关研究，证明了基质吸力和含水率的关系，深入研究非饱和膨胀土渗透特征，并发现了膨胀土吸力测定技术固有的滞后现象，且这种滞后性与土的特性无关。这将部分学者的研究视野带向了土—水特征曲线，Sillers^[14]和Sillers 等^[15]研究了用于表示土—水特征曲线的相关数学模型，并采用非线性最小二乘法确定了一些经验方程较好的拟合参数；李萍等^[16]测量出土—水特征曲线并计算了渗透系数与含水率的关系，张琦等^[17]探究冻融循环条件下初始含水率对膨胀土偏应力应变关系和剪切特性的影响，发现初始含水率是 影 响 非饱和膨胀土力学性质的主要原因。这些研究成果都为非饱和渗透提供了理论依据，为非饱和渗透的预测打下基础，如李志清等^[18]通过6种测量SWCC的方法预测了渗透系数的数学模型；马洪波等^[19]基于预测渗透系数的数学模型计算出了非饱和填料的渗透系数。这些预测非饱和渗透的数学模型对裂隙发育的膨胀土边坡渗透性提供了重要的参考，袁俊平等^[20]建立了考虑裂隙的非饱和膨胀土边坡入渗的数学模型，利用有限元方法对裂隙特征与渗透特征进行了分析；陈铁林^[21]基于非饱和土广义固结理论，对膨胀土边坡进行了有限元计算分析，与膨胀土边坡无裂隙的情况进行了对比，吕建航等^[22]通过实验发现土工格栅可约束膨胀土冻融裂缝,使裂缝发育更为均匀一致,同时减小边坡位移。王玮等^[23]在此基础上提出了估算裂隙与渗透系数关系的PNC模型，为探究膨胀土裂隙性与渗透性的关系建立了理论基础。

上述的学者都对膨胀土的非饱和渗透性，以及膨胀土裂隙对于其渗透性的影响方面有了一定的探索，本文在此基础上，设计了裂隙型膨胀土渗透过程室内试验模型，针对膨胀土渗透性随渗透时长的变化进行研究。通过模拟裂隙型膨胀土的渗流过程，进行了膨胀土从不同初始状态到达到渗流稳定状态的渗流试验，探究裂隙型膨胀土的渗透系数变化与初始含水率、初始裂隙率的关系。分析由于初始含水率、初始裂隙率的变化所导致的土体渗透性发生波动的原因，并依据上述结果分析渠坡排水效果。

1.   裂隙型膨胀土渗透过程模型

1.1   试样基本参数

试样取自河南南阳市淅川县南水北调工程渠坡附近，在获取土样后依据《土工试验方法标准》（GB/T 50123—1999）对样品进行室内土工试验，获取试样参数。

将样品进行编号后，对1—5号土样进行了含水率测试、重度测试以及抗剪强度测试。获取的基本参数指标见表1。

表  1  试样基本参数指标

Table  1.  Fundamental parameters of test samples

编号	含水率/%	重度/（kN·m−3）	黏聚力/kPa	内摩擦角/（°）
1	12.4	19.1	14.0	11.0
2	10.1	22.1	20.0	14.0
3	25.4	19.7	24.0	16.0
4	29.1	19.9	61.3	22.8
5	28.2	20.3	72.5	25.0

下载: 导出CSV 

| 显示表格

1.2   模型建立及试验原理

由于土体经历自然蒸发所产生的裂隙具有随机性，是研究裂隙率和膨胀土体渗透性的不可控因素。因此，建立一个能够定量控制土体裂隙率的试验模型尤为重要。当相应的模型建立之后，通过控制其初始条件，对土体进行渗流试验，获取关于渗透系数的变化曲线，即可研究膨胀土裂隙率与渗透系数的关系。

渗透试验采用常水头方法来计算裂隙型膨胀土的渗透系数，渗透系数($ k $)的计算公式：

式中：Q——$ t $时间段内渗透经过试样的水质量/g；

ρ_w——水的密度/（g·cm⁻³）；

L——试样的有效长度/cm；

A——试件的横切面面积/cm²；

(h₁－h₂)——水头差/cm。

试验开始时，从进水口注水至模型两侧形成所需要的水头差，并在出水口处设置量筒，等到有水渗出时记录时间和渗出水量，通过计算得到膨胀土的渗透系数。

1.3   试验方法

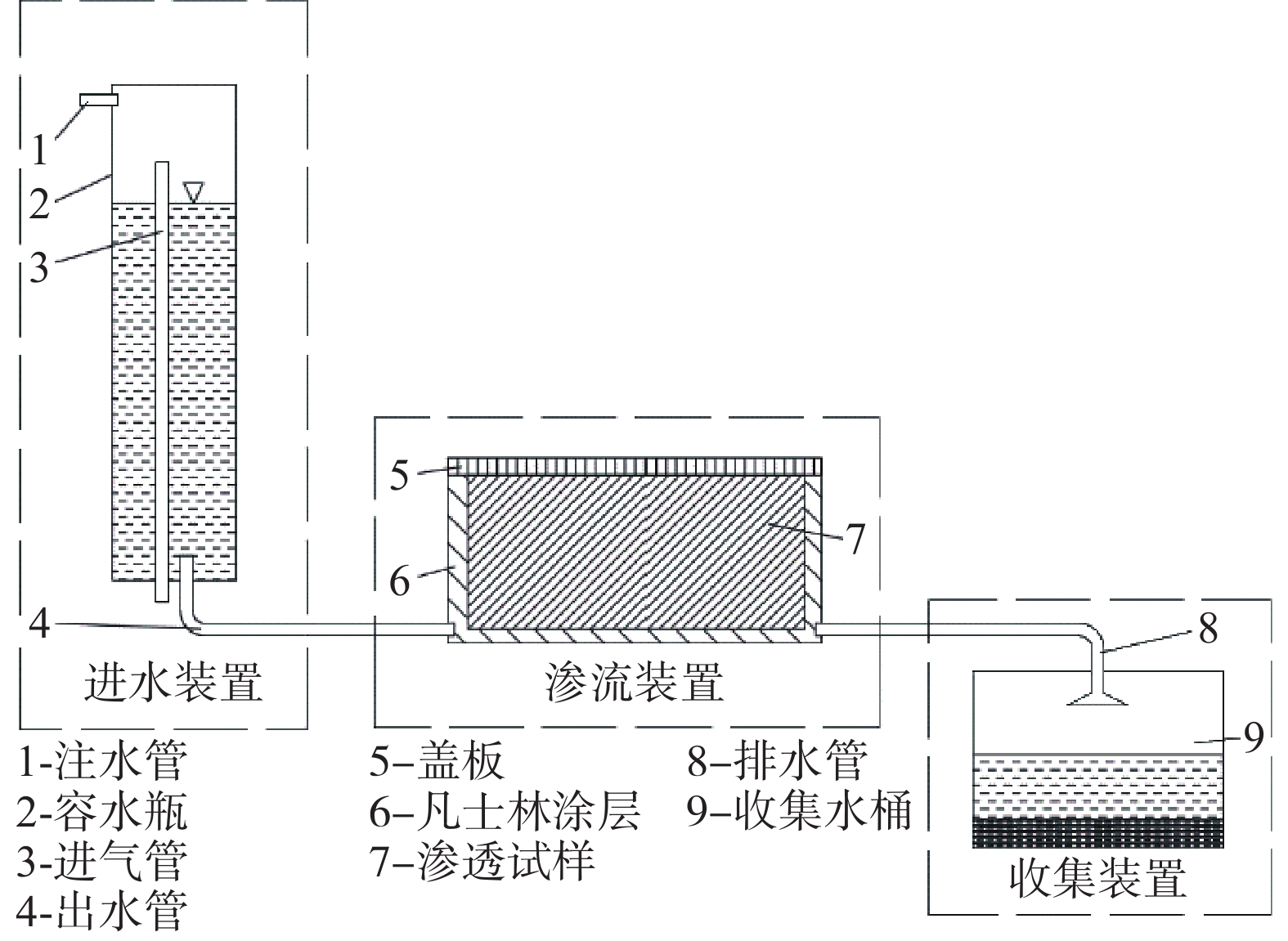
图1为测试裂隙型膨胀土渗透系数的试验装置，由马利奥特瓶、渗透装置和过滤装置组成。渗透装置共分三个实验仓，两端为砾石组成的过滤仓，中间为渗透仓。

图  1  装置示意图

Figure  1.  Schematic diagram of the self-made permeability apparatus

下载: 全尺寸图片 幻灯片

将土样风干并用粉碎机粉碎，过2 mm筛，其风干含水率为5%。将土样置于容器中加入适量的水，进行充分搅拌，由于膨胀土吸水能力强，此处搅拌要使土中迅速吸水形成的团块散开。

控制土样初始含水率为25%。为使土样中的水分分布均匀，将土样装入塑料袋密封72 h。然后称取适量的土样制成土条，按要求置于模型之中。

在土样自然干燥过程中分别设定了5个含水率控制标准：25%、20%、15%、10%、5%。将部分压制好的试样密封保存并制成土条，其初始含水率为25%，将其他剩余试样置于蒸发皿中，在自然条件下进行干燥（温度：20℃左右），每隔6 h对样品称重，根据重量变化计算膨胀土样品的含水率。当试样含水率达到上述控制标准时，选取试样并密封保存96 h，让水分进一步分布均匀。在测试过程中，确保每个控制标准至少使用5个平行样进行试验。

根据现场的裂隙条数、宽度、长度数据概化^[24]，设置不同初始裂隙率从4%、6.5%、9%、11.5%、14%，共计5个等级。

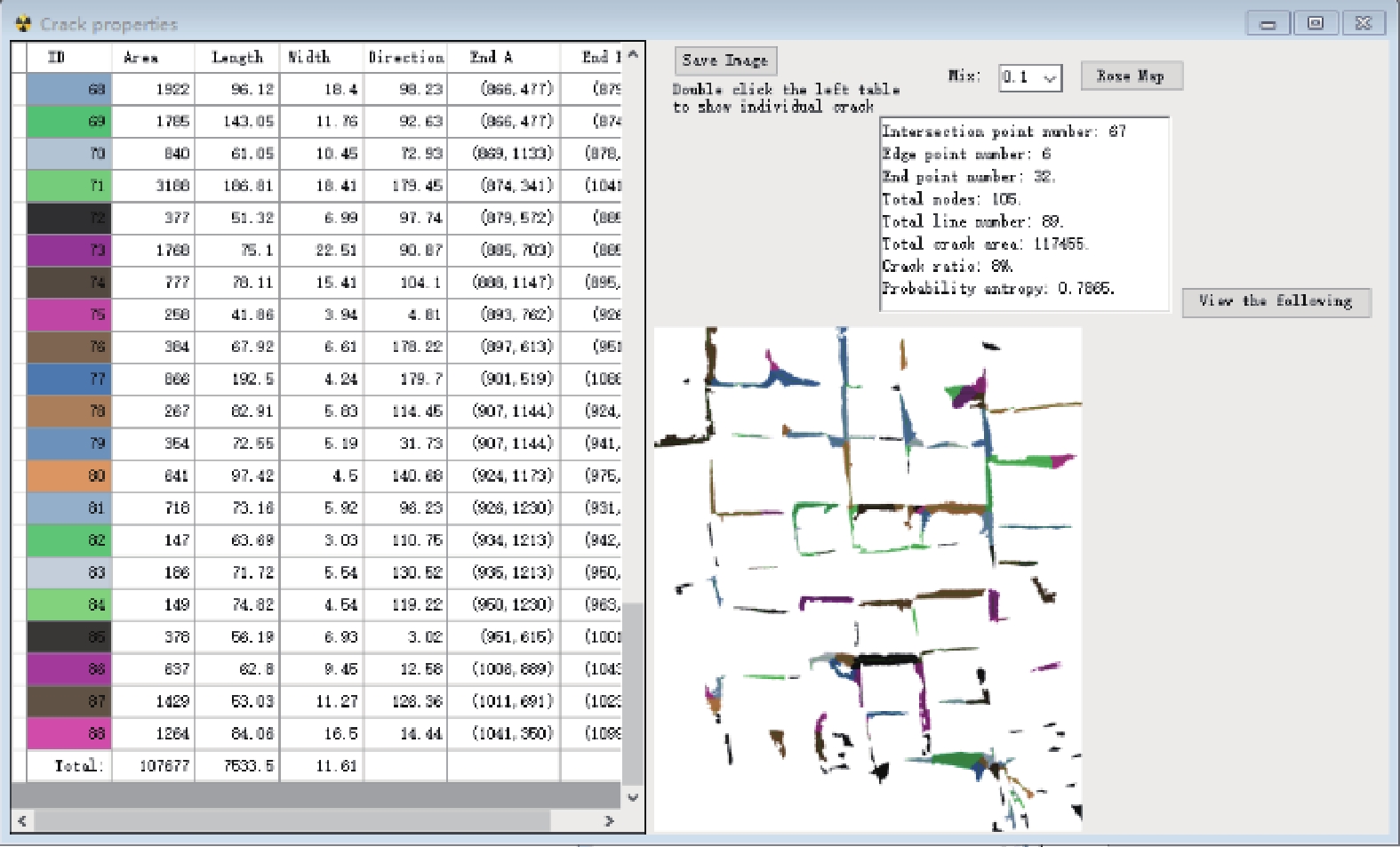
将上述制成的土条置于渗透仓，利用膨胀土条间的空隙模拟裂隙型膨胀土，仓内壁涂满凡士林，对土体图像进行二值化处理，处理前后的图像见图2。利用PCAS软件^[25]计算土体裂隙率见图3，根据工况的不同调整土体裂隙率等参数。顶部用薄泡沫板和玻璃胶密封，防止渗漏。

图  2  二值化处理前后的土条图像

Figure  2.  Soil strips images before and after binarization processing

下载: 全尺寸图片 幻灯片

图  3  PCAS系统计算裂隙率界面图

Figure  3.  PCAS system interface for calculating fracture ratio

下载: 全尺寸图片 幻灯片

在准备工作结束后，向马里奥特瓶内注水，等到收集水桶内水开始溢出时，记录单位时间内溢出水的量。由于试验刚开始时渗透状况改变速度较大，记录时间的间隔要密一些为10 min，待到计算溢出水量变化幅度变小时，增大记录时间间隔至30 min，直至渗流稳定。

2.   初始条件对膨胀土渗透过程的影响

依据裂隙条数、宽度、长度等数据对试验进行结果概化，将25%、20%定义为高初始含水率；15%定义为中初始含水率；10%、5%定义为低初始含水率。将14%、11.5%定义为高初始裂隙率；9%定义为中初始裂隙率；6.5%、4%定义为低初始裂隙率。每组试验做5次，试验时间为660 min，取5次试验渗透系数平均值，以减小偶然误差对于渗透系数变化曲线的影响。

2.1   初始含水率对渗透系数的影响

初始含水率对膨胀土的渗流情况影响甚大，为进一步探究不同初始含水率对膨胀土渗流的影响情况，需设置不同组别试验。

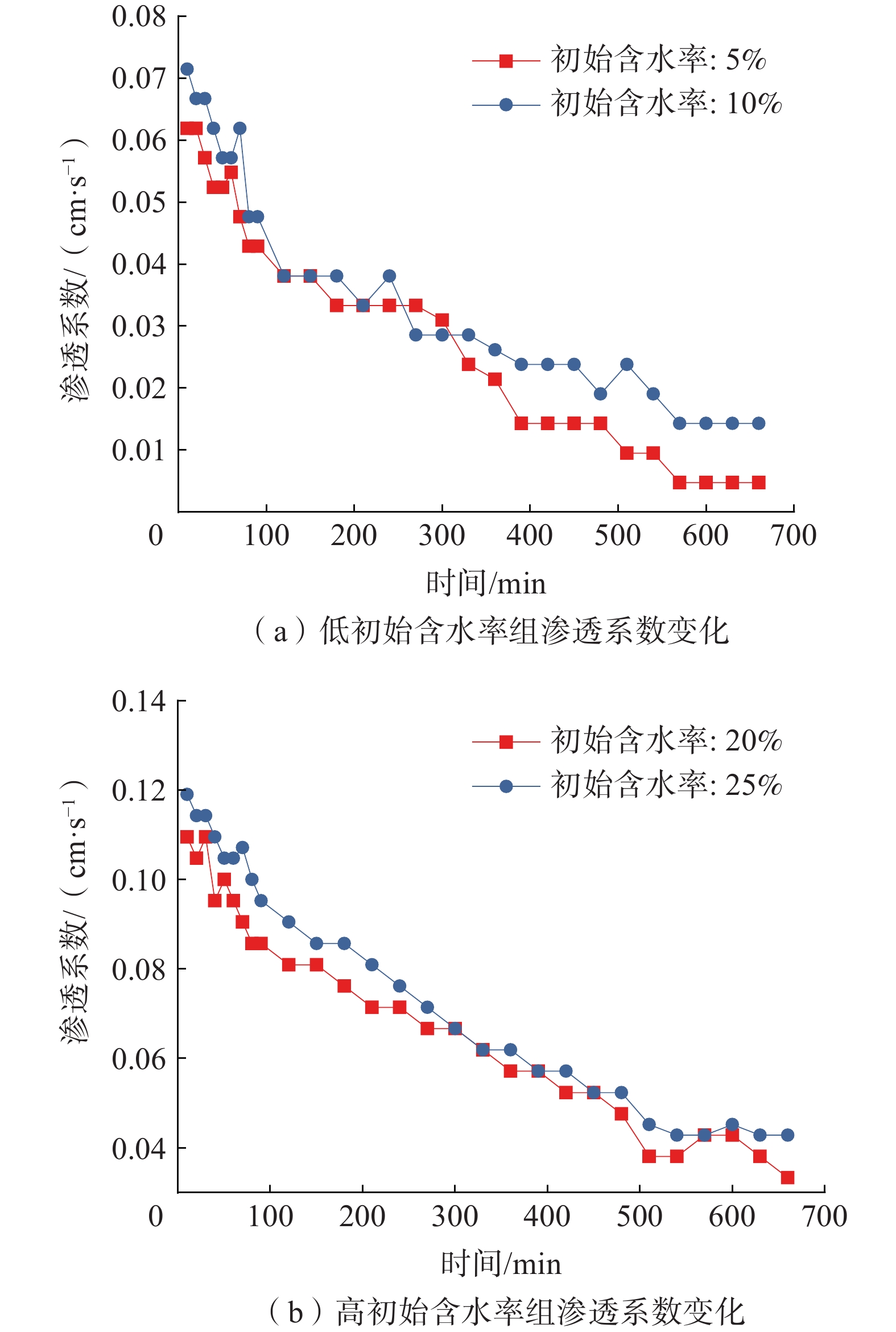
在9%初始裂隙率情况下，将初始含水率分为25%、20%、15%、10%、5% 5组，来研究初始含水率对膨胀土的渗流的影响，9%裂隙率下不同初始含水率下渗透系数变化曲线如图4所示。

图  4  不同初始含水率时渗透系数变化图

Figure  4.  Variation of permeability coefficient under different initial water content

下载: 全尺寸图片 幻灯片

对比4组不同含水率的渗透系数变化曲线，可以发现在初始裂隙率一定的情况下，土体的起始渗透系数随着初始含水率的增加而增加。这是由于初始含水率高的土体，其膨胀潜势较小，在渗流时土体的胀缩量也较小。

在裂隙率相同时，初始含水率越高，渗透系数变化幅度越小。这是由于在高初始含水率情况下，土体内部在与水接触后膨胀的程度比低初始含水率情况下要小得多，土条与土条之间裂隙闭合不充分。渗透水流在高初始含水率的土体中，仍然可以沿着尚闭合不充分的膨胀土裂隙发生渗流作用导致比低初始含水率土体的渗透系数偏大。

随着渗透时间的增长，试样的渗透系数逐渐降低并稳定在某一值，且初始含水率高的试样稳定值越高，反之则越低。这是由于土体在饱和环境的渗流作用下，已经达到能膨胀的最大值。随着初始含水率的降低，渗透系数的稳定值也在减小。这是因为初始含水率高的试样，土体内部空隙较大，在渗流过程中纵使膨胀土在不断吸水膨胀但还是无法使较大裂隙闭合，最终稳定在某一值处。从变化幅度来看，试样的初始含水率越低，变化幅度越大。当初始含水率逐渐升高时，其渗透性变化程度也在变小。由于土体在低初始含水率情况下，土体中基质吸力较大，吸收水的潜力较大。在渗流过程中不断吸水导致土体膨胀，逐渐将土条间的裂隙填满降低土体整体的渗透性。

2.2   初始裂隙率对渗透系数的影响

膨胀土初始裂隙率对土体的渗流情况影响较大，为进一步探究不同初始裂隙率对膨胀土渗流的影响情况，设置不同组别试验，在20%初始含水率和5%初始含水率情况下，将初始裂隙率分为14%、11.5%、9%、6.5%、4% 5组。

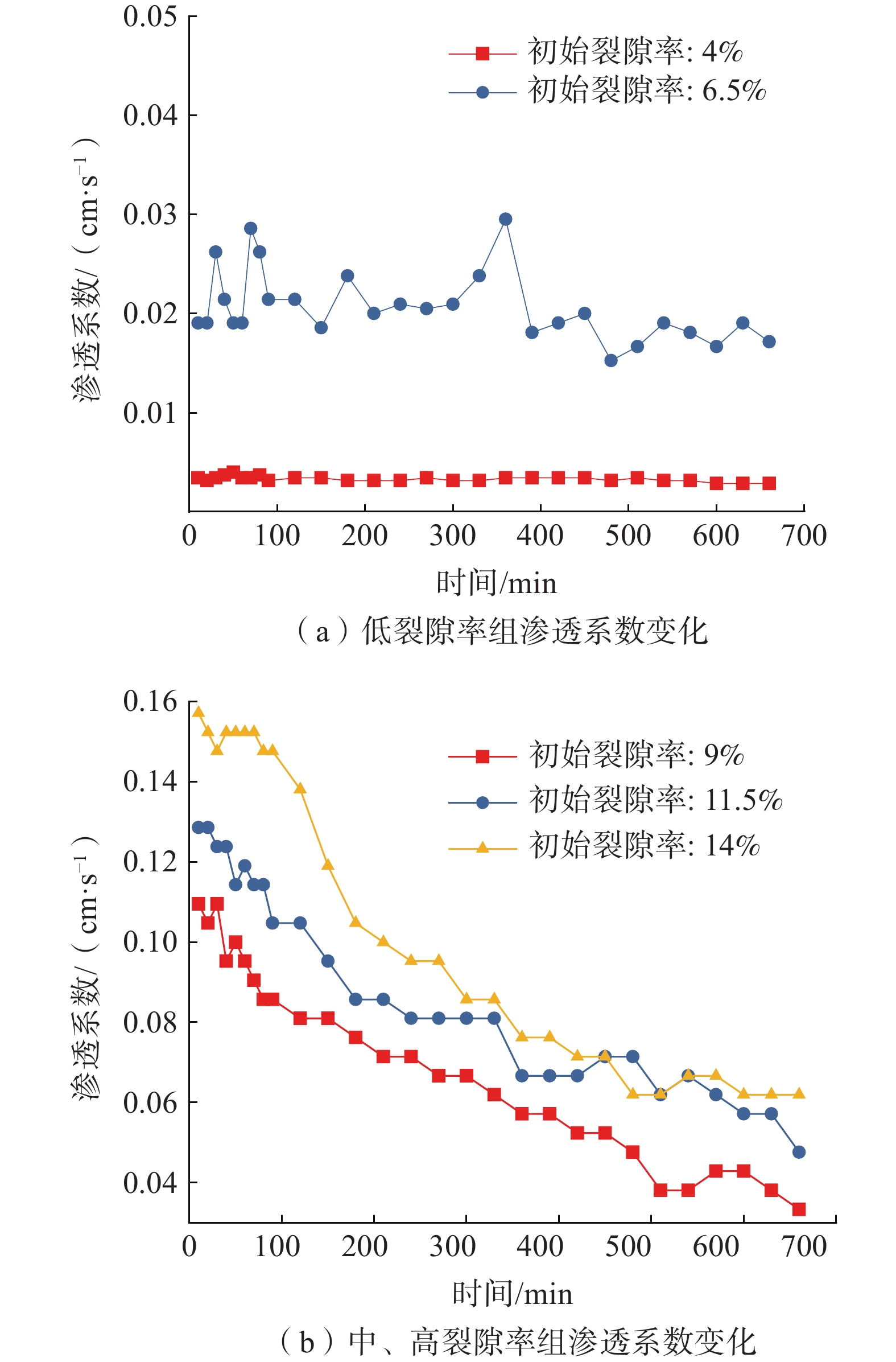
20%初始含水率的土体在不同初始裂隙率下的渗透系数变化曲线如图5所示。

图  5  不同初始裂隙率时渗透系数变化图

Figure  5.  Variation of permeability coefficient under different initial fracture ratios

下载: 全尺寸图片 幻灯片

图5（a）中初始裂隙率为6.5%的试样，5次试验得出平均渗透系数值存在波动，始终维持在2×10⁻⁴m/s；初始裂隙率为4%的试样，渗透系数一直保持3×10⁻⁵m/s。而在20%含水率情况下，裂隙型膨胀土的渗透性在低裂隙率范围内变化并不明显。由于土条间的裂隙过于狭窄，膨胀土体在高初始含水率时，发生的膨胀足以将裂缝填满，导致土体渗透系数并不发生显著变化。

而从图5（b）中可以观察到，土体的渗透系数随渗透时间的增长而变小，且随着初始裂隙率的增大，渗透系数也在增大。渗透系数变化幅度随初始裂隙率的增大而减小。中、高初始裂隙率组的土样和低初始裂隙率组的渗透系数变化有显著不同，直接影响因素为初始裂隙率。当裂隙率逐渐降低到一定值时，土体在经历渗透作用吸水后将裂隙填满，水流失去渗流通道导致土体的渗透变化不明显。在中、高初始裂隙率组中，上述过程同样存在，从图5中可见裂隙逐渐闭合，渗透系数逐渐变小。

对比不同初始裂隙率的试验可以得出土体的渗透系数随着初始裂隙率的减小而降低。初始裂隙率成为影响渗透系数的重要因素，当初始裂隙率越小，裂隙完全闭合需要的时间越短，渗透进土体内的水就越少，渗透系数也就相应的越小。

3.   渗透性变化对排水效果的影响

上述试验证明了初始含水率和初始裂隙率是引起膨胀土渗透系数变化的重要影响因素。因此可以从单因素影响和实际工况2个方面来探究膨胀土的渗透性变化过程，并进一步分析不同情况下渠坡内排水措施的排水效果。

3.1   单因素影响下渗透性变化

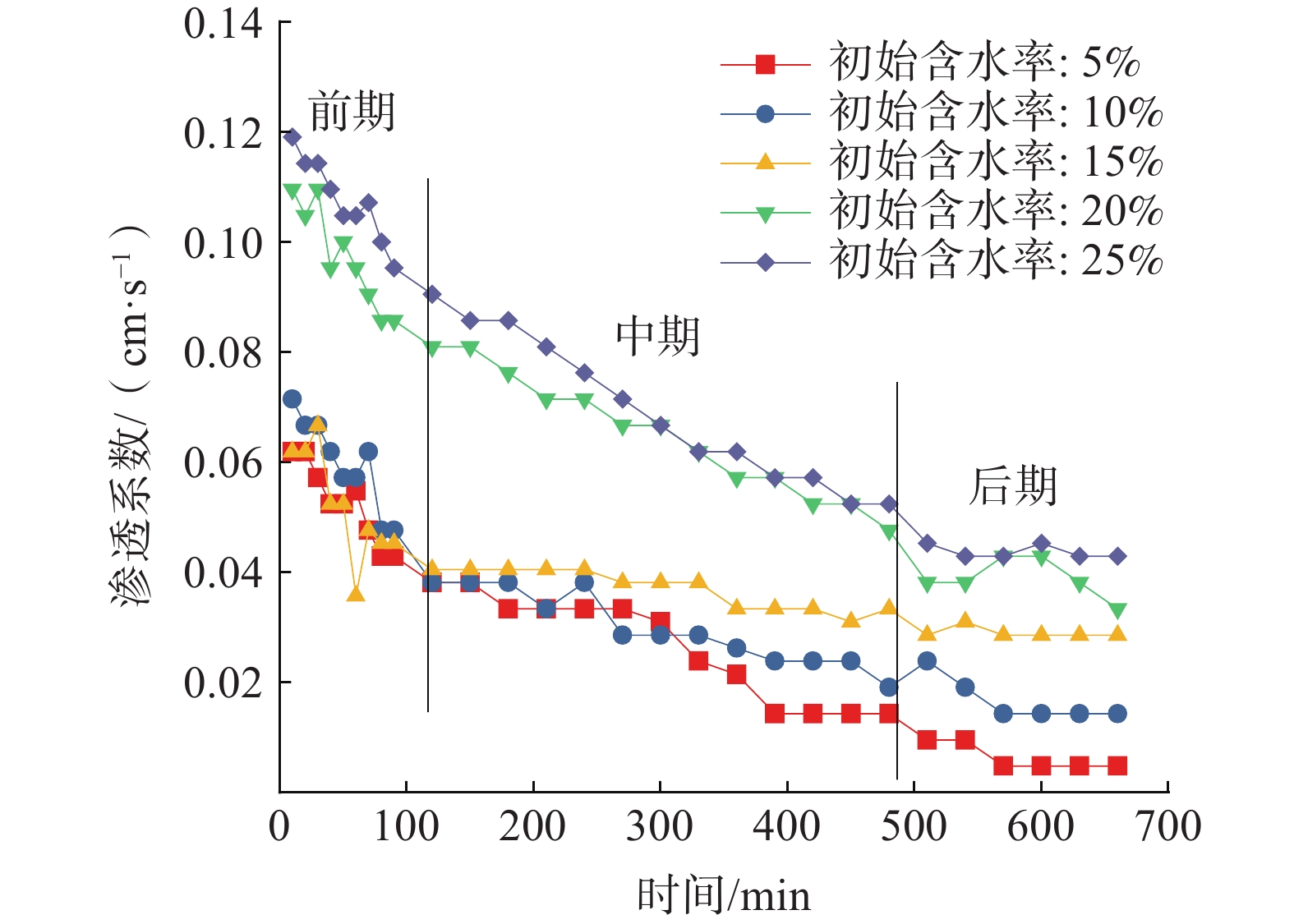
（1）在初始裂隙率一定时，研究不同初始含水率和渗透系数之间的关系。图6为初始裂隙率为9%时，不同初始含水率膨胀土渗透系数的变化过程，根据渗流过程中渗透系数的变化速率可将整个过程分为前中后期，其中前期指试验开始后2 h内，中期指2～8 h，后期指8 h后到试验结束。

图  6  9%裂隙率时渗透系数变化图

Figure  6.  Variation of permeability coefficient at 9% initial fracture ratio

下载: 全尺寸图片 幻灯片

由图6可知，渗透系数随着初始含水率的增加而增大。在渗透前期，渗透系数下降较快，在2 h左右达到最大降低速率。在实际膨胀土渠坡排水过程中这2 h极为关键，可以将水迅速从坡体内排除。在渗透中期的6 h内，土体渗透性相对较强，渗透系数降低也较明显，实际工程中应使土体中的水尽量在该阶段排出坡体，维持稳定性。

在渗流后期阶段，渗透系数变化的幅度在逐渐减小。在水的渗透作用下，膨胀土体逐渐膨胀将裂隙挤占，导致渗水通道受阻，渗透系数变小。而含水率越高，其膨胀潜力越小，土体内仍有裂隙尚未闭合，使得水有空间渗流。随着渗流作用的进行，膨胀土体逐渐吸满水分，膨胀作用减弱，导致渗透系数逐渐趋于稳定。一旦进入后续阶段，渗透性降至最低，且基本无变化，会导致排水困难。

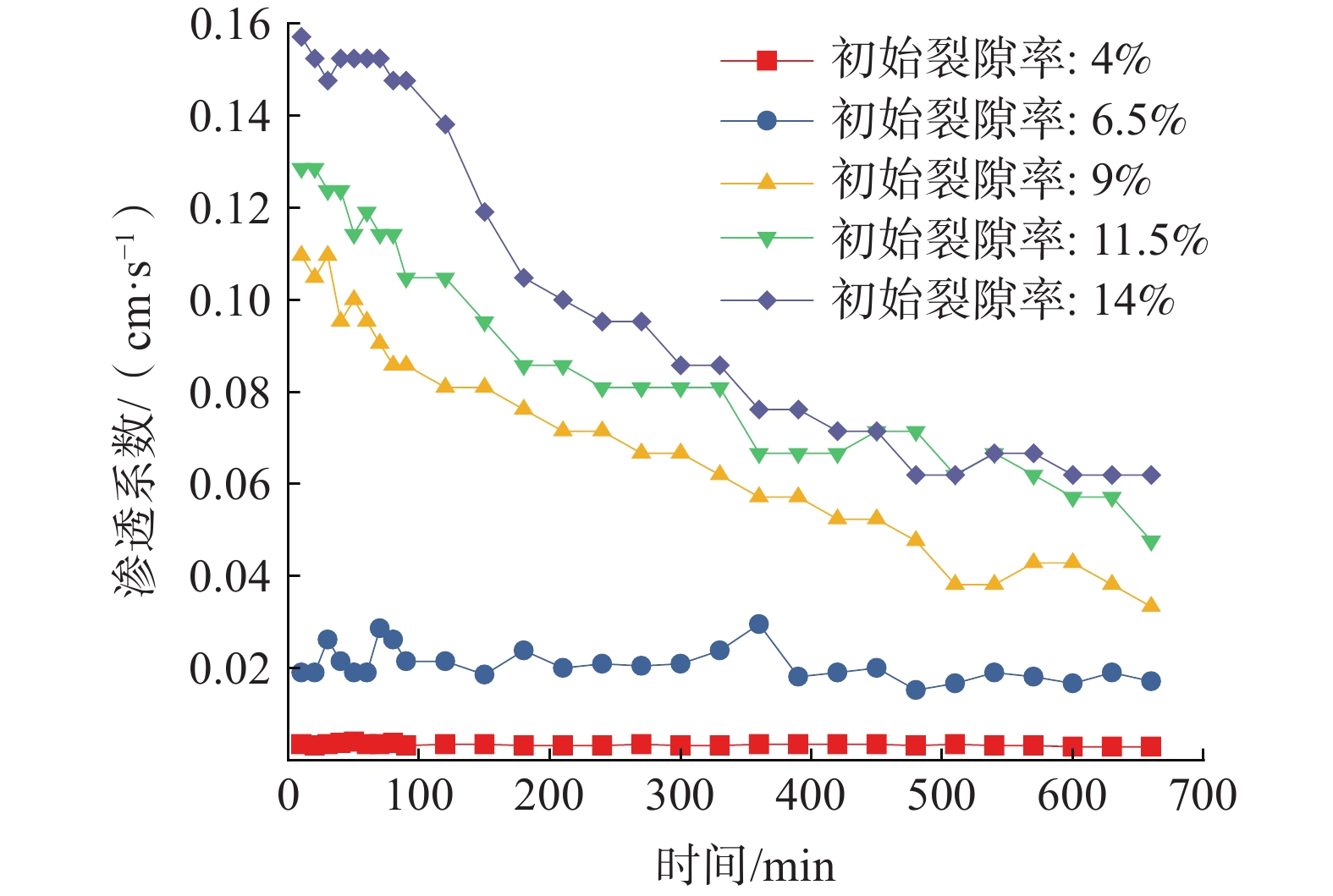
（2）在初始含水率一定时，研究初始裂隙率和渗透系数之间的关系。以20%初始含水率为例，不同初始裂隙率的试样渗透系数变化曲线见图7。

图  7  20%初始含水率时渗透系数变化图

Figure  7.  Variation of permeability coefficient at 20% initial water content

下载: 全尺寸图片 幻灯片

从图7中可以看出，与初始含水率因素影响下最大的不同是低裂隙组和中、高裂隙率的差异。在20%初始含水率条件下，低裂隙组的渗透系数变化幅度极少，但中、高裂隙组的渗透系数变化可以观察到。这主要由于，低裂隙组的土体内部裂隙比较少，在渗流作用发生后，土体膨胀裂隙闭合，导致过水不畅，渗透系数变化不明显。可推出坡体界限裂隙率在6%～9%，裂隙率低于6%的部位跟排水工程作用有限，断面应高密度设置排水设施；而裂隙率在9%以上的部分，排水工程会有效果，排水管可根据实际情况布置得稀疏。因此要根据土层初始裂隙率的大小选用不同的排水设施布置方案。

3.2   不同工况下的渗透性变化

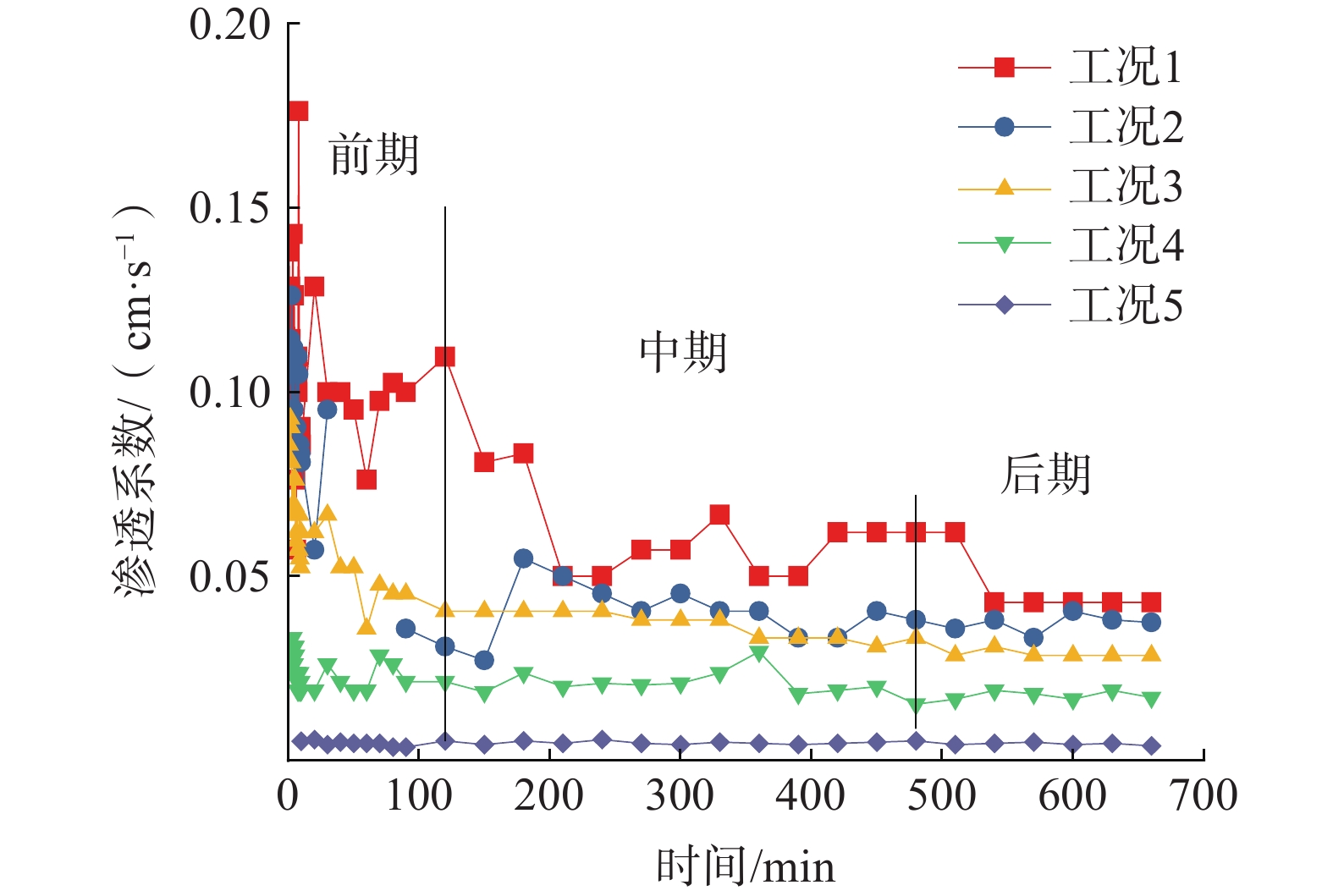
根据现场实际的工程地质状况，通过测得不同深度膨胀土含水率并将裂隙分布条件概化后得出以下数据见表2。配制以下5种工况的土样，绘制成图。5种工况的渗流变化过程如图8所示。

表  2  不同工况试验参数表

Table  2.  Experimental parameters for different working conditions

试样	初始裂隙率/%	初始含水率/%
工况1	14.0	5
工况2	11.5	10
工况3	9.0	15
工况4	6.5	20
工况5	4.0	25

下载: 导出CSV 

| 显示表格

图  8  5种不同工况渗透系数变化图

Figure  8.  Variation diagram of permeability coefficient under five different working conditions

下载: 全尺寸图片 幻灯片

在裂隙型膨胀土体内，含水率升高与裂隙闭合在渗透过程均伴随着土体同时发生的，因此试验中所测得的渗透系数实是土体基质吸力与水在裂隙内渗流的综合体现。

渗透初期，裂隙张开程度较大，水很容易地穿过试样内贯通的裂隙，这个时候裂隙内的渗流对土体渗透性的贡献极大，而基质吸力只影响土体渗透性较小部分。随着土体含水率的升高，裂隙开始闭合，裂隙内的渗流急剧下降。此阶段渗透性最强，排水设施效果最好。

在渗透中期，裂隙继续闭合，5种工况土样的渗流系数都较前期变小。由于水的渗流作用，在初期发生土体崩解的小颗粒附着在土柱间的裂隙内，造成水的渗流不畅从而降低了渗流的程度。在水的渗流过程中，土体内部不断吸水膨胀，逐渐将土体内的裂隙挤占，导致渗流不畅。土体的渗透能力下降，水分向试样内部不断渗透，也是土体不断吸水的过程，不断向饱和状态过渡。

在渗透后期，各种工况的试样的渗透系数变化均不发生明显的变化。随着时间的推移，土体内的裂隙逐渐地被淤积的土颗粒所占满。由于膨胀土吸水膨胀的特性，经过长时间的浸润作用，土体的含水率已经接近饱和状态，过水通道的数量有限，导致水只能从土体极其微小的裂隙中流进，渗透程度降到较低的水平。实际工程中排水设施排水效果有限。

4.   结论

（1）在初始裂隙率一定的情况下，土体的起始渗透系数随着初始含水率的增加而增加。初始含水率越低的土，基质吸力大，吸水后迅速膨胀导致渗透性变差，土体含水率影响着土体内裂隙的产生与发展。随着渗透时间的增长，试样的渗透系数逐渐降低并稳定在某一值，且初始含水率高的试样稳定值越高，反之则越低。

（2）排水工程在渗流的前2 h效果最好，在8 h内有一定效果，超过8 h后效果有限。由于坡体界限裂隙率在6%～9%，因此裂隙率低于6%的部位排水工程作用有限，应加大排水措施密度；裂隙率在9%以上的部分，排水工程会有效果，增设排水措施的效果更显著。

（3）根据不同深度上的初始含水率与初始裂隙率的组合特征所总结的5种工况，判断相对浅层的工况下排水效果受排水时间影响明显；而相对深层的工况，初始裂隙低、初始含水量高，渗透系数变化不明显。