Quantitative risk assessment and its application for individual landslide disaster based on slope failure probability
-
摘要:
对潜在滑坡灾害实施风险评价至关重要,但在实际工程中单体滑坡灾害风险评价仍然以定性评价方法为主,由危险性和损失通过风险矩阵得到定性风险等级,存在风险标准多重性和不连续性的问题,不便于在实际工程中对风险大小进行比较并实施分类处置,还可能导致风险评价结果出现误差,误导风险处置。为此,运用概率模型定量描述滑坡灾害的稳定性,同时考虑承灾体的损失大小,得到单体滑坡灾害风险定量评价指标,提出了滑坡灾害风险曲面及风险等值线的概念,并开发相应的评估计算软件,形成了滑坡灾害风险定量评价方法,消除了传统滑坡风险矩阵带来的风险标准多重性和不连续性,提高了评估的准确性。通过对重庆市奉节县6个单体滑坡进行风险定量评价,验证了所提方法的正确性和可靠性,为滑坡灾害风险评价提供了新的途径。
Abstract:Effective risk assessment of potential landslide disasters is crucial for informed decision-making in engineering projects. In practical engineering, the risk assessment of individual landslide disasters still relies mainly on qualitative evaluation methods. The qualitative risk level is obtained through the risk matrix based on danger and loss, which poses problems of multiple and discontinuous risk standards. This makes it difficult to compare and classify risks in actual engineering, and may also lead to errors in risk assessment results, misleading risk management. To address these issues, a probability model is employed to quantitatively describe the stability of landslide disasters, considering the size of losses to the element at risk. A quantified risk index for individual landslide disasters is obtained, introducing the concept of landslide disaster risk surface and risk contour. Corresponding evaluation and calculation software are developed to form a quantified risk assessment method for landslide disasters, eliminating the multiplicity and discontinuity of risk standards brought about by traditional landslide risk matrices. The accuracy of the evaluation is improved. By conducting quantitative risk assessment on six individual landslides in Fengjie County, Chongqing, the correctness and reliability of the quantitative risk assessment method were verified, providing a new approach for landslide disaster risk assessment.
-
0. 引言
我国西南部山高坡陡,江河众多,地质构造复杂,是地质灾害多发地区,地质灾害防治任务十分艰巨。据统计已查明的潜在地质灾害隐患中80%以上为滑坡,因此,滑坡灾害已成为最严重的地质环境问题之一[1 − 3]。数量巨大的潜在地质灾害隐患与有限的地质灾害防治人力物力之间出现了较大的差异,由此对地质灾害风险的精准评价和有效防治提出了更高的要求。如何准确地评估潜在滑坡灾害点的严重程度,如何准确判别不同滑坡灾害体的风险高低,并在此基础上有针对性地实施相应的风险处置措施已经成为地灾防治相关部门高度重视的关键问题[4 − 6]。
目前滑坡风险评价处于定性和半定量阶段,从工程应用的结果看,通常存在同一个风险等级中有多个滑坡点导致无法进行排序比较的问题,另外风险等级存在边缘突变的不合理现象,例如在低风险和高风险的边缘处一两个受威胁人员的增加或减少就会导致风险等级的变化,而在非边缘处几十个人的变化也不会产生等级的差异,这明显是不合理的。针对这些问题,提出了定量风险评价的概念和方法,运用概率模型定量描述滑坡灾害的稳定性,同时考虑承灾体的损失大小,得到单体滑坡灾害定量评价风险指标,提出了滑坡灾害风险曲面及风险等值线的概念,并开发相应的评估计算软件,形成了滑坡灾害定量风险评价方法,消除了传统滑坡风险矩阵带来的风险标准多重性和不连续性,提高了评估的准确性。为滑坡灾害风险评价提供了新的途径。
1. 滑坡灾害风险评价的传统方法
1.1 滑坡灾害的定性风险评价
根据滑坡现场地质调查收集的资料,结合专家和地质工程师的工程经验,对滑坡的稳定状态进行描述,并定性给出了相应的稳定性等级。滑坡稳定状态特征的定性描述一般包括以下几个方面[7 − 12]:(1)滑坡场地的区域地质背景;(2)滑坡的主导和诱发因素;(3)滑坡的阶段和发展趋势及可能的破坏模式。根据相关规范[13 − 14],可以对滑坡进行定性稳定性评价,并建立相应的稳定性高、中、低等级划分。类似地,潜在滑坡可能造成的损失统计通常包括以下三个方面:(1)威胁人身安全;(2)经济损失;(3)受滑坡威胁的对象的重要性(社会和经济方面)。基于以上三个方面的损失统计结果,可初步估计潜在滑坡造成的损失,并按大、中、小划分相应的损失等级。
基于风险评价的定义,结合滑坡的稳定状态和可能的损失等级,可形成一个可用于初步判断滑坡灾害风险水平的定性风险矩阵(图1)。
滑坡定性风险评价的优势在于,它是基于现场地质调查的结果,不需要测量、绘图、钻探和测试等实物工作量。它相对简单、快捷,易于在实际工程中应用。但由于缺乏详细的技术工作基础,风险影响因子的确定具有一定的主观性,相应的风险等级划分和风险水平评价结果也相对粗糙。定性风险评价适用于对大量潜在滑坡的初步筛选和比较[15],从而初选出相对的高风险滑坡体作为研判对象,实施进一步研究或评价。
1.2 滑坡灾害的半定量风险评价
为了进一步提高滑坡定性风险评价结果的准确性,可在定性风险评价中引入稳定系数,由此使得相应的风险矩阵比定性风险评价结果更为准确。
基于稳定系数的定义,滑坡稳定性分类参照《滑坡防治工程勘查规范》(GB/T 32864—2016),分类标准见表1,如表2所示保护对象的价值或潜在滑坡可能造成的损失可分为3个等级。
根据上述两个表,可以得到滑坡灾害的半定量的风险矩阵(图2),并由此来判断滑坡灾害的风险水平。
图2表明,半定量风险评价给出了具体的判断标准和划分依据,趋势正确,判别方便,适用性强。然而,由于风险区间划分的不连续性,在应用过程中仍存在一些缺陷,从而导致风险判断结果出现一些不合理现象,需要进一步改进和完善。
以滑坡的受威胁人员数量(TP)为例,参照图2所给出的风险矩阵,如果滑坡的稳定状态保持不变,即Fs为常数(Fs=1.04),则受威胁人员数量TP的变化会导致滑坡的风险水平发生以下变化(表3)。
表 3 受威胁人员数量引起的风险水平的变化Table 3. Variations in risk levels caused by the number of endangered individuals稳定系数:Fs=1.04 稳定状态:欠稳定 TP:99 等级:Ⅲ 风险水平:低 TP:101 等级:Ⅱ 风险水平:中等 TP:499 等级:Ⅱ 风险水平:中等 TP:501 等级:Ⅰ 风险水平:高 表3显示,即使Fs保持不变,TP只需增加2人(从99人增加到101人或从499人增加到501人)即可改变风险水平(从低风险到中风险或从中风险到高风险);相反,即便在同样的稳定状态下,TP增加398人(从101人增加到499人)却始终保持相同的风险水平(中风险),这显然不是一个合理的结论。
同样,以经济损失(EL)为例,即使滑坡保持在相同稳定状态(Fs=1.04),EL的变化可能会对滑坡的风险水平产生以下变化(表4)。
表 4 经济损失引起的风险水平的变化Table 4. Variations in risk levels caused by the number of endangered individuals稳定系数: Fs=1.04 稳定状态:欠稳定 EL(万元): 490 等级:Ⅲ 风险水平:低 EL(万元): 510 等级:Ⅱ 风险水平:中等 EL(万元): 4990 等级:Ⅱ 风险水平:中等 EL(万元): 5010 等级:Ⅰ 风险水平:高 表4显示,即使Fs保持不变,EL增加仅仅20万元(从490万增加到510万或从
4990 万增加到5010 万)就会改变滑坡灾害的风险水平(从低风险到中风险或从中风险到高风险);但在相同的稳定状态下,EL增加4480 万(从510万到4990 万)却不会改变滑坡灾害的风险水平(保持中风险);这也是一个不合理的结论。同样,对稳定系数也可做相同的分析。当Fs增加0.01(从1.04到1.05)时,稳定状态将从欠稳定变为基本稳定,而稳定系数增加0.1(从1.05到1.15),稳定状态却保持不变。
究其原因,主要是因为滑坡的稳定状态和保护对象价值的分类都是基于区间划分的,因此风险矩阵中存在区域内部风险的不变性和区域边缘风险的突变性,由此划分的风险等级也产生相应的不变性和突变性。解决这一问题的方法是对系统的稳定状态和保护对象进行连续描述,即用连续的分布曲线代替离散的区间划分,从而实现对风险评价的综合全定量分析。
2. 定量评价滑坡风险评价
滑坡的稳定状态和潜在损失进行定量分析是准确评价滑坡风险的必然趋势。定量评价中应充分考虑滑坡风险指标影响因素的变异性,建立其与滑坡稳定系数之间的联系。因此,相比半定性的稳定性评价方法,引入失稳概率来描述滑坡的稳定状态更合理。
根据滑坡稳定系数的定义,Fs可表示为
(1) 式中:N——抗滑力;
T——滑动力。
(2) 如将岩土材料的相关强度参数视为正态分布的随机变量,则相应的Fs也可视为随机变量。假设Fs是一个随机变量,且服从正态分布,则Fs的概率密度函数PDF(Probability density function)可以表示为[16 − 19]:
(3) 其中,x=Fs,μ=
Fs=1.0,n=0.2情况下式(3)求得的滑坡失稳概率如图3所示,失稳概率50%。
为了进一步研究Fs和n对滑坡失稳概率的影响规律,本文对不同Fs(步长0.05)和n(步长0.1)条件下的失稳概率进行了多工况计算分析,得到滑坡失稳概率P的部分计算结果如图4所示。图4中,图4(a)—(c)为稳定系数相同且小于1(Fs=0.95),变异系数不同(n=0.1,0.2,0.3)时滑坡失稳概率的变化情况;图4(d)—(f)为稳定系数相同且大于1(Fs=1.20),变异系数不同(n=0.1、0.2、0.3)时的滑坡失稳概率。
对稳定系数均值的变化也可做类似分析,对结算结果进行统计(表5—7)。
表 5 失稳概率随稳定系数的变化范围(n=0.2)Table 5. Variation range of failure probability with stability factor Fs (n=0.2)Fs 0.95 1.00 1.05 1.15 P/% 60.38 50.00 40.59 25.71 表 7 失稳概率随变异系数的变化范围(Fs=1.20)Table 7. Variation range of failure probability with coefficient of variation n (Fs=1.20)n 0.10 0.20 0.30 P/% 4.78 20.24 28.88 表 6 失稳概率随变异系数的变化范围(Fs=0.95)Table 6. Variation range of failure probability with coefficient of variation n (Fs=0.95)n 0.10 0.20 0.30 P/% 70.05 60.38 56.92 通过统计分析可知,P随Fs均值和n的变化趋势如图5所示。
从图5所反映P与Fs均值和n的相关规律可知:在均值大于1.0的区间范围内,P随n呈递增趋势;在均值小于1.0的区间范围内,P随n呈递减趋势。基于上述P的计算方法,并考虑潜在滑坡损失(C)的统计结果,可以将滑坡的风险指数(R)表示如下[20]:
(4) 依据式(4),建立了全定量风险评价概率评价模型,技术流程路线图如图6所示。
根据全定量风险评价概率模型与技术流程路线图,得到了相应的全定量的R及其随P和C变化的三维分布曲面图,(图7)和滑坡灾害风险等值线图(图8),并开发了全定量风险评价软件。
3. 滑坡评估的工程应用
为了验证全定量风险评价概率模型的准确性与可靠性,本文选取了重庆市奉节县6个不同规模滑坡的地质勘查资料,利用全定量风险评价软件进行了定量风险评价,得到了6份定量评价地灾风险评价报告,得到了针对受威胁人数(TP)以及经济损失(EL)的定量评价风险指标,并根据风险大小分类进行了排序,计算结果如表8、表9所示。其中稳定系数是规范中常用的评估方法,风险等级是目前风险评价中采用的半定量评估方法,与定量风险评价结果进行了比较:
表 8 重庆市奉节县6个滑坡的TP风险水平Table 8. Ranking of TP risk for 6 landslides in Fengjie County, Chongqing滑坡名称 分析状态 TP等级 稳定状态 失稳概率/% TP风险等级 TP风险指数 TP 风险排名 车家坝滑坡 大雨 Ⅰ 1.075
基本稳定28.52 高风险 1.589 1 火石梁滑坡 大雨 Ⅱ 1.013
欠稳定34.75 中风险 0.753 2 万家坪滑坡 大雨 Ⅱ 1.037
欠稳定31.18 中风险 0.433 3 陈家沟滑坡 大雨
高水位Ⅱ 1.069
基本稳定29.16 中风险 0.412 4 放牛坪滑坡 大雨 Ⅱ 1.065
基本稳定29.34 中风险 0.299 5 老林沟滑坡 大雨 Ⅱ 1.356
稳定11.77 低风险 0.264 6 表 9 重庆市奉节县6个滑坡的EL风险水平Table 9. Ranking of EL risk for 6 landslides in Fengjie County, Chongqing滑坡名称 分析状态 EL等级 稳定状态 失稳概率/% TP风险等级 EL风险指数 EL风险排名 车家坝滑坡 大雨 Ⅰ 1.075
基本稳定28.52 高风险 1.142 1 陈家沟滑坡 大雨
高水位Ⅱ 1.069
基本稳定29.16 中风险 1.091 2 火石梁滑坡 大雨 Ⅱ 1.013
欠稳定34.75 中风险 0.691 3 万家坪滑坡 大雨 Ⅱ 1.037
欠稳定31.18 中风险 0.570 4 放牛坪滑坡 大雨 Ⅱ 1.065
基本稳定29.34 中风险 0.293 5 老林沟滑坡 大雨 Ⅱ 1.356
稳定11.77 低风险 0.141 6 (1)根据定量评价风险指数可见,单体滑坡的风险高低不仅仅与稳定系数有关,还与受威胁人数多少或潜在经济损失大小有关。而传统评估方法的稳定系数最低的滑坡(火石梁滑坡)风险不一定最大,单体滑坡灾害的风险指数会因为滑坡稳定状态的不同、TP与EL的差异而不同,滑坡风险度是一个综合评价指标,而定量评价滑坡风险评价方法则可以给出这一指标的量化评估值,该指标可以作为滑坡灾害综合风险评价、对比分析和处置需求的重要依据,从而解决滑坡灾害风险评价中的不确定性问题,而传统的稳定系数只反映了稳定状态,而没有考虑可能的损失。
(2)采用半定量风险评价得到结果是风险等级,可见同一个风险等级中会有多个单体滑坡,就不能比较同一风险等级的单体滑坡的风险大小,而定量评价风险指标可以实现所有单体滑坡灾害风险的排序,同时从表8和表9的结果来看,定量评价指标的结果与半定量的结果是一致的,并没有出现矛盾,验证了定量评价指标的正确性,定量评价指标克服了半定量方法不能比较同一风险等级内的风险大小的缺点。
4. 结语
文章在滑坡失稳概率分析基础上,提出了滑坡定量风险评价方法,得到了滑坡定量风险评价模型,形成了定量风险评价判别技术路线。开发了相应的滑坡定量风险评价软件,得到了滑坡灾害量化风险指标变化曲面和风险等值线图。运用量化风险评价软件对重庆市奉节县6个单体滑坡进行了全定量风险评价,得到了相应的量化风险指标并与传统的稳定性评估方法和半定量评估方法进行了对比分析,验证了定量风险评价的准确性与可靠性。
定量风险评价可为滑坡地质灾害危害程度的判断提供重要的依据,在地质灾害风险管理中发挥关键的技术支撑作用,为提高地质灾害防治工作的针对性和有效性提供了可靠技术保障。
-
稳定系数(Fs) Fs<1.00 1.00≤Fs<1.05 1.05≤Fs<1.15 1.15≤Fs 稳定状态 不稳定 欠稳定 基本稳定 稳定 保护等级 Ⅰ Ⅱ Ⅲ EL/(万元) EL≥ 5000 5000 >EL≥500EL<500 TP TP≥500 500>TP≥100 TP<100 PI 非常重要 重要 一般 EL—经济损失;TP—受威胁者;PI—公共基础设施;
只要满足一个条件即可以定义为相应的保护等级表 3 受威胁人员数量引起的风险水平的变化
Table 3 Variations in risk levels caused by the number of endangered individuals
稳定系数:Fs=1.04 稳定状态:欠稳定 TP:99 等级:Ⅲ 风险水平:低 TP:101 等级:Ⅱ 风险水平:中等 TP:499 等级:Ⅱ 风险水平:中等 TP:501 等级:Ⅰ 风险水平:高 表 4 经济损失引起的风险水平的变化
Table 4 Variations in risk levels caused by the number of endangered individuals
稳定系数: Fs=1.04 稳定状态:欠稳定 EL(万元): 490 等级:Ⅲ 风险水平:低 EL(万元): 510 等级:Ⅱ 风险水平:中等 EL(万元): 4990 等级:Ⅱ 风险水平:中等 EL(万元): 5010 等级:Ⅰ 风险水平:高 表 5 失稳概率随稳定系数的变化范围(n=0.2)
Table 5 Variation range of failure probability with stability factor Fs (n=0.2)
Fs 0.95 1.00 1.05 1.15 P/% 60.38 50.00 40.59 25.71 表 7 失稳概率随变异系数的变化范围(Fs=1.20)
Table 7 Variation range of failure probability with coefficient of variation n (Fs=1.20)
n 0.10 0.20 0.30 P/% 4.78 20.24 28.88 表 6 失稳概率随变异系数的变化范围(Fs=0.95)
Table 6 Variation range of failure probability with coefficient of variation n (Fs=0.95)
n 0.10 0.20 0.30 P/% 70.05 60.38 56.92 表 8 重庆市奉节县6个滑坡的TP风险水平
Table 8 Ranking of TP risk for 6 landslides in Fengjie County, Chongqing
滑坡名称 分析状态 TP等级 稳定状态 失稳概率/% TP风险等级 TP风险指数 TP 风险排名 车家坝滑坡 大雨 Ⅰ 1.075
基本稳定28.52 高风险 1.589 1 火石梁滑坡 大雨 Ⅱ 1.013
欠稳定34.75 中风险 0.753 2 万家坪滑坡 大雨 Ⅱ 1.037
欠稳定31.18 中风险 0.433 3 陈家沟滑坡 大雨
高水位Ⅱ 1.069
基本稳定29.16 中风险 0.412 4 放牛坪滑坡 大雨 Ⅱ 1.065
基本稳定29.34 中风险 0.299 5 老林沟滑坡 大雨 Ⅱ 1.356
稳定11.77 低风险 0.264 6 表 9 重庆市奉节县6个滑坡的EL风险水平
Table 9 Ranking of EL risk for 6 landslides in Fengjie County, Chongqing
滑坡名称 分析状态 EL等级 稳定状态 失稳概率/% TP风险等级 EL风险指数 EL风险排名 车家坝滑坡 大雨 Ⅰ 1.075
基本稳定28.52 高风险 1.142 1 陈家沟滑坡 大雨
高水位Ⅱ 1.069
基本稳定29.16 中风险 1.091 2 火石梁滑坡 大雨 Ⅱ 1.013
欠稳定34.75 中风险 0.691 3 万家坪滑坡 大雨 Ⅱ 1.037
欠稳定31.18 中风险 0.570 4 放牛坪滑坡 大雨 Ⅱ 1.065
基本稳定29.34 中风险 0.293 5 老林沟滑坡 大雨 Ⅱ 1.356
稳定11.77 低风险 0.141 6 -
[1] 宋德光, 吴瑞安, 马德芹, 等. 四川泸定昔格达组滑坡灾害运动过程模拟分析[J]. 地质通报,2023,42(12):2185 − 2197. [SONG Deguang, WU Ruian, MA Deqin, et al. Simulation analysis of landslide disaster movement process in Xigeda Formation, Luding County, Sichuan Province[J]. Geological Bulletin of China,2023,42(12):2185 − 2197. (in Chinese with English abstract)] SONG Deguang, WU Ruian, MA Deqin, et al. Simulation analysis of landslide disaster movement process in Xigeda Formation, Luding County, Sichuan Province[J]. Geological Bulletin of China, 2023, 42(12): 2185 − 2197. (in Chinese with English abstract)
[2] 陶伟,胡晓波,姜元俊,等. 颗粒粒径对滑坡碎屑流动力特征及能量转化的影响——以四川省三溪村滑坡为例[J]. 地质通报,2023,42(9):1610 − 1619. [TAO Wei,HU Xiaobo,JIANG Yuanjun,et al. Influence of particle size on dynamic characteristics and energy conversion of debris flow in landslide:A case study of Sanxicun landslide in Sichuan Province[J]. Geological Bulletin of China,2023,42(9):1610 − 1619. (in Chinese with English abstract)] TAO Wei, HU Xiaobo, JIANG Yuanjun, et al. Influence of particle size on dynamic characteristics and energy conversion of debris flow in landslide: A case study of Sanxicun landslide in Sichuan Province[J]. Geological Bulletin of China, 2023, 42(9): 1610 − 1619. (in Chinese with English abstract)
[3] 张宇,徐宗恒,查玲珑,等.不同计算方法的云南省永胜县下院滑坡堰塞湖沉积物粒度特征及沉积历史重建[J/OL]. 中国地质(2022-08-22)[2023-07-12]. [ZHANG Yu,XU Zongheng,ZHA Linglong et al. [J/OL]Geology in China(2022-08-22)[2023-07-12]. http://kns.cnki.net/kcms/detail/11.1167.P.20220822.1500.018.html. (in Chinese with English abstract)] ZHANG Yu, XU Zongheng, ZHA Linglong et al. [J/OL]Geology in China(2022-08-22)[2023-07-12]. http://kns.cnki.net/kcms/detail/11.1167.P.20220822.1500.018.html. (in Chinese with English abstract)
[4] 邹凤钗,冷洋洋,陶小郎,等. 基于斜坡单元的滑坡风险识别——以贵州万山浅层土质斜坡为例[J]. 中国地质灾害与防治学报,2022,33(3):114 − 122. [ZOU Fengchai,LENG Yangyang,TAO Xiaolang,et al. Landslide hazard identification based on slope unit:A case study of shallow soil slope in Wanshan,Guizhou Province[J]. The Chinese Journal of Geological Hazard and Control,2022,33(3):114 − 122. (in Chinese with English abstract)] ZOU Fengchai, LENG Yangyang, TAO Xiaolang, et al. Landslide hazard identification based on slope unit: A case study of shallow soil slope in Wanshan, Guizhou Province[J]. The Chinese Journal of Geological Hazard and Control, 2022, 33(3): 114 − 122. (in Chinese with English abstract)
[5] 曾斌,吕权儒,寇磊,等. 基于Logistic回归和随机森林的清江流域长阳库岸段堆积层滑坡易发性评价[J]. 中国地质灾害与防治学报,2023,34(4):105 − 113. [ZENG Bin, LYU Quanru, KOU Lei, et al. Susceptibility assessment of colluvium landslides along the Changyang section of Qingjiang River using Logistic regression and random forest methods[J]. The Chinese Journal of Geological Hazard and Control,2023,34(4):105 − 113. (in Chinese with English abstract)] ZENG Bin, LYU Quanru, KOU Lei, et al. Susceptibility assessment of colluvium landslides along the Changyang section of Qingjiang River using Logistic regression and random forest methods[J]. The Chinese Journal of Geological Hazard and Control, 2023, 34(4): 105 − 113. (in Chinese with English abstract)
[6] 贾雨霏,魏文豪,陈稳,等. 基于SOM-I-SVM耦合模型的滑坡易发性评价[J]. 水文地质工程地质,2023,50(3):125 − 137. [JIA Yufei, WEI Wenhao, CHEN Wen, et al. Landslide susceptibility assessment based on the SOM-I-SVM model[J]. Hydrogeology & Engineering Geology,2023,50(3):125 − 137. (in Chinese with English abstract)] JIA Yufei, WEI Wenhao, CHEN Wen, et al. Landslide susceptibility assessment based on the SOM-I-SVM model[J]. Hydrogeology & Engineering Geology, 2023, 50(3): 125 − 137. (in Chinese with English abstract)
[7] ABEDINI M,GHASEMIAN B,SHIRZADI A,et al. A novel hybrid approach of bayesian logistic regression and its ensembles for landslide susceptibility assessment[J]. Geocarto International,2019,34(13):1427 − 1457. DOI: 10.1080/10106049.2018.1499820
[8] POURGHASEMI H R,KORNEJADY A,KERLE N,et al. Investigating the effects of different landslide positioning techniques,landslide partitioning approaches,and presence-absence balances on landslide susceptibility mapping[J]. CATENA,2020,187:104364. DOI: 10.1016/j.catena.2019.104364
[9] SHAFIZADEH-MOGHADAM H,MINAEI M,SHAHABI H,et al. Big data in Geohazard;pattern mining and large scale analysis of landslides in Iran[J]. Earth Science Informatics,2019,12(1):1 − 17. DOI: 10.1007/s12145-018-0354-6
[10] GAO Wenwei,GAO Wei,HU Ruilin,et al. Microtremor survey and stability analysis of a soil-rock mixture landslide:A case study in Baidian town,China[J]. Landslides,2018,15(10):1951 − 1961. DOI: 10.1007/s10346-018-1009-x
[11] WU Yiping,MIAO Fasheng,LI Linwei,et al. Time-varying reliability analysis of Huangtupo Riverside No. 2 Landslide in the Three Gorges Reservoir based on water-soil coupling[J]. Engineering Geology,2017,226:267 − 276. DOI: 10.1016/j.enggeo.2017.06.016
[12] YANG Beibei,YIN Kunlong,XIAO Ting,et al. Annual variation of landslide stability under the effect of water level fluctuation and rainfall in the Three Gorges Reservoir,China[J]. Environmental Earth Sciences,2017,76(16):564. DOI: 10.1007/s12665-017-6898-9
[13] 重庆市城乡建设委员会. 重庆市城市地质灾害防治工程设计规范:JTG D70—2004[S]. 重庆:2004. [Chongqing Urban Rural Development Committee E. C. S. i (2004) Code for design of geological hazard control engineering:JTG D70—2004[S]. Chongqing:2004. (in Chinese)] Chongqing Urban Rural Development Committee E. C. S. i (2004) Code for design of geological hazard control engineering: JTG D70—2004[S]. Chongqing: 2004. (in Chinese)
[14] 国家质量监督检验检疫总局,中国国家标准化管理委员会. 滑坡防治工程勘查规范:GB/T 32864—2016[S]. 北京:中国标准出版社,2017. [General Administration of Quality Supervision,Inspection and Quarantine of the People’s Republic of China,Standardization Administration of the People’s Republic of China. Code for geological investigation of landslide prevention:GB/T 32864—2016[S]. Beijing:Standards Press of China,2017. (in Chinese)] General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China. Code for geological investigation of landslide prevention: GB/T 32864—2016[S]. Beijing: Standards Press of China, 2017. (in Chinese)
[15] 解明礼,巨能攀,刘蕴琨,等,崩塌滑坡地质灾害风险排序方法研究[J]. 水文地质工程地质,2022,48(5):184 − 191. [XIE Mingli,JU Nengpan,LIU Yunkun,et. A study of the risk ranking method of landslides and collapses[J]. Hydrogeology & Engineering Geology. 2022,48(5):184 − 191(in Chinese with English abstract)] XIE Mingli, JU Nengpan, LIU Yunkun, et. A study of the risk ranking method of landslides and collapses[J]. Hydrogeology & Engineering Geology. 2022, 48(5): 184 − 191(in Chinese with English abstract)
[16] 吴越,刘东升,孙树国,等. 岩土强度参数正态–逆伽马分布的最大后验估计[J]. 岩石力学与工程学报,2019,38(6):1188 − 1196. [WU Yue,LIU Dongsheng,SUN Shuguo,et al. Maximum posteriori estimation of strength parameters for geotechnical material obeying normal-inverse Gamma distribution[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(6):1188 − 1196. (in Chinese with English abstract)] WU Yue, LIU Dongsheng, SUN Shuguo, et al. Maximum posteriori estimation of strength parameters for geotechnical material obeying normal-inverse Gamma distribution[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(6): 1188 − 1196. (in Chinese with English abstract)
[17] 盛骤,谢式千,潘承毅. 概率论与数理统计[M]. 5版. 北京:高等教育出版社,2019. [SHENG Zhou,XIE Shiqian,PAN Chengyi. Probability and mathematical statistics[M]. 5th ed. Beijing:Higher Education Press,2019. (in Chinese)] SHENG Zhou, XIE Shiqian, PAN Chengyi. Probability and mathematical statistics[M]. 5th ed. Beijing: Higher Education Press, 2019. (in Chinese)
[18] VAN DAO D,JAAFARI A,BAYAT M,et al. A spatially explicit deep learning neural network model for the prediction of landslide susceptibility[J]. CATENA,2020,188:104451. DOI: 10.1016/j.catena.2019.104451
[19] CHEN Wei,SHAHABI H,SHIRZADI A,et al. Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling[J]. Bulletin of Engineering Geology and the Environment,2019,78(6):4397 − 4419. DOI: 10.1007/s10064-018-1401-8
[20] 吴越,向灵均,吴同情,等. 基于受灾体空间概率的滑坡灾害财产风险定量评估[J]. 岩石力学与工程学报,2020,39(增刊2):3464 − 3474. [WU Yue,XIANG Lingjun,WU Tongqing,et al. Quantitative assessment of property risk of landslide disaster based on spatial probability of affected body[J]. Chinese Journal of Rock Mechanics and Engineering,2020,39(Sup 2):3464 − 3474. (in Chinese with English abstract)] WU Yue, XIANG Lingjun, WU Tongqing, et al. Quantitative assessment of property risk of landslide disaster based on spatial probability of affected body[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(Sup 2): 3464 − 3474. (in Chinese with English abstract)
-
期刊类型引用(1)
1. 朱习松,常鸣,周贤熙,赵伯驹,刘洋. 基于全连接神经网络的弥勒市域滑坡风险测度与分级评价. 防灾减灾学报. 2025(01): 8-16 .  百度学术
百度学术
其他类型引用(0)





 下载:
下载:

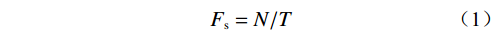

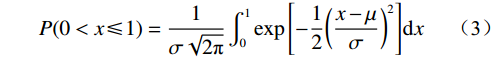
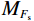
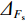
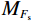
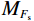
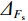



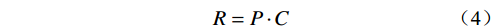



 邮件订阅
邮件订阅 RSS
RSS